非线性规划中的投影变尺度算法

王 硕，胡春燕

(1.桂林电子科技大学 数学与计算科学学院，广西 桂林 541004；2.桂林电子科技大学 电子工程与自动化学院,广西 桂林 541004)

非线性规划中的投影变尺度算法

王 硕1，胡春燕2

(1.桂林电子科技大学 数学与计算科学学院，广西 桂林 541004；2.桂林电子科技大学 电子工程与自动化学院,广西 桂林 541004)

利用投影变尺度算法，求解一类包含等式和不等式约束的一般非线性规划问题。算法基于积极集，将下降方向、可行方向、修正方向3个方向的合理组合作为算法搜索方向，且可行方向与修正方向仅需修改变尺度投影梯度方向中的部分分量。在可行集非空、问题函数2次连续可微、约束条件线性无关等条件下，证明了算法的全局收敛性和超线性收敛性。

非线性规划；投影变尺度算法；全局收敛性；超线性收敛性

考虑非线性规划问题：

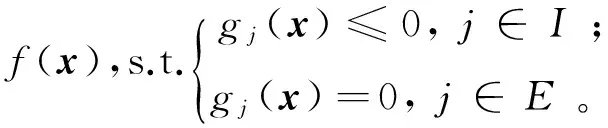
(1)

其中：I={1,2,…,m};E={m+1,m+2,…,m+l};f:Rn→R，gj:Rn→R(j=1,2,…,m+l)连续可微。式(1)的可行解集记为X。

上述非线性规划问题为包含等式和不等式约束的一般线性规划问题。这类问题在工程技术、经济、博弈论等领域都有广泛应用[1-3]，受到广泛关注。Spellucci[4]将SQP算法应用于序列等式约束2次规划问题，该方法也被称为序列等式约束2次规划问题(SECQP)算法。但其算法中相应乘子在迭代过程中不能保证非负性，同时也存在其他缺点。朱志斌[5]针对这些问题，提出了修正的SQP算法，但是，其算法每次迭代计算量仍然很大。为此，提出一种非线性规划中的投影变尺度算法，以减少计算量。

1 投影变尺度算法

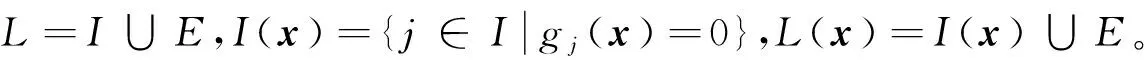
minFc(x), s.t.gj(x)≤0,j∈L。

(2)

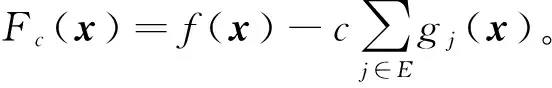
X+={x∈Rn|gj(x)≤0,j∈L=I∪E}。

作如下假设：

H1 式(1)、(2)的可行解集非空，即X≠∅,X+≠∅。

H2 函数f(x)、gj(x)(j∈L)至少2阶连续可微。

H3 对∀x∈X+,向量组{gj(x),j∈L(x)}线性无关。

1)计算：

2)令i=i+1,εk,i=εk,i-1/2，转步骤1)。

3)计算：

Ak=A(xk)=(gj(xk),j∈Jk),

πk=π(xk)=-Bkf(xk)。

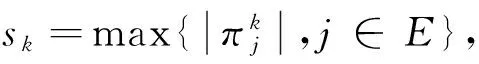
4)计算：

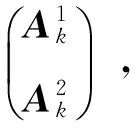
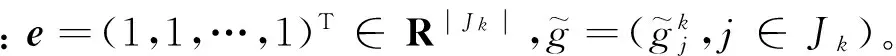
则令λk=1，转步骤9)。

7)计算ρk=-通过求解线性方程组‖‖e,得；与一样，组合≜保证成立。建立如下凸组合：

其中

(5)

8)作非精确线搜索，求满足

(6)

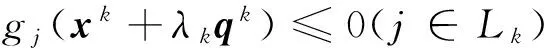
9)采用BFGS公式或DFP公式修正Hk+1，并且

令xk+1=xk+λkdk,k=k+1，返回步骤1)。

2 全局收敛性

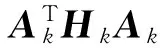
H5 存在常数b≥a>0,使得∀k∈R,∀y∈Rn，有

a‖y‖2≤yTHky≤b‖y‖2。

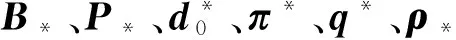
引理1 对任意迭代指标k,本算法中步骤1)迭代次数有限。

由文献[5]，易证以下定理1、2。

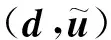
引理2 对本算法，有以下结论成立：

2)若xk不是式(1)的KKT点，则有

且存在常数c0>0,使得Fc(x)Tqk≤-c0‖qk‖2。

证明 1)经过简单的推导易知

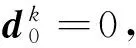
基于2005年、2008年、2011年、2014年以及2017年各年度内南充市各景区交通道路数量、车流量以及实验测试数据，以南充市20国家级旅游景区为例，对景区交通可达性进行定量化分析和计算，探讨了影响景区交通可达性的关键因素，基于关键影响因素提出景区可达性的具体意见和优化策略，以便更好地促进南充市旅游资源开发利用和旅游业快速发展。

由Hk的定义有：

f(xk)+Akγ=0,γj≥0；

γjgj(xk)=0,j∈Jk。

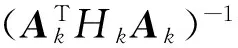
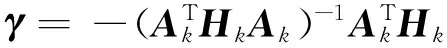
易知

αk=0,Hkf(xk)-HkAkBkf(xk)=0,

即Pkf(xk)=0，所以

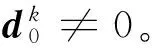
-f(x)TPk

-(Pk

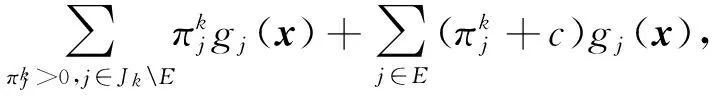
由式(4)知τk∈(0,1]，因此有

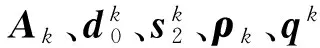
结论2)得证。

引理3 存在正整数k0，使得

ck≡ck0≜c,∀k≥k0。

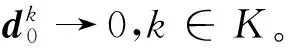
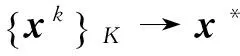
Fc(xk)→Fc(x*)，k→。

(7)

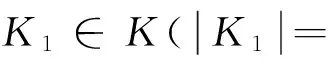
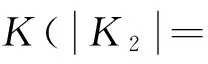
gj(x*)Tq*<0，j∈I(x*)∪E。

当k充分大时,

对于步骤8)产生的λk，易证λk≥λ*=inf{λk,k∈K}>0，k∈K；又根据式(7)得，

根据引理4，可得算法的全局收敛性。

对本算法中的x*及其对应的KKT乘子μ*，作以下假设。

H6 2阶充分条件及严格互补条件成立。

类似文献[6]中的引理4.1，有以下结论。

定理4 若H4～H6成立，则有

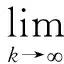
‖xk+1-xk‖=0,

3 超线性收敛性

H7Hk→H*,k→。

引理5 1)当k充分大时，Jk≡L(x*)=L*。

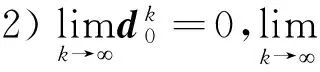
引理6 1)记

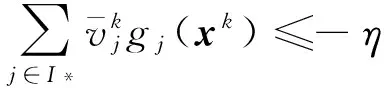
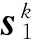
故存在η>0，使

2)由

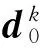
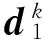
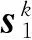
证毕。

为证明超线性收敛，作如下假设。

其中：

引理7 当k充分大时，

利用文献[8]中定理5.2可得到以下收敛性结果。

定理5 本算法超线性收敛，即

‖xk+1-x*‖=o(‖xk-x*‖)。

4 结束语

基于一个积极集策略，将投影变尺度算法应用到一类包含等式和不等式约束的一般非线性规划问题。投影变尺度算法利用下降方向、可行方向、修正方向3个方向的合理组合作为算法中的搜索方向，减少了计算量。在可行集非空、问题函数2次连续可微、约束条件线性无关等条件下，证明了算法的全局收敛性和超线性收敛性。

[1] 高自友，贺国平.约束优化问题的一个广义梯度投影法[J].科学通报，1991,36(19):1443-1447.

[2] 赖炎连，贺国平，高自友.非线性最优化的广义梯度投影法[J].中国科学，1992(9):916-924.

[3] 简金宝，张可村.不等式约束优化一个具有强收敛的强次可行方向法[J].西安交通大学学报:自然科学版，1999,33(8):88-91.

[4]SpellucciP.AnSQPmethodforgeneralnonlinearprogramsusingonlyequalityconstrainedsubproblems[J].MathematicsProgram,1998,82(1):413-448.

[5]ZhuZhibin,ZhangWeidong,GengZhenjie.AfeasibleSQPmethodfornonlinearprogramming[J].AppliedMathematicsandComputation,2010(215):3956-3969.

[6]ZhuZhibin.AgloballyandsuperlinearlyconvergentfeasibleQP-freemethodfornonlinearprogramming[J].AppliedMathematicsandComputation,2005(168):519-539.

[7] 朱志斌.一个新的共轭投影梯度算法及其超线性收敛性[J].应用数学学报，2004,27(1):149-161.

[8]FacchineiF,LucidiS.Quadraticlyandsuperlinearlyconvergentforthesolutionofinequalityconstrainedoptimizationproblem[J].JOTA,1995,85(1):265-289.

编辑：翁史振 见习编辑：陈汝伟

Project variable metric algorithm for nonlinear optimization

Wang Shuo1, Hu Chunyan2

(1.School of Mathematics and Computational Science, Guilin University of Electronic Technology, Guilin 541004, China;2.School of Electronic Engineering and Automation, Guilin University of Electronic Technology, Guilin 541004, China)

To solve nonlinear optimization with equality constraints or inequality constraints, an improved project variable metric algorithm is proposed. Based on an active set strategy, the direction is combined with the descent direction, the feasible direction and the revised direction. Part of the direction is combined with the feasible direction and the revised direction. In conditions that feasible sets are nonempty, the functions of problem are twice continuously differentiable, the vectors of constraints are linearly independent, global convergence and superlinear convergence of the proposed algorithm is proved.

nonlinear optimization; project variable metric algorithm; global convergence; superlinear convergence

2015-03-17

国家自然科学基金(11361018)；广西自然科学基金(2014GXNSFAA118010)；广西信息科学实验中心开放基金(20130103)；桂林市科学研究与技术开发计划(20140127-2)

胡春燕(1975-)，女，湖南双峰人，讲师，研究方向为最优化及其应用。E-mail:huchyel@guet.edu.cn

王硕，胡春燕.非线性规划中的投影变尺度算法[J].桂林电子科技大学学报，2015,35(3):250-254.

O224

A

1673-808X(2015)03-0250-05