杂波环境下基于粒子滤波的雷达微弱目标TBD算法

闫青竹，吴孙勇，蔡如华，谢兴祥

(桂林电子科技大学 数学与计算科学学院，广西 桂林 541004)

杂波环境下基于粒子滤波的雷达微弱目标TBD算法

闫青竹，吴孙勇，蔡如华，谢兴祥

(桂林电子科技大学 数学与计算科学学院，广西 桂林 541004)

针对杂波环境下的雷达微弱目标检测前跟踪问题，提出了Weibull杂波分布下PF-TBD算法。该算法采用Weibull杂波分布的量测模型，并基于粒子滤波算法，推导出似然函数和粒子权重。仿真结果表明，Weibull杂波环境下PF-TBD算法稳定性良好。

杂波；威布尔分布；粒子滤波；检测前跟踪；微弱目标

雷达弱目标检测一直是信号处理中的难题，检测前跟踪(track-before-detect，简称TBD)是低信杂噪比(signal-to-clutter-noise ratio，简称SCNR)下对目标进行处理的一种多帧信号积累方法，而粒子滤波(particle filter，简称PF)方法非常适合处理这类问题。Rollason等[1]在2001年第一次明确提出PF-TBD的概念，并将该方法应用于凝视型光电传感器的单目标检测与跟踪处理中。2004年，Rutten[2]提出了一种针对观测噪声为Rayleigh情形下的EPF-TBD算法。此后，Salmond将PF-TBD应用于Gaussian观测噪声背景、幅度未知的点目标场景，实现对目标幅度的估计。Boers和Driessen[3-4]研究了2个目标的PF-TBD，并将该方法应用于扩展目标的检测前跟踪。Clark等[5]将基于随机集理论的PHD滤波引入到多目标TBD算法中。Morelande等[6]和Sabahi等[7]讨论了多目标多模型粒子滤波，并将该方法应用于红外弱小目标的探测。李翠芸等[8]在粒子滤波器中运用迭代EKF、遗传算法的思想。Su等[9]在超视距雷达目标检测中运用Rao-Blackwellised。王首勇等[10]提出了PF-LR方法，并运用于Swerling II起伏目标模型中。

但上述方法只考虑Gaussian噪声下的微弱目标检测问题，未充分考虑杂波情况。当雷达工作于下视状态时，经STAP技术抑制后的量测数据除了噪声还受剩余杂波的影响，使得传统基于噪声假设的量测模型不准确。同时，随着雷达性能的改善，研究者发现地(海)杂波出现了很长的波动，其杂波的统计特性明显偏离Gaussian。为了更准确地符合实际回波的统计特性，雷达地(海)杂波一般采用非Gaussian模拟。当高分辨雷达处于低地面作业时，通过考察地(海)杂波发现，Weibull分布在一定程度内与杂波信号的幅度吻合[11]。因此，用Weibull描述实际环境中的杂波意义很大。

鉴于此，引入杂波模型信息建立更精确的传感器量测模型，并基于粒子滤波算法，推导出似然函数和粒子权重，实现对目标的检测与跟踪。

1 系统模型的建立

1.1 目标状态模型

为了简化实际环境中雷达复杂多变的状态，设目标运动模型为：

xk=fk-1(xk-1)+ωk-1。

(1)

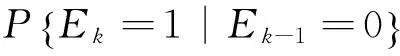
1.2 量测模型

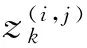
(2)

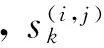
(3)

(4)

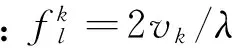
(5)

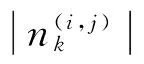
(6)

其中：p为形状参数；q为尺度参数。

2 杂波环境下基于粒子滤波的TBD算法

(7)

(8)

(9)

(10)

其中，Ci(xk)和Cj(xk)为受信号强度影响的(i,j)集合。

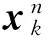
(11)

(12)

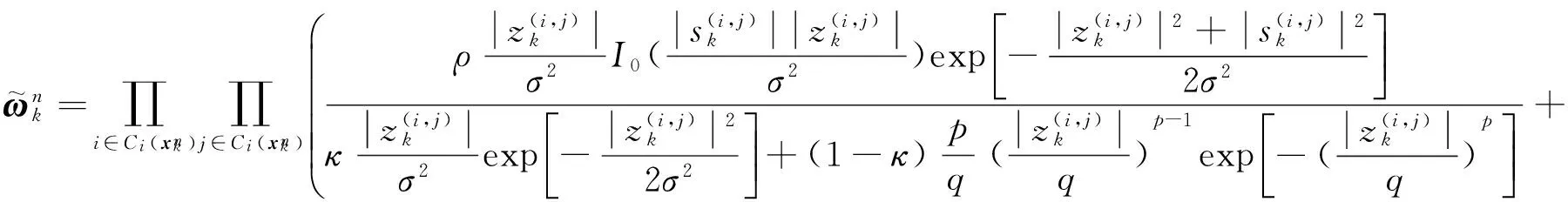
(13)

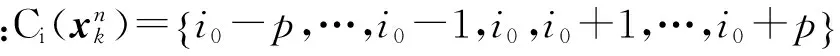
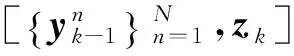
forn=1∶N

Endfor

(14)

估计目标状态，可得

(15)

3 仿真试验

研究单个目标的运动情况，假设该目标作匀加速运动，过程噪声为Gaussian白噪声，且观测噪声满足Gaussian分布，运动模型为：

(16)

式中：

(17)

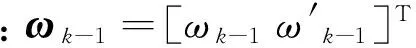
(18)

其中：PS为信号功率；PC为杂波功率；PN为噪声功率。

目标pb和pd均取为0.05，初始状态μ1=0.1，距离状态r～U[0,n]，速度状态v～U[-vmax,vmax]，加速度状态a～U[-amax,amax]。其中，v=2000m/s，amax=120m/s2，p=2，Weibull分布中预设参数p′=4，q=2。权重ρ=0.95，κ=0.95(权重ρ、κ可根据实际情况选取，一般情况下，杂波值应略低于信号值)。

MonteCarol模拟统计次数取100。图1为RSCN=6dB时，采用含杂波情况下的PF算法时距离的均方根误差(root-mean-squareerror，简称RMSE)与N的关系。随着粒子数的增加，RMSE逐渐减小，但当粒子数到达一定数目时，RMSE改善已达到稳定期。为了平衡算法的计算精度与效率，仿真均假设粒子数N=10 000。

图1 当RSCN=6 dB时，目标距离的RMSEFig.1 RMSE of target distance when RSCN=6 dB

考察杂波环境下的2种滤波算法，在杂波情况下，第1种方法(TBD-PF1)，粒子滤波采用传统的似然函数以及似然比，未加入杂波因子；第2种方法(TBD-PF2)为本算法，即在似然函数和似然比中加入杂波因子，并改进粒子滤波算法。

图2为RSCN=6dB和RSCN=3dB时的检测概率Pk值。将门限设为0.6，从图2(a)可见，TBD-PF2算法和TBD-PF1算法均能检测并跟踪目标。TBD-PF2检测的可靠性比较高，但目标有1个延时，而TBD-PF1稍微差一点，目标有3个延时，但两者均能准确判断目标消失时间。

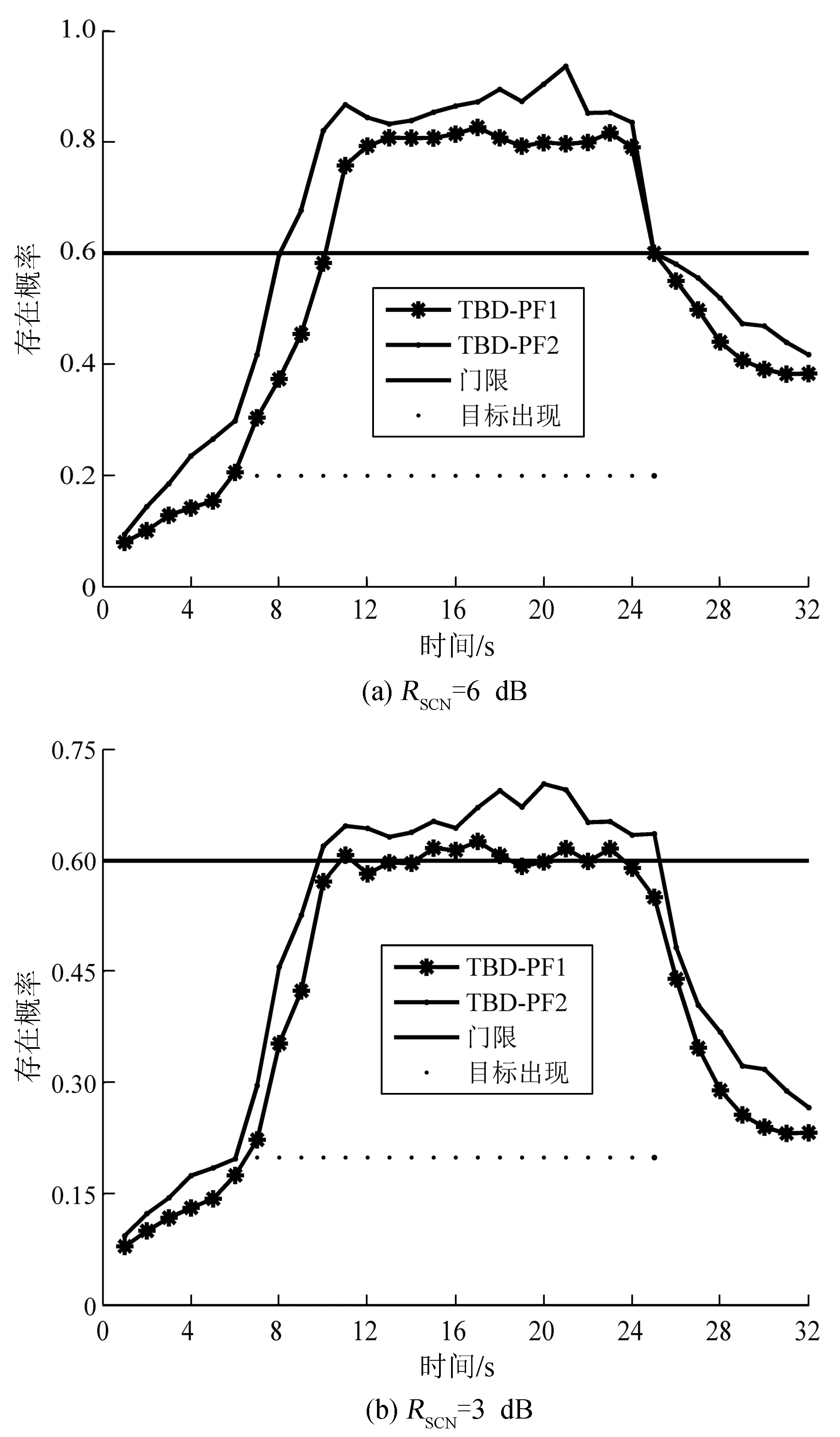
图2 目标存在概率Fig.2 Probability of target existence

在RSCN=6dB情况下，图2(b)中的TBD-PF2在目标出现的初期有2个延时，而TBD-PF1目标出现时有3个延时，TBD-PF2能准确发现目标消失，TBD-PF1目标消失时有1个漏警。从整体情况来看，RSCN=3dB时，2种算法所得目标存在概率均略差于RSCN=6dB。

图3为目标的检测概率，从图3可看出，TBD-PF2算法与TBD-PF1算法的检测概率与RSCN成正相关，但TBD-PF2算法在不同RSCN的检测效果均优于TBD-PF1算法，当RSCN=6dB时，TBD-PF2算法的Pk可达到0.8。

图3 目标的检测概率Fig.3 Probability of target detection

4 结束语

针对杂波环境下的雷达微弱目标检测问题，提出Weibull杂波环境下雷达微弱目标PF-TBD算法，通过建立杂波模型，并在PF的基础上，推导出似然函数和粒子权重，实现对目标的检测与跟踪。下一步工作可考虑改进算法，使其能够更精确地检测雷达微弱目标，同时考虑杂波环境下基于粒子滤波的雷达扩展目标检测前跟踪算法。

[1]RollasonM,SalmondDJ.Aparticlefilterfortrack-before-detectofatargetwithunknownamplitude[J].IEEDigest,2001,3(4):36-41.

[2]RisticB,ArulampalamS,GordonN.BeyondtheKalmanFilter:ParticleFiltersforTrackingApplication[M].Boton-London:ArtechHouse,2004:236-269.

[3]BoersY,DriessenJN.Aparticle-filter-baseddetectionscheme[J].IEEESignalProcessingLetter,2003,10(10):300-302.

[4]BoersY,DriessenJN.Multitargetparticlefiltertrackbeforedetectapplication[J].IEEProceedings-Radar,SonarandNavigation, 2004, 151(6):351-357.

[5]ClarkDE,BellJ.Multi-targetstateestimationandtrackcontinuityfortheparticlePHDfilter[J].IEEETransactiononAerospaceElectronSystems,2007,43(4):1441-1443.

[6]MorelandeMR,KreucherCM,KastellaK.Abayesianapproachtomultipletargetdetectionandtracking[J].IEEETransactionsonSignalProcessing,2007,55(5):1589-1604.

[7]SabahiMF,HashemiMM,SheikhiA.RadardetectionbasedonBayesianestimationoftargetamplitude[J].IETRadar,SonarandNavigation,2008,2(6):458-467.

[8] 李翠芸，姫红兵.新遗传粒子滤波的红外弱小目标跟踪与检测[J].西安电子科技大学学报：自然科学版，2009,36(4):619-623.

[9]SuHT,WuTP,LiuHW,etal.Rao-blackwellisedparticlefilterbasedtrack-before-detectalgorithm[J].IETSignalProcessing,2008,2(2):169-176.

[10] 王首勇，于兴伟.一种基于粒子滤波的雷达目标似然比检测方法[J].电子学报，2010,38(3):503-506.

[11] 郑建军，吕世芳.相关Weibull分布雷达气象杂波模拟[J].微计算机信息，2011,27(9):210-212.

[12]AbrahamDA,GelbJM,OldagAW.Backgroundandcluttermaxturedistributionsforactivesonarstatistics[J].IEEEJournalofOceanicEngineering,2011,36(2):231-247.

[13] 吴孙勇，廖桂生，杨志伟.基于改进粒子滤波的微弱目标检测前跟踪算法[J].系统工程与电机技术，2010，32(9)：1875-1879．

编辑：梁王欢

TBD algorithm of the weak target based on particle filter in the clutter environment

Yan Qingzhu, Wu Sunyong, Cai Ruhua, Xie Xingxiang

(School of Mathematics and Computational Science, Guilin University of Electronic Technology, Guilin 541004, China)

To detect and track the weak target of radar in the clutter environment, PF-TBD algorithm is presented in the clutter of Weibull distribution. The algorithm uses a measurement model in the clutter of Weibull distribution based on particle filter and derives likelihood function and particle weights. Simulation results show that PF-TBD algorithm in the clutter of Weibull distribution is stable.

clutter; Weibull distribution; particle filter; track-before-detect; weak target

2014-12-16

国家自然科学基金(61261033,41201479,61062003,61162007)；广西自然科学基金(2013GXNSFBA019270)；广西无线宽带通信与信号处理重点实验室主任基金(12102)；桂林电子科技大学研究生教育创新计划(GDYCSZ201431)

吴孙勇(1981-)，男，广西桂林人，副教授，博士，研究方向为微弱目标检测、粒子滤波。E-mail:wsy121991@guet.edu.cn

闫青竹，吴孙勇，蔡如华，等.杂波环境下基于粒子滤波的雷达微弱目标TBD算法[J].桂林电子科技大学学报，2015,35(3):202-206.

TN957.52

A

1673-808X(2015)03-0202-05