基于自适应粒子群优化的SV M算法在建筑物沉降预测中的应用

张潇珑

（江西信息应用职业技术学院 环境工程系，江西 南昌330043）

建筑物沉降预测有多种方法，包括回归分析法、灰色理论法、时间序列法、人工神经网络法。以上几种方法存在周期长、速度慢、误差大等缺点，在样本数目较大的条件下能取得良好的预测效果，但在小样本数目的预测方面取得的成效并不理想。灰色理论法在建筑物沉降过程中受到的影响较大，精度得不到保证。人工神经网络在计算时存在收敛慢等现象，预测效果往往达不到要求。支持向量机［1］在实际应用中存在一个亟待解决的问题，即对于算法中的某些参数应该如何设置。

针对这一问题，本文提出自适应粒子群优化的支持向量机算法，利用自适应粒子群优化算法改进支持向量机的参数选择和设置，解决在建筑物变形预测方面的难题。

1 自适应粒子群优化算法

粒 子 群 算 法［2］（Particle Swar m Optimization，PSO）是一种人工智能算法，其基本思想来源于对鸟群觅食过程的模拟和研究，是Eberhart于1995年提出的一种群体性、自适应型的算法。近几年，PSO算法的研究热点逐渐倾向于它的全局收敛性、收敛精度及最优解的确定。群体中的鸟被理想化为“粒子”，它们在运动的过程中会受到速度和自身位置的影响，最终在复杂的空间里找出最优解 因此PSO算法 核心部分由速度和位置两个方面构成。

在n维空间中，设有粒子群搜索，该种群由m个粒子构成：Q＝｛Q1，Q2，…，Qm｝，每一个粒子所处的位置Qi＝｛qi1，qi2，…，qin｝，每一个粒子的速度可记为：Vi＝｛vi1，vi2，…，vin｝。则每个粒子的速度和位置可表示为

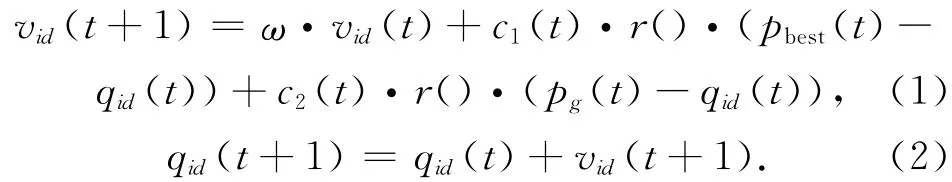
式中：vid（t＋1）表示第i个粒子在t＋1次迭代中，在第d维中的速度；c1（t），c2（t）为加速常数；r（）为区间［0 ，1］上的随机数；pbest为个体粒子最佳位置；pg为整个种群中的最优位置；ω表示惯性权重，可根据式（3）进行迭代法计算。

式中：ωmax为起始值；ωmin为终止值；itermax表示最大迭代次数；iter为当前迭代次数。

为避免算法进入早熟状态，在算法中引入变异算子，具体方法是在一定区域内，粒子与粒子间的距离要找到一个平衡点，即保持粒距在一定的精度后，保留平衡点所在的最优位置，重新开始在空间区域内的下一步搜索。因此，分别将速度算式和位置算式改为式（4）、式（5）。

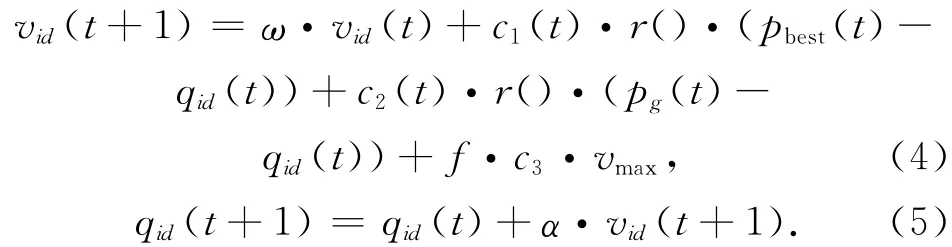
式（4）中，在式后加入的一个部分f·c3·vmax即为变异算子，当某个粒子进入局部收敛时，对飞行速度的变异；f作为一个标志值，取值范围为0或1，一般情况下为0，当陷入早熟时取值为1，c3为加速常数，可由式（6）定义。

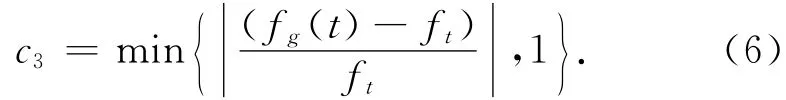
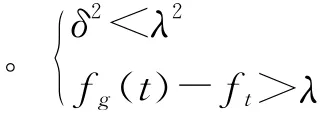
以上设计的方法，自动调整粒子在搜索区域内的搜索方向、速度、位置的功能称之为自适应粒子群优化算法（APSO）［4］，算法流程如图1所示。

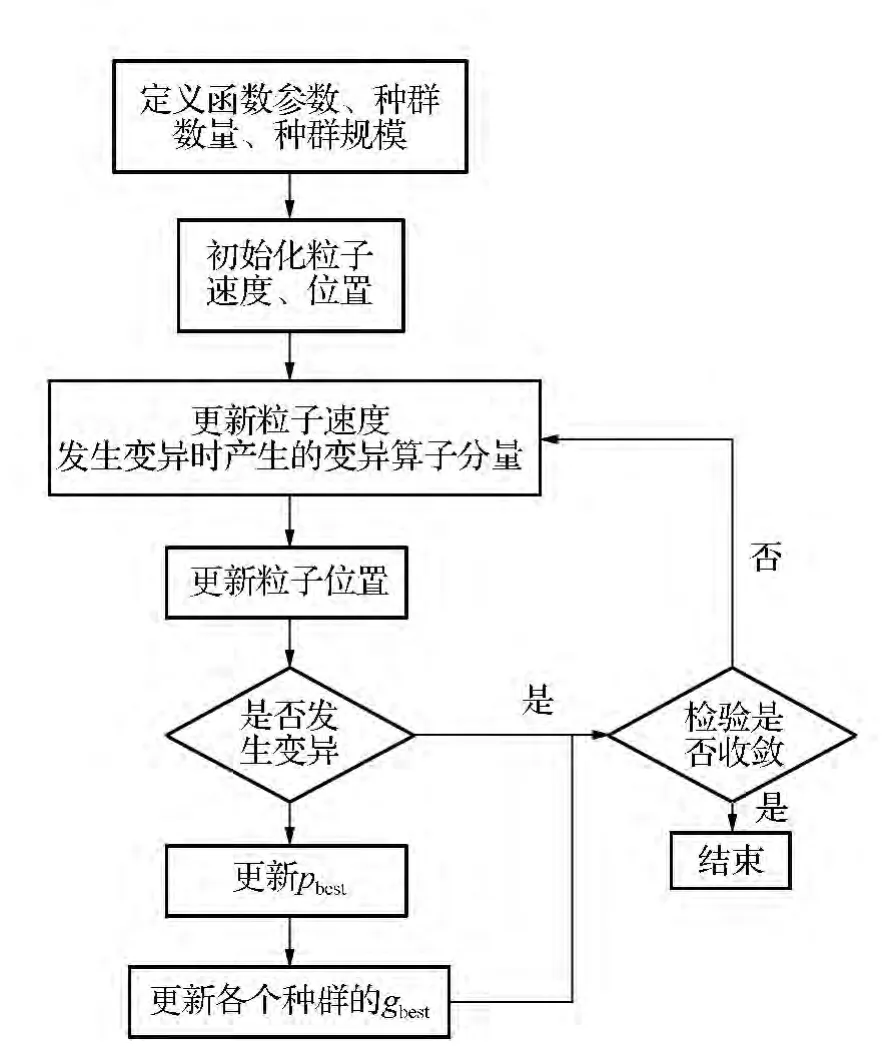
图1 APSO算法流程图

2 自适应粒子群优化的支持向量机算法

本文将自适应粒子群优化的支持向量机算法称之为APSO－SVM算法。针对于支持向量机，主要是其核函数及模型参数的确定。核函数类型主要包括：线性核函数、多项式核函数、径向基核（RBF）、傅里叶核函数、样条核函数、Sigmoid核函数。在选取最优核函数时，相对误差最小的核函数就是最优核函数。在一般情况下，选择线性核函数为最优选择。

对于模型参数，APSO算法将对SV M的部分参数进行优化和选取。模型参数包括惩罚因子（γ）、核函数（σ）、不敏感损失系数（ε）［5］，得到APSO－SV M算法预测模型的建立步骤如下：

Step 1建立数据集并进行数据预处理。根据训练样本及数据空间结构，构建合适的数据集，将集合内的数据进行预处理。

Step 2 APSO参数初始化。包括的参数设定为：种群规模scale及范围scope、加速常数c1和c2、进化代数最大值Tmax、惯性权值因子maxω和minω、粒子初始位置S及初始速度v1，v2，…，vm，m表示种群大小。

Step 3评价种群m（t）。

Step 4计算粒子群的适应度方差δ2。

Step 5根据式（4）、式（5）更新粒子的速度及位置，最优位置为pbest，根据式（3）更新粒子的惯性权重ω，生成新的种群m（t＋1）。

Step 6检查最优解条件 判断适应度值是否满足最大迭代次数，如果满足，则寻优结束，输出最优值best（γ，σ，ε）。如果不满足条件，则转至Step2，继续寻优。

Step 7找到粒子的最优位置及速度后，将输出的最优参数best（γ，σ，ε）赋给SV M算法中进行训练学习。

Step 8将训练过的样本数据输入到SV M网络中［6］，对SV M进行训练，得到预测模型，进行预测。

APSO算法过程通过Apsopr ogress实现，部分代码如下：

%适应度的计算：

Apso＝［v，nu mstr（pop＿option．v），γ，nu m2str（pop（i，1）），σ，nu m2str（pop（i，2））…，ε，nu m2str（pop（i，3）），s3］

Fitness（i）＝sv mtrain（train，apso）end

%寻优

f or i＝apso．option．max

f or j＝apso＿option．popsize%速度更新

V（j）＝apso＿option．w V＊V（j）＋apso＿option．c1＊rand＊（local＿y（j）－pop（j））＋pso＿option．c2＊rand＊（whole＿y－pop（j））；

if V（j，1）＞Vγmax

V（j，1）＝Vγmax；

end

if V（j，1）＜Vγmin

V（j，1）＝Vγmin；

end

if V（j，2）＞Vσmax

V（j，2）＝Vσmax；

end

if V（j，2）＜Vσmin

V（j，2）＝Vσmin；end

if V（j，3）＞Vεmax

V（j，3）＝Vεmax；

end

if V（j，3）＜Vεmin

V（j，3）＝Vεmin；

end

3 基于APSO－SVM算法的实例分析

在2014年4月5日至7月5日期间对某建筑物进行20次沉降监测 以其中的一个点收集沉降数据，建立建筑物沉降的APSO－SV M算法预测模型。以前15期数据作为训练样本，预测建筑物沉降数据。

本文实验在windows7上运行，以APSO及SV M算法为基础，以matlab7．1为开发工具，根据选取最佳参数开发建筑物沉降APSO－SV M预测模型。

参数设置见表1。

表1 参数设置

%预测过程

test＿x＝X2；%预测数据输入

test＿y＝Y2；%预测数据输出

test＿x M＝map min max（＇apply＇，test＿x，train＿x PS）；

test＿y M＝map min max（＇apply＇，test＿y，train＿y PS）；

test＿x M＝test＿x M＇；%矩阵转置

test＿y M＝test＿y M＇；

%将预测集数据输入训练好的SV M［7］，进行预测

［test＿predict M，test＿mse］＝sv mpredict（test＿y M，test＿x M，model）；

test＿predict＝map min max（＇reverse＇，test＿predict M＇，train＿y PS）；

利用函数Apsoprogress寻找到建筑物沉降训练数据的SV M模型最优参数best（γ，σ，ε），经过Tmax为100次的迭代，得到最优参数为：γ＝2．312 1，σ＝2．538 9，ε＝0．2，最 大 适 应 度 值 为－0．002。

现对建筑物沉降数据预测，并与传统的SV M算法预测的结果作比较，两种预测方法结果如表2与图2所示。

从表2可以看出，自适应粒子群优化的支持向量机算法最大相对误差为2．7%，高于传统的支持向量机算法的最大误差。从图2可以看出，传统的SV M算法在后期出现偏差较大的现象，而APSO－SV M算法经过部分参数的优化和选取 通过迭代次数的增加，提高预测精度，使其在预测中得到良好的效果。

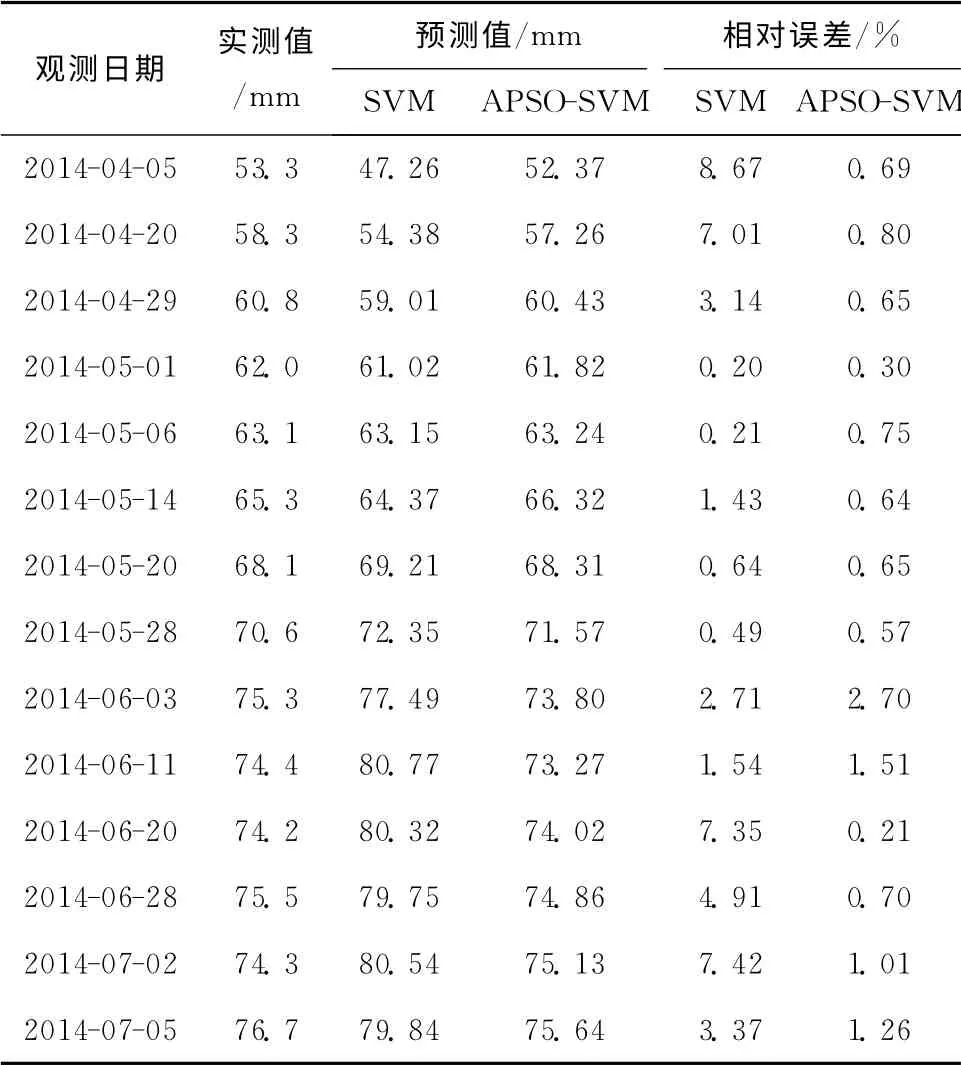
表2 沉降观测值、SVM预测值及APSO－SVM预测值对比

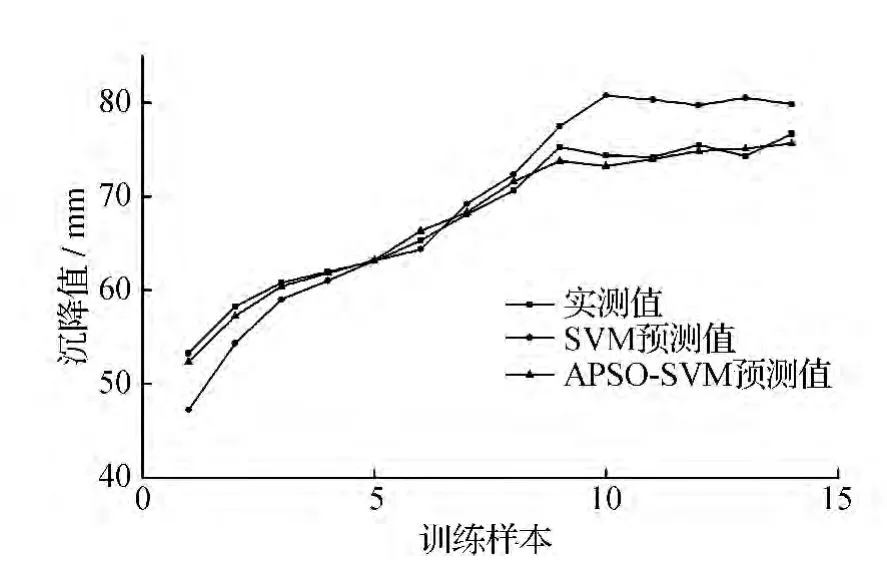
图2 沉降实测值、SVM预测值及APSO－SVM预测值

4 结 论

本文结合自适应粒子群优化算法，对支持向量机算法进行改进，提出自适应粒子群优化算法的支持向量机算法（APSO－SV M），利用APSO对SV M中的参数进行改进，结合建筑物变形特点建立APSO－SV M建筑物沉降预测模型。通过实例验证，取得良好的预测效果。实验数据表明：APSO－SV M算法经过参数的优化和选择，相比于传统的SV M算法，在预测精度上有较大的提高，在建筑物沉降预测方面有较高的推广价值。

［1］ 阎辉，张学工，李衍达．应用SV M方法进行沉积微相识别［J］．物探化探计算技术，2000，22（2）：158－164．

［2］ 陈贵敏，贾建援，韩 琪．粒子群优化算法的惯性权递减策略研究［J］．西安交通大学学报，2006，40（1）：53－56．

［3］ 俞欢军，张丽平，陈德钊，等．基于反馈策略的自适应粒子群优化算法［J］．浙江大学学报：工学版，2005，39（9）：1286－1291．

［4］ 金洋，郭茂祖，邓超．基于雁群启示的粒子群优化算法［J］．计算机科学，2006，33（11）：166－168，191．

［5］ MOHAN A L，KUMAR S M．Artificial neural networ k－based peak load forecasting using conjugate gradient methods［J］．IEEE Transactions on Power Systems，2002，17（3）：907－912．

［6］ JANSON S，MIDDENDORF M．A Hierarchical Particle Swar m Optimizer and Its Adaptive Variant［J］．IEEE Trans．on Systems，Man，and Cyber neticss，2005，35（6）：1272－1282．

［7］ 刘江华，程君实，陈佳品．支持向量机训练算法综述［J］．信息与控制，2002，31（1）：45－49．