六相永磁同步电机缺相容错控制

王永兴 温旭辉 赵 峰

(中国科学院电工研究所电力电子与电气驱动重点实验室 北京 100190)



六相永磁同步电机缺相容错控制

王永兴 温旭辉 赵 峰

(中国科学院电工研究所电力电子与电气驱动重点实验室 北京 100190)

为了实现六相永磁同步电机缺相后的矢量控制，根据定子磁势不变的原则，以铜耗最小为目标，对双Y移相30°六相永磁同步电机缺一相绕组的电流进行优化求解。根据所求得的优化电流，获得缺相后的变换矩阵，从而建立缺一相的六相永磁同步电机旋转坐标系下数学模型，并由此提出缺相后的解耦矢量控制方法。分析漏感和空间谐波对该容错控制下转矩脉动的影响，提出相应的抑制方法。实验验证了六相永磁同步电机容错控制算法的正确性，其有效减少了缺相后的转矩脉动，且具有较好的动态性能，提高了驱动系统的可靠性。

六相永磁同步电机 容错控制 优化电流 缺相 转矩脉动

0 引言

多相电机在电动汽车、舰船电力推进、风力发电及航空航天等要求大功率及高可靠性的应用场合得到越来越多的关注和认可。相数的增加使多相电机可提供比三相电机更多的控制自由度，增加的自由度可用来实现在缺相故障状态下的容错运行[1-6]。电机驱动系统中经常发生的电机绕组开路、功率器件开路和短路等故障都可通过硬件故障隔离的方法转变为电机缺相运行，通过容错控制使剩余的正常相可补偿故障引起的转矩脉动，从而简化了容错控制的复杂性。

现有多相驱动系统电机缺相的容错控制算法可分为两大类：第一类为优化电流控制。当多相电机驱动系统发生一相或几相故障时，通过调整剩余相的电流来保证磁势不变[7，8]。最初，学者们基于保证磁势不变的基础对未发生故障的相电流进行优化，优化的原则为保证相电流的幅值一致，同时保证铜耗最小[9-11]，或者只保证铜耗最小，而电流幅值不一致[12，13]，但这些方法都需要离线计算，而且其PWM调制方法大都采用滞环比较PWM。这一类方法未建立缺相后的电机数学模型，所以其电流控制只能采用滞环控制，不适合大功率高性能场合。第二类为磁场定向的矢量控制，该方法需要建立电机缺相后的解耦数学模型，从而实现磁场的定向。Y.Zhao等[14，15]通过解耦变换和非对称旋转变换建立了六相感应电机缺相下的多维解耦数学模型，从而实现了矢量控制，并给出了缺相下PWM的调制方法；文献[16]通过对称旋转变换推导缺相下五相永磁同步电机的数学模型，然后通过解耦变换矩阵使缺相后的电机电感矩阵对角化，从而实现了解耦的矢量控制；文献[17-19]给出了六相永磁同步电机缺相时的不对称旋转变换矩阵，但未给出具体的物理意义，通用性不强，而且此方法是一个近似的方法；文献[20]给出了双三相永磁电机不同中心点连接方式下的一相缺相模型，并给出了相应的控制方法。以上文献都是在一些理想的假设下得到的，未考虑漏感和空间谐波等因素的影响。

本文以中性点隔离的双Y移相30°六相永磁同步电机为研究对象，其绕组结构如图1所示。由于两套绕组的中性点隔离，所以此种电机最简单的容错控制方法为直接切除故障相所在的一套绕组，但这种方法会造成另一套绕组的电流增大1倍，同时未充分利用无故障相来输出转矩。本文对一相绕组断路情况进行研究，从理想假设出发，结合上述提到的两类方法，在最优电流计算的基础上建立电机缺相后的数学模型，实现缺相后基于最优电流的解耦矢量控制；同时分析了缺相后漏感和空间谐波对转矩脉动的影响，提出了相应的抑制方法，进一步减小转矩脉动，最后通过实验验证了本文所提出方法的正确性。

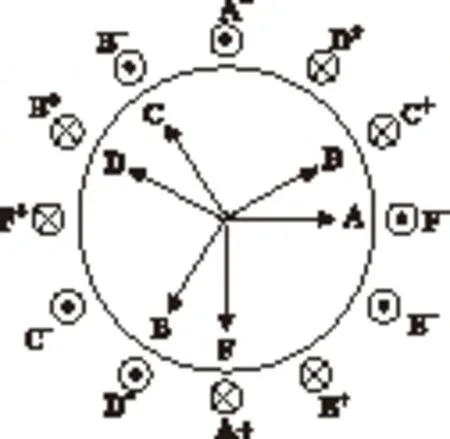
图1 双Y移相30°电机的绕组结构Fig.1 Winding structure of motor with double Y-connected phase-shift 30° windings

1 缺相的数学模型与控制

为了简化分析，首先对六相永磁同步电机做如下假设：

(1)磁路线性，忽略磁滞及涡流损耗；

(2)不计定子表面齿、槽的影响，转子上无阻尼绕组；

(3)绕组正弦分布；

(4)忽略电机漏感。

本节根据电机无扰运行的条件进行故障后的电机电流优化，并在此基础上对六相永磁同步电机一相绕组断路情况进行了建模，并给出了相应的控制方法。

1.1 缺相后的优化电流计算

以F相绕组断路为例来进行分析。缺相时，电机要实现无扰运行，需要电机在缺相前后定子磁势保持不变，其缺相后的定子磁势表达式为

f=NAiA+NBiB+NCiC+NDiD+NEiE

iDcos(γ-5α)+iEcos(γ-8α)]

(iA+δ-1iB+δ-4iC+δ-5iD+δ-8iE)ejγ]

(1)

式中，δ=ejπ/6；α=π/6；Ns为每相绕组匝数；γ为绕组空间角度；ix(x=A，B，C，D，E)为各相的电流；Nx(x=A，B，C，D，E)为各相的绕组函数，以B相为例，其绕组函数为NB=0.5Nscos(γ-α)。

假设缺相前定子磁势为

(2)

则式(1)和式(2)相等，有

iA+iBcos(α)+iCcos(4α)+iDcos(5α)+iEcos(8α)

=3Icosθ

iBsin(α)+iCsin(4α)+iDsin(5α)+iEsin(8α)=3Isinθ

(3)

式中，θ为电机电角度，θ=ωt，其中ω为电机的电角速度。

六相永磁同步电机采用两套绕组中性点隔离的结构，则各相电流满足

iA+iC+iE=0

iB+iD=0

(4)

式(3)和式(4)组成的线性方程组有5个变量，4个方程，其解不惟一，多的自由度可用于电机优化。这里选择的优化条件是定子铜损最小，铜损可表示为

(5)

这样电流求解的问题可等价为一个条件极值的求解问题，即：在满足式(3)和式(4)的条件下求式(5)的最小值。采用拉格朗日乘数法，最后可得F相缺相后其他相的电流为

(6)

令

式(6)所示的电流是电机缺相后以铜耗最小的原则优化获得的，其幅值和相位的变化是为了获得与故障前相同的旋转磁势，从而实现电机的无扰运行。

1.2 变换矩阵的确定

为了在建模和控制中实现铜耗最小，需要获得缺相后的变换矩阵和旋转矩阵。由于电机中性点隔离，根据式(4)的电流约束可得其零序分量为

(7)

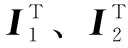
(8)

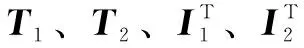
(9)

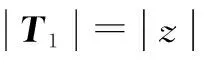
(10)

则其反变换矩阵为

(11)

另外，Park和反Park变换如式(12)所示

(12)

由此可得到五相静止坐标系与二相旋转坐标系的变换矩阵为

T5s/2r=C2s/2rT5s/2s

T2r/5s=T2s/5sC2r/2s

(13)

1.3 缺相后数学模型的建立

根据绕组函数理论，电机的电感可表示为

(14)

式中，r为定子内壁半径；l为电机定转子轴向长度；μ0为真空磁导率；Nx(γ)为绕组函数；σ(γ，θ)为气隙磁导函数，对于凸极式电机，可表达为

σ(γ,θ)=σ0+σ2cos 2(γ-θ)

(15)

式中，σ0、σ2分别为气隙磁导函数的直流和二次分量幅值。

通过式(14)可得到F相绕组断路后的自然坐标系下的电机电感为

(16)

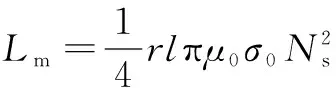
在自然坐标系下，电机电压方程可表示为

(17)

通过旋转变换可得

令udqz=T5s/2ru，idqz=T5s/2ri，则F相缺相的六相永磁同步电机在旋转坐标系下的数学模型为

(19)

式中，Ld=3Lm+3Lθ；Ld=3Lm+3Lθ；udqz=[uduquz]T；idqz=[idiqiz]T。

(20)

由式(19)可知，F相绕组断路后按磁势不变原则，所得到的旋转坐标系下的数学模型仍与电机的旋转角度θ相关，电感矩阵和磁链是时变的，所以此时不能像正常状态下的六相永磁同步电机那样对各电流分量进行解耦控制，传统的控制方法已无法应用到缺一相的六相永磁同步电机上。

1.4 缺相后的解耦容错控制

为了消除时变矩阵的影响，达到解耦控制的目的，对式(19)两边同时乘以A-1(θ)，则可得到

(21)

其中

(22)

令

(23)

则式(21)可写为

(24)

由电机的磁共能可知此时电机的转矩为

=3p((Ld-Lq)idiq+λPMiq)

(25)

式(24)的最后一项是与定子电阻相关的二倍频分量，其与转速无关，若忽略这一项的影响，则F相绕组断路后的六相永磁同步电机的数学模型与正常状态下的数学模型的形式是一致的、解耦的，所以系统可采用简单的PI控制器及前馈补偿(PI+FFController)来实现对转矩的稳定精确控制，前馈补偿项可根据式(24)

的最后一项来实现，控制框图如图2所示。由式(25)可看出此时转矩方程与正常状态下的方程一致，因此在绕组短路后转矩仍可实现解耦平滑地控制。

上面讨论了F相绕组断路时的容错控制，对于B、D两相可通过移动旋转坐标系的定向轴来实现，对于B相绕组断路时，将此时的B相当成F相，记为F′，同时将旋转坐标系的d轴由A相轴线逆时针旋转2π/3到C相轴线，此时的C相相当于原来的A相，定义为A′，其他各相依次旋转2π/3得到新的各相空间位置，如图3所示。

图2 F相绕组断路后的解耦控制框图Fig.2 Block diagram of decoupling control with F phase winding failure

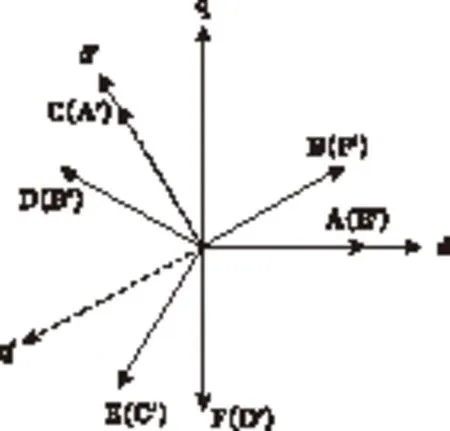
图3 B相绕组断路后的坐标定位Fig.3 Coordinate of B phase winding failure

此时

(26)

同理

(27)

相应的旋转角度为

(28)

通过式(26)～式(28)可得B相绕组断路时的控制框图如图4所示。

同理，类似可得D相绕组断路时的处理方法，但由于六相永磁同步电机是不对称分布的结构，无法直接通过F相断路的情况得到A、C、E相的数学模型和控制方法，只需在A、C、E相中任取一相断路的情况来得到相应的数学模型，从而获得其余两相断路的控制方法，分析方法与上述方法一致，在此不再赘述。

图4 B相绕组断路后的解耦控制框图Fig.4 Block diagram of decoupling control with B phase winding failure

2 转矩脉动评估

由于上述方法是在一些理想条件的假设中提出的，但实际中由于绕组端部必然存在漏磁的影响，电机漏感是存在的。而且在多相电机中，由于受到槽数的限制，电机绕组一般不可能设计成正弦绕组，甚至为了增加功率密度，可能会设计成整距绕组，此时空间谐波的存在对容错控制必然造成影响，从而产生转矩脉动。

下面以F相绕组断路的情况为例对这些影响进行分析。由于磁路线性，所以此处分别对漏感和空间谐波单独作用时的影响进行分析，将其叠加到1.3节的数学模型上，即为考虑了非理想因素的六相永磁同步电机的容错控制。

2.1 电机漏感的影响

在1.4节提出的容错控制方法中，忽略了电机漏感的影响，但在实际多相电机中漏感非常重要，其对谐波有很强的滤波作用，此处只考虑漏感的作用来评估其所产生的影响和造成的转矩脉动。

当只考虑漏感的作用，则缺相后的漏感电压方程可写为

(29)

式中，us_ls=[uA_lsuB_lsuC_lsuD_lsuE_ls]T；Lls为电机漏感。

式(29)通过式(10)、式(12)和式(23)变换到等效旋转变换坐标下为

(30)

从式(30)可知，微分项中存在二倍频的时变量，但由于其在微分项中，其在动态过程中对控制的影响较小，可忽略不计。第二项是与电机转速相关的二倍频时变量，随着转速的升高，这一项的作用会增强，其对电流的控制起到了二倍频交流扰动的作用，造成交、直轴电流的波动，进而造成转矩存在二倍频的波动，所以可通过提高电流环带宽来克服扰动的影响，如果要得到更高的性能，可将式(30)采用参数前馈补偿方法加入到如图2所示的控制框图中来消除其对电流控制的影响，减小电流波动，此时其产生的转矩为

(31)

从而可消除漏感对缺相后的控制系统的影响。

2.2 五次空间谐波的影响

由于缺相的影响，电机自由度降低，五次谐波已无法与基波保持正交[21]，这样其也会对电流控制和转矩脉动产生影响，为简化分析，忽略基波和五次谐波的耦合，只考虑五次空间谐波的作用。而且对于五次空间谐波，电机的凸极效应很小，可忽略，则只考虑五次空间谐波的作用所对应的缺相后的电压方程为

(32)式中，us_s5=[uA_s5uB_s5uC_s5uD_s5uE_s5]T；Λm5=λm5[cos5θcos5(θ-α) cos5(θ-4α) cos5(θ-5α) cos5(θ-8α)]T；λm5为五次谐波磁链。

(33)

式中，Lm5为五次谐波电感。只考虑五次空间谐波的等效电压方程为

(34)

由式(34)可看出，微分项中存在二倍频的时变量，但由于其在微分项中，其在动态过程中对控制的影响较小，可忽略不计。第二项和第三项是与电机转速相关的二倍频时变量，其对电流的控制起到交流扰动的作用，虽然可通过前馈补偿的方法来消除其对电流控制的影响，减小电流的波动，但其仍会产生相应的转矩脉动，这部分转矩脉动可表示为

15pλPM5izsin5θ

(35)

若电流能够无静差地跟踪，使iz=0，由式(35)可看出其转矩含有四倍频和六倍频的脉动，其大小与id、iq和λPM5有关，各频次的转矩脉动幅值可表示为

(36)

综上所述，电机的漏感和五次空间谐波均会对电机的缺相容错控制的电流控制造成影响，从而产生转矩脉动，但漏感对转矩脉动的影响可通过前馈补偿的方法加以消除，而五次空间谐波对转矩脉动的影响通过控制只能减小，而不能消除。

为了验证漏感和五次空间谐波对转矩脉动的影响，以表1中所示六相永磁同步电机参数进行仿真，以F相绕组在0.15 s发生断路为例，仿真结果如图5所示，在0.15～0.20 s之间容错控制中未加入漏感和空间谐波的前馈补偿算法，所以交、直轴电流的波动较大，0.20 s后加入前馈补偿算法，交、直轴电流波动减小到发生故障前水平，但转矩脉动幅值减小约50%，这与理论分析一致，另外图6给出了加入补偿算法前后的转矩谐波分析，从图中可看出，在未加入补偿算法前，转矩脉动存在二倍频、四倍频和六倍频

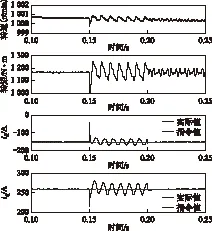
图5 加入补偿算法前后的转速、转矩和电流波形Fig.5 Speed，torque and current waves with and without compensation algorithm

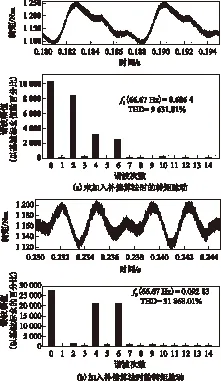
图6 转矩脉动FFT分析Fig.6 FFT analysis of torque ripple

转矩脉动，其主要是由于漏感及电流中的二次波动造成的，而加入补偿算法后，转矩中只存在四倍频和六倍频的转矩脉动且幅值基本相等，其主要是由于五次谐波的影响，如式(36)所示，与理论分析一致。

3 实验验证与结果分析

为了验证上述缺相故障的数学模型及容错控制方法的正确性，在一台双Y移相30°六相永磁同步电机上进行实验验证，电机参数见表1，实验台架如图7所示，采用将某一相绕组开路来模拟缺相故障；由于转矩传感器的采样速度不足以采集转矩脉动，所以此处采用转速信号的波动来体现转矩脉动；另外，由于基于载波的PWM(CPWM)是相调制方式[22]，其尤为适合在缺相后的不平衡相电压的调制，所以本文的容错控制采用CPWM调制方式来实现逆变器的电压调制，便于实现和工程应用。

图7 实验平台照片Fig.7 The picture of test bench

参数数值参数数值Rs/Ω0.005λm1/Wb0.13284Ld1/mH0.3864λm5/Wb-0.00263Lq1/mH1.0388J/(kg·m2)0.01Lls/mH0.08极对数p4Ls5/mH0.1231

以F相绕组断路来验证一相绕组断路容错控制算法，系统的外环控制采用转速控制，此时电机转速脉动可体现转矩脉动，设电机转速为300 r/min，在图8和图9中，当F相绕组发生断路时，首先不采用容错控制算法，从图8可知，此时转速脉动较大，即转矩脉动较大，电流含有大量谐波，而且从图9可看出此时的交、直轴电流存在约20 A的波动，电机有异响；然后控制算法切换到无补偿的容错控制算法，此时未考虑电机漏感及空间谐波等非理想因素的影响，转矩脉动减小约50%，交、直轴电流波动同样减小为10 A；最后将算法切换到带有前馈补偿的容错控制算法后，相电流的幅值和相位与理论分析基本一致，交、直轴电流进一步改善，已无明显波动，验证了本文对转矩脉动的分析及相应容错算法的正确性。

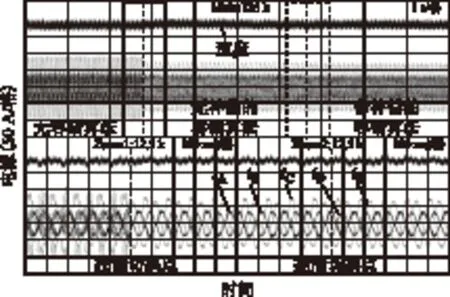
图8 F相绕组断路容错控制时的相电流和转速波形Fig.8 Phase currents and speed waves with fault-tolerant control for F phase winding failure

图9 F相绕组断路容错控制时的id、iq和相电流波形Fig.9 id、iq and phase current waveforms with fault-tolerantcontrol for F phase winding failure

为了验证容错算法的动态性能，设定系统工作在转矩环控制下，电机转速为300 r/min，图10为F相绕组断路时，转矩发生100%阶跃的电流响应波形，从图中可知，容错控制后的系统具有较好的动态性能，可达到未发生绕组断路故障的水平。

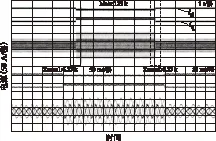
图10 F相容错控制下的转矩阶跃响应波形Fig.10 Current response waveforms of torque step with fault-tolerant control for F phase winding failure

图11显示了B相绕组发生断路故障时容错控制下的电流波形，此时的容错控制是在F相绕组断路的数学模型下获得，各相电流的幅值和相位与理论分析一致，验证了采用坐标轴旋转来获得任意相绕组断路容错控制方法的正确性。

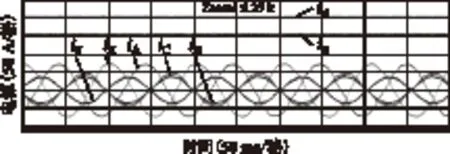
图11 B相容错控制下的电流波形Fig.11 Currents waves with fault-tolerant control for B phase winding failure

4 结论

本文以中性点隔离的双Y移相30°六相永磁同步电机为研究对象，对缺一相故障的容错控制进行了研究，得到以下结论：

1)以铜耗最小为目标，通过优化计算获得六相永磁同步电机缺一相故障的优化电流，保证故障前后的定子磁势不变。

2)以优化电流为基础，得到此时的变换矩阵，从而推导获得缺一相绕组的电机数学模型，从而提出相应的容错控制算法，实现故障后的解耦矢量控制，实验验证了容错控制方法的正确性。

3)在一相缺相的容错控制基础上，通过坐标变换可获得其他相缺相时的容错控制，并通过了实验验证。

4)分析了容错控制下漏感和五次空间谐波对转矩脉动的影响，通过补偿可抑制漏感产生的转矩脉动，但只能抑制五次空间谐波对电流的影响，无法完全消除其对转矩脉动的影响。

[1] Mendes A M S，Cardoso A J M.Fault-tolerant operating strategies applied to three-phase induction-motor drives[J].IEEE Transactions on Industrial Electronics，2006，53(6)：1807-1817.

[2] 刘自程，郑泽东，彭凌，等.船舶电力推进中十五相感应电机同轴运行及容错控制策略[J].电工技术学报，2014，29(3)：65-74. Liu Zicheng，Zheng Zedong，Peng Ling，et al.Fixed joint double fifteen-phase induction motor control and fault-tolerant control in ship propulsion system[J].Transaction of China Electrotechnical Society，2014，29(3)：65-74.

[3] Villani M，Tursini M，Fabri G，et al.High reliability permanent magnet brushless motor drive for aircraft application[J].IEEE Transactions on Industrial Electronics，2012，59(5)：2073-2081.

[4] Guohai L，Junqin Y，Wenxiang Z，et al.Design and analysis of a new fault-tolerant permanent-magnet vernier machine for electric vehicles[J].IEEE Transactions on Magnetics，2012，48(11)：4176-4179.

[5] Aroquiadassou G，Mpanda M A，Betin F，et al.Six-phase induction machine drive model for fault-tolerant operation[C].IEEE International Symposium on Diagnostics for Electric Machines，Power Electronics and Drives，Cargese，France，2009：1-6.

[6] Demba D，Mohamed E H B，Abdessalam M.A fault-tolerant control architecture for induction motor drives in automotive applications[J].IEEE Transactions on Vehicular Technology，2004，53(6)：1487-1495.

[7] Alcharea R，Nahidmobarakeh B，Baghli L，et al.Decoupling modeling and control of six-phase induction machines under open phase fault conditions[C].IECON 2006-32nd Annual Conference on IEEE Industrial Electronics，Paris，France，2006：5101-5106.

[8] Bianchi N，Bolognani S，Pré M D.Strategies for the fault-tolerant current control of a five-phase permanent magnet motor[J].IEEE Transactions on Industrial Application，2007，43(4)：960-970.

[9] Jen-Ren F，Lipo T A.Disturbance-free operation of a multiphase current regulated motor drive with an opened phase[J].IEEE Transactions on Industry Applications，1994，30(5)：1267-1274.

[10]Toliyat H A.Analysis and simulation of five-phase variable-speed induction motor drives under asymmetrical connections[J].IEEE Transactions on Power Electronics，1998，13(4)：748-756.

[11]Parsa L，Toliyat H A.Fault-tolerant interior permanent magnet machines for hybrid electric vehicle applications[J].IEEE Transactions on Vehicular Technology，2007，56(4)：1546-1552.

[12]Wang J，Atallah K，Howe D.Optimal torque control of fault tolerant permanent magnet brushless machines[J].IEEE Transactions on Magnetics，2003，39(5)：2962-2964.

[13]Sun Z G，Wang J B，Jewell G W，et al.Enhanced optimal torque control of fault-tolerant PM machine under flux-weakening operation[J].IEEE Transactions on Industrial Electronics，2010，57(1)：344-353.

[14]Zhao Y，Lipo T A.Modeling and control of a multi-phase induction machine with structural unbalance.Part I：Machine modeling and multi-dimensional current regulation[J].IEEE Transactions on Energy Conversion，1996，11(3)：570-577.

[15]Zhao Y，Lipo T A，Modeling and control of a multi-phase induction machine with structural unbalance.Part Ⅱ：Field-oriented control and experimental verification[J].IEEE Transactions on Energy Conversion，1996，11(3)：578-584.

[16]Hyung-Min R，Ji-Woong K，Seung-Ki S.Synchronous frame current control of multi-phase synchronous motor part ii-asymmetric fault condition due to open phases[C].Conference Record of the 2004 IEEE Industry Applications Conference，Seattle，Washington，USA，2004：268-275.

[17]周马山，欧阳红林，童调生，等.不对称多相PMSM的矢量控制[J].电工技术学报，2004，19(12)：37-41. Zhou Mashan，Ouyang Honglin，Tong Tiaosheng，et al.Vector control of multiphase PMSM with asymmetric structure[J].Transactions of China Electrotechnical Society，2004，19(12)：37-41.

[18]欧阳红林，周马山，童调生.多相永磁同步电动机不对称运行的矢量控制[J].中国电机工程学报，2004，24(7)：145-150. Ouyang Honglin，Zhou Mashan，Tong Tiaosheng.Vector control of nulti-phase permanent magnet synchronous motor with asymmetric structure[J].Proceedings of the CSEE，2004，24(7)：145-150.

[19]朱鹏，张晓峰，乔鸣忠，等.五相集中整距绕组感应电机缺相容错控制[J].中国电机工程学报，2011，31(33)：131-137. Zhu Peng，Zhang Xiaofeng，Qiao Mingzhong，et al.Tolerant control strategy for five-phase concentrated full-pitch windings induction motor under open phases fault[J].Proceedings of the CSEE，2011，31(33)：131-137.

[20]杨金波，李铁才，杨贵杰.一相开路双三相永磁同步电机建模与控制[J].电工技术学报，2011，26(10)：167-173. Yang Jinbo，Li Tiecai，Yang Guijie.Modeling and control of dual three-phase PMSM with one open phase[J].Transactions of China Electrotechnical Society，2011，26(10)：167-173.

[21]薛山，温旭辉，王又珑.多相永磁同步电机多维控制技术[J].电工技术学报，2008，23(9)：65-69. Xue Shan，Wen Xuhui，Wang Youlong.Multi-dimensional control in multiphase permanent motor drives[J].Transactions of China Electrotechnical Society，2008，23(9)：65-69.

[22]Cursino B J，Antonio M N L，Edison R C da S，et al.Digital scalar pulse-width modulation：a simple approach to introduce non-sinusoidal modulating waveforms[J].IEEE Transaction on Power Electronics，2001，16(3)：351-359.

The Fault-tolerant Control for Six-phase Permanent Magnet Synchronous Machines with One Phase Failure

WangYongxingWenXuhuiZhaoFeng

(Key Laboratory of Power Electronics and Electric Drive Institute of Electrical Engineering Chinese Academy of Sciences Beijing 100190 China)

In order to realize vector control of the six-phase permanent magnet synchronous machine (PMSM) with one phase failure，optimized currents of the six-phase PMSM containing double Y-connected phase-shift 30° windings with one phase failure are found based on the principle of the constant stator magnetic motive force concerning minimum copper loss.According to the optimized currents，the transformation matrix has been got to establish the mathematical model of the six-phase PMSM with one phase failure in the rotating coordinates.And thus the decoupling vector control method is proposed with one phase failure.Besides，the leakage inductance and the spatial harmonic which affect torque ripple in the fault-tolerant control are analyzed and the corresponding inhibitive method is provided.Experiments are carried out to verify the correctness of the fault-tolerant control for six-phase PMSM.The proposed fault-tolerant control method can reduce the torque ripple effectively and have a better dynamic performance，which ensures the reliability of the drive system.

Six-phase PMSM，fault-tolerant control，optimized currents，phase failure，torque ripple

国家自然科学基金重点项目(61034007)资助。

2014-11-09 改稿日期2014-12-30

TM315

王永兴 男，1985年生，博士研究生，研究方向为电机运行理论及控制。(通信作者)

温旭辉 女，1963年生，研究员，博士生导师，研究方向高功率密度电机驱动系统研究。