IGS跟踪站的大地高时间序列特征分析

徐克红，程鹏飞，文汉江

（1．辽宁城市建设职业技术学院 测绘系，辽宁 沈阳110122；2．国家测绘产品质量检验测试中心，北京100830；3．中国测绘科学研究院，北京100830）

IGS跟踪站自1994年成立以来，在全球建立很多GPS观测站，至今GPS跟踪站已经积累了10多年的GPS数据，使得GPS成为观测地壳运动的主要手段，成功应用于地壳水平运动的观测研究。而在高程方面，由于受到诸多因素的影响，变化较为复杂，使得其精度低于水平位移。但由于有多年的资料积累，高程方向的资料信息同样十分丰富，且精度有所提高。同时，台站坐标的精度对观测量的精度有直接的影响，所以对台站高程方向的时间序列进行分析有利于进一步提高观测量的精度。

本文选用我国北京房山、昆明、上海、拉萨等跟踪站，采用奇异谱分析的方法对以上台站大地高时间序列进行分析，研究该分析方法的可行性，以及高程方向的变化规律和周期特性，并与Fourier分析的结果进行比较。

1 奇异谱分析

主成分分析（Principal Co mponent Analysis，PCA），也称为经验正交函数（Empirical Ort hogonal Function，EOF），可以由多维的时间序列中获取时间序列的主要成分，是常用的多元统计分析方法之一，主要作用是将多个彼此相关的指标变换为少数几个彼此独立的综合指标即主成分，且这些主成分能反映原始数据的几乎全部信息，其中，常用于对一维的时间序列进行分析的方法称为奇异谱分析（Singular spectr u m anal ysis，SSA）。

奇异谱方法（SSA）是一种特别适合于研究周期振荡行为的分析方法，它是从时间序列的动力重构出发，并与经验正交函数相联系的一种统计技术，是EOF分解的特殊应用。分解的空间结构与时间尺度密切相关，可以较好地从含噪声的有限尺度时间序列中提取信息，目前已应用于多种时间序列的分析中。

SSA在数学形式上对单变量序列Xi1＜i＜N）展开为

式中：M为窗口长度或嵌入长度，依研究对象确定；Ek为原序列X1，…，XN的迟后自协方差矩阵Tx的归一化的特征向量，矩阵Tx具有Toeplitz结构，维数M×M；Tx的每个特征向量Ek的M个分量构成一个时间序列，反映X序列中的时间演变型，称Ek时间特征向量（简称T－EOF）；αk称时间主分量（简称T－PC），为原序列在第K个T－EOF上的正交投影

计算出Ek及αk后，可重建一个长度为N的序列，对应于第K个特征值的重建分量依下式计算：

原始序列Xi是所有重建分量之和

重建分量可用于提取感兴趣的信号，过渡掉噪声。由于重建分量是根据特征值方差贡献大小排列，一般不足前一半的重建分量已能很好地逼近原序列的变化过程。

SSA能很好地从时间序列中分离出周期介于（M／5，M），谱宽小于1／M 的振荡，并且可选择若干有意义的分量进行序列重建。其中低频信号的重建分量显示了原始序列的主要演变特征。

2 Fourier变换

在信号处理中，重要的方法之一是Fourier变换，它架起了时间域和频率域之间的桥梁，实现了从时域到频域的信号分析。Fourier变换一直统治着线性实不变信号处理，最主要的原因就是Fourier变换所用的正弦波eiωt是所有线性时不变算子的特征向量。

给定实的或复的离散时间序列x0x1xN－1，则 序 列 ｛xn｝的离散 Fourier变 换（Discrete Fourier Transf or m，DFT）为

从物理意义上讲，Fourier变换的实质是把波形分解成许多不同频率的正弦波的叠加，这样就可以从时域转换到频域实现对信号的分析。

虽然Fourier变换能够将信号的时域特征和频域特征联系起来，但只能从信号的时域和频域分别观察，不能将二者结合起来。这是因为信号时域波形中不包含任何频域信息，而其Fourier谱是信号的统计特性，它是信号整个时域内的积分，没有局部化信号分析的功能，所以不具备时域信息。

3 GPS台站大地高时间序列奇异谱分析

分别对北京、上海、昆明和拉萨4个台站的高程方向的日观测数据的时间序列进行了奇异谱分析。所用数据为：日采样的NEU数据中的U方向的数据，采样数据的时间段为：2000—2006年。

此外，为了减少时间序列中每日观测值跳变的影响，在计算中以7 d即一周为采样单位，对日观测数据进行处理后对该时间序列进行奇异谱分析，同时与对应的日观测数据的分析情况进行比较。

3．1 日采样数据分析

分别取M＝180和M＝360对各台站的时间序列进行奇异谱分析，并对前3阶分量进行重构，结果如图1～4所示（图中（a）是该站的日采样原始时间序列图）。其中，M分别取180和360时，各台站各阶模式所占比重如表1所示。

由图可见，分别对M取180和360的情况分析如下：

M＝180的情况：各站的第1模式均反映了各台站的长期信号，第2模式反映了台站的周年信号，其中，拉萨站反映最为明显，昆明站和北京房山站所反映信号相似。第3模式反映了台站的半周年信号，其中，昆明站反映最为明显，拉萨站在2000—2005年基本看不出该周期性。这与各台站所处的地域有关。

表1 各阶模式所占比重%

图1 昆明站大地高时间序列及前3阶EOF

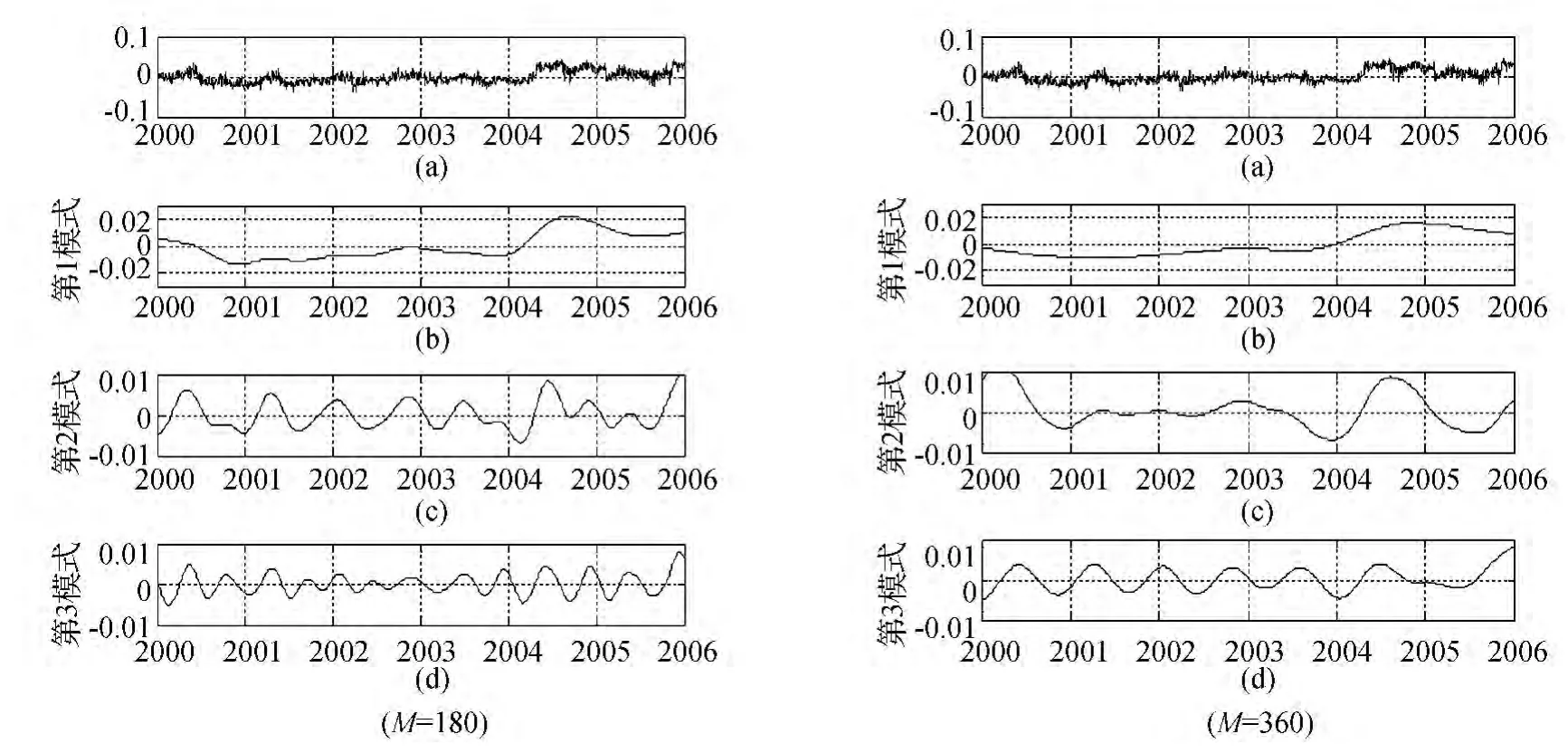
图2 北京房山站大地高时间序列及前3阶EOF

图3 上海站大地高时间序列及前3阶EOF

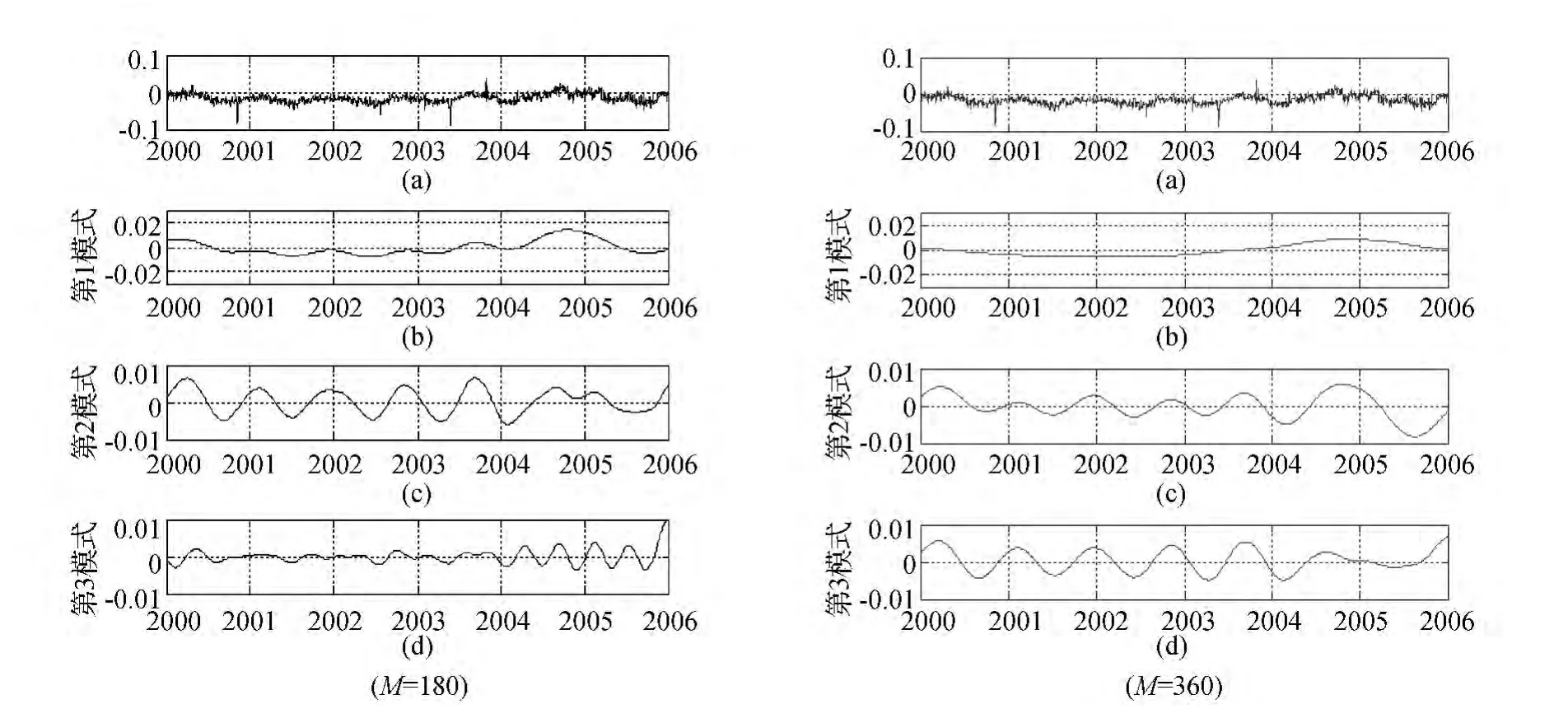
图4 拉萨站大地高时间序列及前3阶EOF

M＝360的情况：各站的第1模式均反映了各台站的长期信号，第2模式反映了台站的两周年信号，其中，上海站最明显。第3模式反映了台站的周年信号，其中，拉萨站反映最为明显。

M取180与取360的情况相比：M＝360的各阶模式都较M＝180的情况平滑，同时，两种情况均反映了台站的长期信号和周年信号。

3．2 周采样数据分析

同样对各台站的前3阶分量进行重构，如图5～8所示（每幅图中的（a）均为该台站的周采样时间序列图）。其中，各台站均取M＝50，各模式所占比重为：昆明：第1模式44．21%，第2模式18．56%，第3模式10．38%；北京房山：第1模式49．93%，第2模式16．60%，第 3 模 式 8．33%；上 海：第 1 模 式26．97%，第2模式22．36%，第3模式13．39%；拉萨：第1模式29．30%，第2模式22．23%，第3模式19．09%。

由图可见，长期信号反映明显，第2模式所反映的周期特性不明显，与日采样数据信号所反映的情况有差别。昆明、北京房山、拉萨的第3模式均反映了各台站周年的周期特性，而上海站的第3模式则反映了半年的周期特性，与其他3个台站有差别。

3．3 日采样和周采样的比较

对日采样和周采样时间序列分别进行了重构，并进行了傅立叶分析，如图9～12所示。

由图可见，昆明站和拉萨站的图中（c）、（d）均反映了一个明显的周期，图中（c）：333 d（昆明），323 d（拉萨）；图中（d）：350 d（昆明），318 d（拉萨）；北京房山站和上海站的图中（c）、（d）均反映了两个明显周期，（c）图：715 d，286 d（北京房山），602 d，250 d（上海）；（d）图：737 d，280 d（北京房山）；587 d，257 d（上海）。由此可见，该方法所得的各台站的周期与EOF分析所得的结论基本一致。

图5 昆明站周采样时间序列及前3阶EOF

图6 北京站周采样时间序列及前3阶EOF

图7 上海站周采样时间序列及前3阶EOF

图8 拉萨站周采样时间序列及前3阶EOF

图9 昆明站傅立叶变换

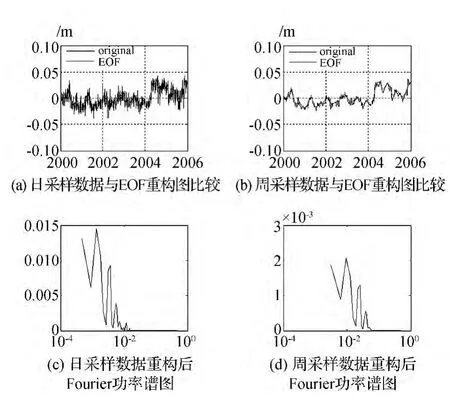
图10 北京房山站傅立叶变换

图11 上海站傅立叶变换

图12 拉萨站傅立叶变换

4 结 论

1）奇异谱分析和Fourier分析都很好地反映了各台站大地高方向时间序列的主要趋势和周期特性，且奇异谱分析方法所显现的周期特性比较直接。

2）由奇异谱分析结果可知：各台站均具有明显的周年和半周年的周期特性，同时可知，各台站变化规律具有一定的地域性有待进一步研究。

3）日采样数据信号和周采样数据信号均较好地反映了台站的长周期特性和周年特性，而在半周年信号的反映上，日采样数据信号比周采样数据信号表现明显。同时，二者比较可见，由于周采样是对日采样进行了一次平滑，所以反映信号也比较平滑，所显现的周期特性也比较明确。

［1］ 朱文耀，符养，李彦．GPS高程导出的全球高程振荡运动及季节变化［J］．中国科学，2003，35（5）：470－481．

［2］ 杨强，党亚民，秘金钟．基于IGS连续跟踪站的GPS高程时间序列分析［J］．测绘科学，2007，32（3）：55－57．

［3］ 张鹏，蒋志浩，秘金钟，等．我国GPS跟踪站数据处理与时间序列特征分析［J］．武汉大学学报：信息科学版，2007，32（3）：251－254．

［4］ 刘小明，任雅奇，姚飞娟．高精度GPS数据处理中IGS站的选取［J］．测绘科学，2014，39（6）：22－24．

［5］ 徐克红，程鹏飞，文汉江．太阳黑子数时间序列的奇异谱分析和小波分析［J］．测绘科学，2007，32（6）：35－38．

［6］ 文汉江，章传银．由ERS－2和TOPEX卫星测高数据推算的海面高异常的主成分分析［J］．武汉大学学报：信息科学版，2006，31（3）：221－223．

［7］ 钟秋珍，刘四清，何卷雄，等．奇异谱分析在太阳10．7 c m射电流量中期预测中的应用［J］．空间科学学报，2005，25（3）：199－203．

［8］ 余锦华，丁裕国，江志红．我国近百年气温变化的奇异谱分析［J］．南京气象学院学报，2000，23（4）：586－593．

［9］ 飞思科技产品研发中心．小波分析理论与 MATLAB7实现［M］．北京：电子工业出版社，2005．

［10］朱广彬，丁剑．NINO3海面温度异常时间序列的小波分析［J］．测绘科学，2006，31（3）：33－36．

［11］徐克红，王赫，王永富．基于SLR的GRACE卫星定轨中重力场模型对轨道精度的影响［J］．测绘工程，2011，20（3）：15－20．