压缩性修正对γ-Reθ转捩模型的影响研究

夏陈超，姜婷婷，郭中州，陈伟芳

(浙江大学航空航天学院，浙江杭州 310027)

压缩性修正对γ-Reθ转捩模型的影响研究

夏陈超，姜婷婷，郭中州，陈伟芳*

(浙江大学航空航天学院，浙江杭州 310027)

将基于流场当地变量的γ-Reθ转捩模型加入可压缩RANS方程计算程序，对平均流场控制方程、湍流和转捩控制方程进行基于LU-SGS的隐式紧耦合求解。结合三种压缩性修正方法对高超声速平板、双楔和圆锥流动进行了数值模拟，给出了壁面斯坦顿数、热流值和实验值的比较，以及湍动能和间歇因子分布云图。数值计算结果表明，相同来流湍流度下不同压缩性修正方法得到的转捩位置差别较大。相比于未修正的模型，基于当地马赫数压缩性修正后的转捩位置最靠后，其对带有分离的双楔流动预测较为准确;基于来流马赫数的压缩性修正仅使得转捩位置稍有延迟;对湍动能源项的压缩性修正可提高模型在转捩后湍流段的热流预测精度。

高超声速;RANS方程;γ-Reθ转捩模型;紧耦合;压缩性修正

0 引言

边界层转捩是目前流体力学领域的研究热点和难点，也是航空航天工程中的关键问题。虽然国内外研究者已经做了大量卓有成效的工作，但对转捩相关机理的认识和理论分析仍有待提升。对高超声速飞行器而言，流动形态的变化关系到飞行器的升阻特性、热防护以及发动机中的流动品质等。准确预测转捩位置、转捩区长度以及气动力/热环境对飞行器设计有重要意义。

相比于直接数值模拟(DNS)和大涡模拟(LES)，基于RANS的数值模拟是当前工程上预测湍流和转捩较为经济和高效的方法，其中Huang［1］、Walters［2］和Lantry［3］等的研究具有代表性。Lantry等提出的基于经验关系式的γ-Reθ转捩模型在k-ω SST两方程湍流模型的基础上添加了两个输运方程，一个是间歇因子γ的输运方程，一个是动量厚度雷诺数Reθ的输运方程。γ-Reθ模型是基于流场当地变量的转捩模型，可以和现代CFD程序相兼容，相比于目前常用的eN方法［4］，具有更强的适用性。针对低速平板、翼型/机翼和涡轮机械的众多研究［5-7］表明γ-Reθ模型对自然转捩和分离转捩具有较好的预测能力。

一方面，虽然原始的γ-Reθ模型基于不可压实验发展而来，但 Krause［8］、You［9］、孔维萱［10］以及郑赟［11］等采用γ-Reθ模型对高超声速双楔和尖锥等流动的数值计算表明该模型也能较准确地预测高超声速流动中的转捩问题。另一方面，为增强该模型对高速流动问题的适用性，有必要进行适当的压缩性修正。Kaynak［12］给出了一种基于来流马赫数的压缩性修正关系式，对超声速平板的边界层转捩进行了预测;张晓东［13］则对经验关系式进行了基于当地马赫数的修正，通过对双楔模型的数值计算，得到的壁面压力系数与实验值吻合较好。总体而言，该模型目前主要应用于低速流动问题，其在高速流动情况下的压缩性修正研究还很少。本文将γ-Reθ模型编入课题组发展的基于SST湍流模型的可压缩RANS方程耦合求解程序，结合高超声速平板和圆锥等典型流动问题，通过数值模拟和对比，初步探索了三种压缩性修正方法对γ-Reθ模型预测转捩的影响，为该模型的进一步改进提供参考。

1 转捩模型

1.1 γ-Reθ转捩模型

γ-Reθ转捩模型包含间歇因子和转捩动量厚度雷诺数两个输运方程，其中间歇因子的输运方程为:

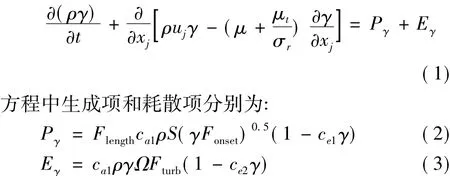
其中，Flength为转捩区长度控制函数，Fonset为转捩发生函数，Fturb用于抑制再层流化，相关参数详见文献［3］。

1.2 压缩性修正

由于原始的γ-Reθ模型中转捩动量厚度雷诺数Reθt关系式是通过不可压平板实验获得，因此将该模型应用于高速可压缩流问题时有必要进行适当的可压缩性修正(Compressibility Correction，文中用CC表示)。本文实现并对比了三种压缩性修正方法。

(1)CC=1

张晓东［13］基于高超声速风洞实验数据，给出了一种基于当地马赫数的压缩性修正关系式:

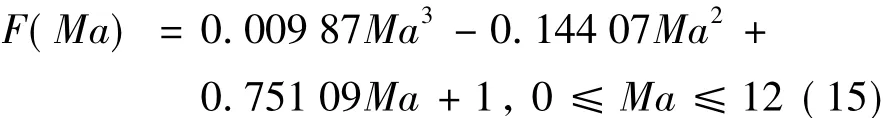
(2)CC=2

Kaynak［12］给出了一种基于来流马赫数的修正关系式:

虽然文献［12］给出了该关系式的适用范围(来流马赫数小于2.4)，本文仍将其视为一种潜在的修正方法，评估其压缩性修正效果。

(3)CC=3

Papp等人［14］在对其发展的基于SSGZ k-ε模型的工程转捩模型进行压缩性修正时在湍动能方程中添加了一个源项，形式如下:

本文参考该方法，将上述源项加入SST湍流模型的湍动能方程中进行修正。其中，，湍流马赫数，M't为考虑转捩效应的转捩湍流马赫数，系数λ的作用是当转捩湍流马赫数小于λ时不起作用，取值0.2，α1=2.5，α2=2.0，ε=βωk。

压缩性修正1和2的实施是将F(Ma)乘到转捩动量厚度雷诺数，压缩性修正3则是将Pe直接加到湍动能k方程的源项中。

2 数值方法

将 γ-Reθ转捩模型加入课题组发展的可压缩RANS程序，流动控制方程为雷诺平均的三维NS方程、SST两方程湍流模型方程以及γ-Reθ转捩输运方程。计算程序基于结构网格的有限体积方法，其中无黏通量采用计算效率和分辨率均较高的AUSMPW+格式［15］并采用MUSCL进行高阶插值，黏性通量采用中心差分进行离散。

为提高计算效率，时间推进采用Yoon和Jameson［16］提出的LU-SGS隐式方法，同时采用当地时间步长加速收敛。为克服源项刚性，对湍流和转捩输运方程中的负值耗散项进行隐式处理以增强矩阵对角占优［12］:

3 计算结果与分析

3.1 平板流动

高超声速平板流动算例取自Mee［17］的激波风洞实验结果。平板长1.5m，来流马赫数6.2，来流静温690K，来流静压5.4kPa，单位雷诺数为2.6×106。计算网格为224×150(流向和法向)，在壁面和前缘进行了加密，壁面第一层网格y+小于1(约0.5)。

图1和图2为两种来流湍流度情况下的平板壁面斯坦顿数分布，斯坦顿数定义为:

其中，qw为热流，ρ∞和u∞分别为来流密度和速度，h0∞为来流总焓，hw壁面焓。图中对比了无压缩性修正的γ-Reθ模型、三种压缩性修正的γ-Reθ模型、完全层流状态和完全湍流状态(SST模型)的结果。可以看出，层流和湍流的斯坦顿数与实验值吻合较好，转捩模型实现了层流到湍流的过渡，随着来流湍流度的增大，转捩位置前移，但相比于实验值，转捩区长度过长。相同湍流度条件下不同压缩性修正方法的转捩起始位置差异较大，方法1转捩位置最靠后，方法2居中，相比于无压缩性模型均延迟了转捩位置，方法3由于没有改变转捩模型经验关系式，其转捩位置与无压缩性模型基本一致，但其在一定程度上降低了湍流段的热流。

图3和图4分别为湍流度3%时无压缩性修正和采用压缩性方法2的流场湍动能云图，湍动能的急剧增大意味着转捩的发生，可以看出，进行压缩性修正后转捩位置有了明显的后移，即该压缩性修正方法限制了湍动能的发展。数值计算也表明，无压缩性修正时最大湍动能为61 611m2/s2，压缩性修正方法2得到的最大湍动能减少到了60 257 m2/s2。

图1 湍流度2%的平板壁面斯坦顿数Fig.1 Stanton number on flat plate(Tu=2%)

图2 湍流度3%的平板壁面斯坦顿数Fig.2 Stanton number on flat plate(Tu=3%)

图3 无压缩性修正的平板湍动能云图Fig.3 Contour of turbulence kinetic energy without compressibility correction

图4 压缩性方法2的平板湍动能云图Fig.4 Contour of turbulence kinetic energy with compressibility correction method 2

3.2 双楔流动

双楔几何外形［18］如图5所示，其第一个和第二个坡的角度分别为 9°和 20.5°，前缘钝化半径0.5mm。计算马赫数为8.1，来流单位雷诺数为3.8 ×106，来流静压520Pa，来流静温106K，壁面温度为300K，来流湍流度0.9%。钝头双楔计算网格如图6所示，网格在壁面、头部和拐角附近进行了加密，并保证第一层y+值小于1(约为0.3)。

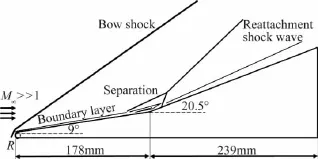
图5 双楔流动示意图Fig.5 Schematic of blunted double wedge flow

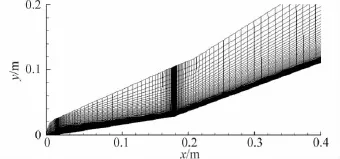
图6 双楔模型计算网格Fig.6 Grid of blunted double wedge

图7 双楔模型壁面压力分布Fig.7 Comparison of pressure coefficient of double wedge with blunt leading edge

图7 和图8分别为双楔模型壁面压力系数和斯坦顿数分布。可以看出，完全层流状态在拐角的分离区过大，斯坦顿数过低，完全湍流状态则未发生分离，斯坦顿数过高。转捩模型的结果与实验值更接近，其中，压缩性修正方法1的分离区大小、压力和斯坦顿数与实验值最为吻合，压缩性修正方法3与未修正的转捩模型相比，拐角后的湍流段壁面斯坦顿数较低。

图8 双楔模型壁面斯坦顿数分布Fig.8 Comparison of Stanton number of double wedge with blunt leading edge

图9 至图11给出了不同压缩性方法在拐角处的局部放大流线图和间歇因子云图，可以看出，间歇因子分布和流动的分离是相对应的，分离起始点之前的间歇因子保持很小的值，表明流动还是层流;分离之后，间歇因子迅速增长。从压缩性修正方法1到3，分离区逐渐减小，压缩性减弱，这与壁面压力和热流的分布趋势是一致的。

图9 压缩性方法1拐角处流线和间歇因子Fig.9 Streamline and intermittency factor around corner with compressibility correction method 1

图10 压缩性方法2拐角处流线和间歇因子Fig.10 Streamline and intermittency factor around corner with compressibility correction method 2

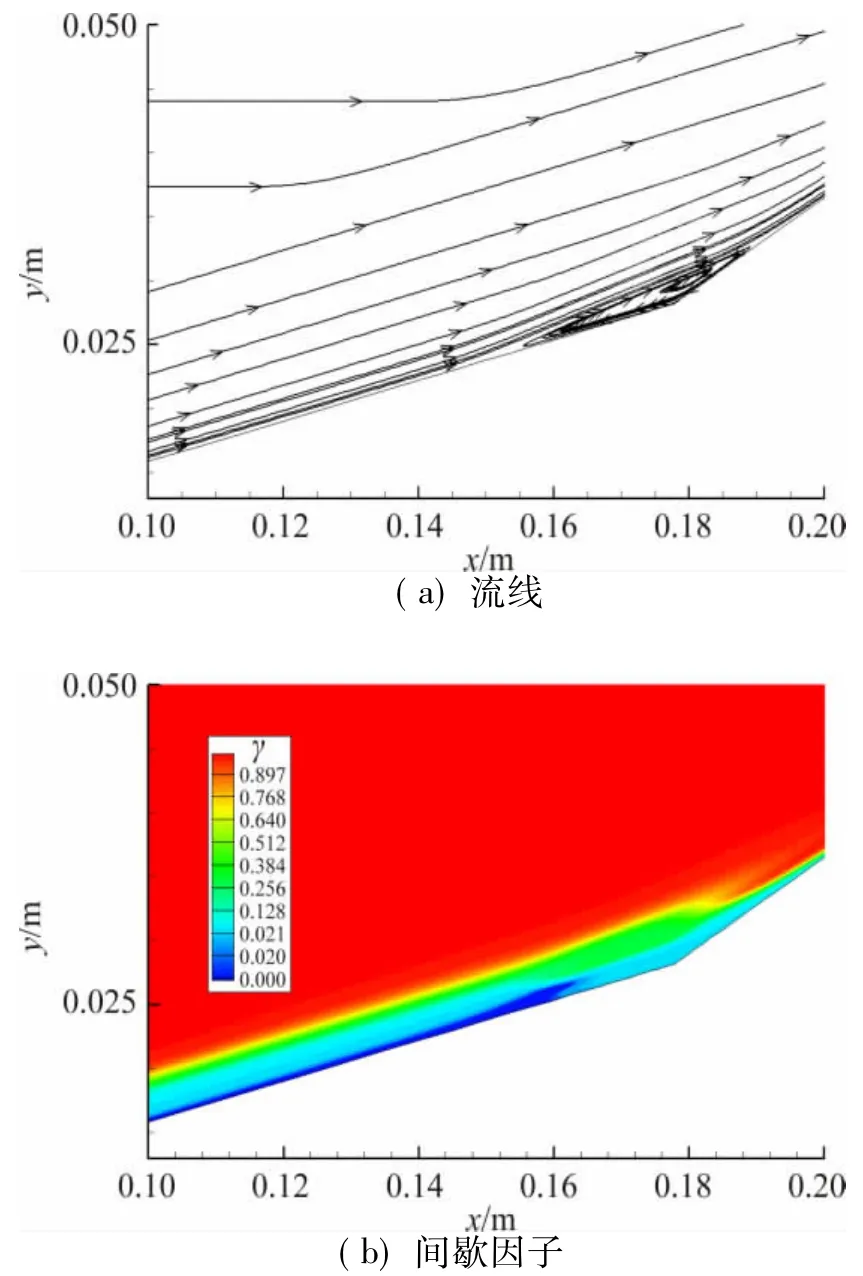
图11 压缩性方法3拐角处流线和间歇因子Fig.11 Streamline and intermittency factor around corner with compressibility correction method 3

3.3 圆锥流动

针对高超声速圆锥流动［19］进行数值计算，圆锥锥角为7°，头部钝化半径5 mm，如图12所示。来流马赫数7.15，来流静温214 K，壁温300 K，来流静压7 722 Pa，单位雷诺数为9.64×106。采用半模计算，网格量为106×78×29(流向、法向和周向)，壁面第一层网格间距为1×10-6m。

图12 圆锥几何外形Fig.12 Geometry of cone

由于不易实现计算与实验条件的完全一致，本文计算了多个来流湍流度的情况，图13至图15分别为来流湍流度0.2%、0.35%和0.5%条件下的圆锥表面热流分布对比。可以看出，完全层流的计算结果在层流段与实验值吻合，完全湍流的计算结果在湍流段热流比实验值偏高，转捩模型的结果与实验值更为接近，且随着来流湍流度的提高，转捩位置前移。相同湍流度条件下三种压缩性修正方法的转捩位置相差较大，方法1转捩位置最靠后(来流湍流度为0.2%时未发生转捩)，方法2居中，方法3转捩位置与无压缩性修正基本相同，趋势与3.1中的平板一致。压缩性修正方法3在转捩后的湍流段热量值较低，与实验值更接近。

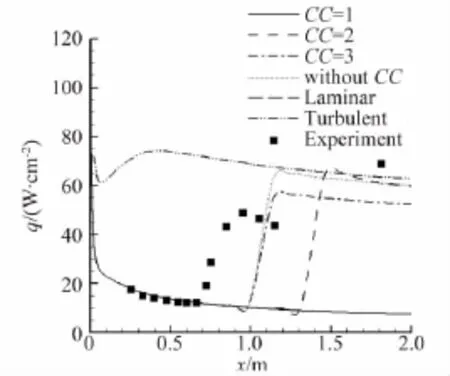
图13 来流湍流度0.2%壁面热流分布Fig.13 Heat flux on wall(Tu=0.2%)

图14 来流湍流度0.35%壁面热流分布Fig.14 Heat flux on wall(Tu=0.35%)

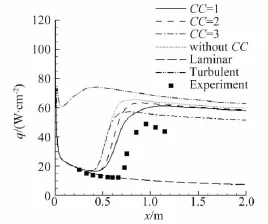
图15 来流湍流度0.5%壁面热流分布Fig.15 Heat flux on wall(Tu=0.5%)

4 结论

基于可压缩RANS方程计算程序，引入γ-Reθ转捩模型，采用三种压缩性修正方法对高超声速平板、双楔和圆锥进行了数值模拟并与实验结果进行了比较。研究表明，三种压缩性修正后的转捩模型在相同湍流度条件下的转捩位置相差较大。基于当地马赫数的压缩性修正有效地预测了带有分离的双楔流动，同时，相比于未修正的转捩模型，该修正会较大程度地延迟转捩位置。基于来流马赫数的压缩性修正仅使得转捩位置稍有延迟。湍动能方程源项的压缩性修正能降低转捩后湍流段壁面热流，使结果与实验值更加接近，对转捩位置没有影响。此外还可看出，对于不同的流动特性，相同的压缩性修正方式效果是不一样的，即很难得到对任何流动情况都适用的模型，实际情况中，应根据不同的流动特性进行湍流和转捩模型的选择。

总体而言，要将γ-Reθ转捩模型应用于高速流动问题还有许多值得改进的工作。相比于壁面压力系数，高超声速条件下壁面热流值预测精度的提高仍是一个挑战。本文中研究的压缩性修正方法均较为简单，将当地马赫数和湍动能源项修正相结合可能是一个更好的尝试。考虑更多转捩影响因素、适用范围更广的压缩性修正方法是今后的一个探索方向。

参考文献:

［1］Suzen Y B，Huang P G.An intermittency transport equation for modeling flow transition［R］.AIAA 2000-0287.2000

［2］Walters D K，Leylek J H.A new model for boundary-layer transition using a single-point RANS approach［J］.Journal of Turbomachinery，2002，126(1):193-202.

［3］Langtry R B，Menter F R.Transition modeling for general CFD applications in aeronautics［C］.Reno:43rd AIAA Aerospace Sciences Meeting and Exhibit，2005.

［4］Malik M，Balakumar P.Instability and transition in three-dimensional supersonic boundary layers［R］.AIAA-92-5049.1992

［5］Malan P，Suluksna K，Juntasaro E.Calibrating the γ-Reθtransition model for commercial CFD［R］.AIAA 2009-1142.2009

［6］Langtry R B，Menter F R.Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes［J］.AIAA Journal，2009，47(12):2894-2906.

［7］Wang Gang，Liu Yi，Wang Guangqiu，et al.Transitional flow simulation based on γ-Reθttransition model［J］.Acta Aeronautica et Astronautica Sinica，2014，35(1):70-79.(in Chinese)王刚，刘毅，王光秋，等.采用γ-Reθt模型的转捩流动计算分析［J］.航空学报.2014，35(1):70-79.

［8］Krause M，Behr M，Ballmann J.Modeling of transition effects in hypersonic intake flows using a correlation-based intermittency model［C］.Dayton:15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference，2008.

［9］You Y，Luedeke H，Eggers T，Hannemann K.Application of the γ-Reθttransition model in high speed flows［C］.Tours:18th AIAA/3AF International Space Planes and Hypersonic Systems and Technologies Conference，2012.

［10］Kong Weixuan，Yan Chao，Zhao Rui.γ-Reθmodel research for high-speed boundary layer transition［J］.Acta Aerodynamica Sinica，2013，31(1):120-126.(in Chinese)孔维萱，阎超，赵瑞.γ-Reθ模式应用于高速边界层转捩的研究［J］.空气动力学学报.2013，31(1):120-126.

［11］Zheng Yun，Li Hongyang，Liu Daxiang.Application and analysis of γ-Reθtransition model in hypersonic flow［J］.Journal of Propulsion Technology，2014，35(3):296-304.(in Chinese)郑赟，李虹杨，刘大响.γ-Reθ转捩模型在高超声速下的应用及分析［J］.推进技术，2014，35(3):296-304.

［12］Kaynak U.Supersonic boundary-layer transition prediction under the effect of compressibility using a correlation-based model［J］.Proceedings of the Institution of Mechanical Engineers，Part G:Journal of Aerospace Engineering，2012，226(7):722-739.

［13］Zhang X D，Gao Z H.Numerical discuss to complete empirical correlation in Langtry＇s transition model［J］.Applied Mathematics and Mechanics，2010，31(5):544-552.(in Chinese)张晓东，高正红.关于补充Langtry的转捩模型经验修正式的数值探讨［J］.应用数学和力学.2010，31(5):544-552.

［14］Papp J L，Kenzakowski D C，Dash S M.Extensions of a rapid engineering approach to modeling hypersonic laminar to turbulent transitional flows［R］.AIAA 2005-0892.

［15］Kim K H，Kim C，Rho O.Methods for the accurate computations of hypersonic flows:I.AUSMPW+scheme［J］.Journal of Computational Physics，2001，174(1):38-80.

［16］Yoon S，Jameson A.Lower-upper symmetric-Gauss-Seidel method for the Euler and Navier-Stokes equations［J］.AIAA Journal，1988，26(9):1025-1026.

［17］Mee D J.Boundary-layer transition measurements in hypervelocity flows in a shock tunnel［J］.AIAA Journal，2002，40(8):1542-1548.

［18］Neuenhahn T，Olivier H.Influence of the wall temperature and the entropy layer effects on double wedge shock boundary layer interactions［R］.AIAA 2006-8136.

［19］Maclean M，Mundy E，Wadhams T，Holden M，Johnson H，Candler G.Comparisons of transition prediction using PSE-chem to measurements for a shock tunnel environment［R］.AIAA 2007-4490.

Effects of compressibility correction on γ-Reθtransition model

Xia Chenchao，Jiang Tingting，Guo Zhongzhou，Chen Weifang*
(School of Aeronautics and Astronautics，Zhejiang University，Hangzhou 310027，China)

Boundary layer transition plays a significant role in the prediction of aerodynamic and aerothermodynamics characteristics of hypersonic vehicle.The commonly used correlation based on γ-Reθtransition model is implemented into a Reynolds-Averaged Navier-Stokes solver in order to evaluate its capability in hypersonic flows.The mean flow and turbulent flow equations are solved simultaneously based on the LU-SGS method.Three compressibility correction methods are adopted to simulate the hypersonic flows around a flat plate，a double wedge and a cone body.Results of Stanton number，heat flux on walls，contours of turbulence kinetic energy and intermittency factor are presented.The results of γ-Reθtransition model show better flow essential than that of full laminar or full turbulent results.The transition onset positions obtained by different compressibility methods under the same free stream turbulence intensity varied significantly.Compressibility correction based on local Mach number delays the transition onset greatly，while the correction of source term of turbulent kinetic energy equation improves the accuracy of heat flux on turbulent section of the wall.Rational selection of compressibility correction method should rely on the type of flow.Elaborate and reliable compressibility correction method still need to be further investigated.

hypersonic;RANS equations;γ-Reθtransition model;coupled method;compressibility correction

V211.3

:Adoi:10.7638/kqdlxxb-2014.0068

0258-1825(2015)05-0603-07

2014-07-14;

:2014-10-10

国家重点基础研究发展计划(2014CB340201)

夏陈超(1989-)，男，福建宁德人，博士生，流体力学专业.E-mail:aeroxia@zju.edu.cn

陈伟芳*(1970-)，男，博士，教授，研究方向为高超声速空气动力学.E-mail:chenwfnudt@163.com

夏陈超，姜婷婷，郭中州，等.压缩性修正对γ-Reθ转捩模型的影响研究［J］.空气动力学学报，2015，33(5):603-609.

10.7638/kqdlxxb-2014.0068 Xia C C，Jiang T T，Guo Z Z，et al.Effects of compressibility correction on γ-Reθtransition model［J］.Acta Aerodynamica Sinica，2015，33(5):603-609.