陷窝诱导涡结构数值模拟分析
刘 静,李 杰,蒋胜矩
(1.西北工业大学 翼型叶栅空气动力学国防科技重点实验室,陕西 西安 710072;2.中国兵器工业第203研究所,陕西 西安 710065)
0 引 言
旋涡是流动的肌腱,对于流场中旋涡的准确认识是发展科学的旋涡控制和应用技术的前提。陷窝作为一种涡流发生器,通过诱导产生涡结构注入边界层层动量,在流动分离控制、减阻及增强对流换热等很多方面都有应用研究[1-9]。陷窝具有在不带来明显的压力损失的前提下,引起流场持续的扰动的优良特点,这得益于陷窝所诱导涡结构奇特的流场扰动方式。
国内外用数值模拟和实验的手段进行陷窝的有关研究。目前的数值研究方向分为两类,第一类是以研究陷窝诱导涡结构非定常脱落的基于URANS和LES的研究;第二类是基于RANS的稳态假设下陷窝诱导涡结构及其应用的研究。URANS和LES方法着重研究陷窝诱导涡的非定常脱落性质。RANS则侧重于得到稳态假设下的涡结构、传热性能和流动控制等的时均特征。Isaev[1-3]等人开展基于 RANS的陷窝强化传热定常数值模拟研究,通过表面极限流线发现,深宽比0.2陷窝内的涡结构为双单元类龙卷风涡结构,类龙卷风涡从物面螺旋点升起,能引起流场的持续扰动,强化换热。Isaev[4]用 URANS和LES方法进行了陷窝诱导涡结构的非定常脱落频率的研究。谢永慧[5]用LES研究陷窝控制边界层分离研究中发现深宽比0.09陷窝内诱导的涡结构为马蹄涡,马蹄涡腿源自于物面焦点,马蹄涡头位于下游,马蹄涡周期性脱落,并在陷窝后形成发夹涡排。刘高文[7-8]用实验测量了深宽比0.2陷窝内的涡结构,发现会在陷窝背风面附近形成一个低速回流区,并发现气流经过陷窝后诱导形成一对尺寸较大的旋涡附着于尾迹区。何雅玲[9]用RANS研究陷窝强化换热,发现陷窝的介入使得流动中产生了旋涡死区,死区中的流体不容易从其中流出,降低了换热效果。
现有研究主要通过物面极限流线和空间流线来研究陷窝内涡结构,也没有对涡核处压力和轴向速度的细节分析的文献,为了澄清陷窝诱导涡结构及其对尾流的扰动方式,本文对布置单个陷窝两平板间充分发展段流动进行RANS数值模拟。首次利用张涵信的旋涡沿轴线的非线性分叉理论[10-11]和沿涡轴的轴向速度和压力分布等细致分析在稳态假设下陷窝内涡结构发展、演变及破裂的规律。研究显示本文模拟的陷窝内涡结构为失稳破裂的半涡环,破裂后涡量扩散形成弱纵向涡,形成对尾流的扰动。陷窝内的涡结构决定了陷窝后流场的扰动方式和强度。本文研究对陷窝的后续研究有指导意义。
1 物理模型的建立
物理模型为底板布置深宽比0.2陷窝的相距0.2m两平板之间充分发展段流动。计算区域取底板到两平板等分面之间,等分面设为对称面。计算模型如图1所示,矩形计算区域长0.406 4m,宽0.254m,高0.1m。流向为x向,展向为y向,高为z向。单个陷窝布置在底板上,陷窝中心和底板中心重合。陷窝表面直径为0.025 4m,陷窝深度为0.005 08m。陷窝深宽比为0.2,陷窝深度和两平板间距离之比为0.025。陷窝深度的设计依据过增元的场协同理论,即只有在粘性底层附近产生纵向涡,才能实现同功耗下湍流对流强化。本文计算入口速度型粘性底层和过渡层的总厚度约为0.004 2m,即陷窝深度约为粘性底层和过渡层的总厚度的1.2倍,见图2。

图1 计算模型示意图Fig.1 Computational model

图2 陷窝前速度型和陷窝截面图Fig.2 Velocity profile before dimple
模型侧面为对称面,布置陷窝底板及陷窝为无滑移物面。为消除入口段影响,计算入口边界设为充分发展边界条件。入口边界条件为速度入口。初始速度均匀分布为4m/s。通过流量守恒迭代得到流动充分发展入口速度(图3),湍流强度分布如图4。出口边界条件是压力出口,出口相对静压为0Pa。基于入口平均速度4m/s和两平板间距离0.2m的Re数为5.48×104。假设空气不可压缩。

图3 x方向速度分布Fig.3 x-velocity distribution

图4 湍动能分布Fig.4 TKE distribution
2 数值计算方法
2.1 数值方法
本文用Fluent进行两平板间充分发展流动定常RANS数值模拟。计算选择基于压力的求解器,速度压力耦合采用Coupled方式。湍流模拟选择k-ωSST湍流模型。k-ωSST湍流模型在壁面粘性模拟中采用增强壁面法,直接求解粘性底层的流动。动量方程,湍流强度k,比耗散率ω和能量方程的对流项离散采用三阶MUSCL格式。
2.2 计算网格
空间离散采用ICEM生成多块结构网格。尽量保持网格方向和流动方向的一致性,以及较好的正交性和较小的长宽比。如图5为整体和陷窝局部网格,为展示布置陷窝底板网格结构,隐去顶面网格。因三个面均为对称面,只需在底板法向加密网格,简化了计算模型。从图中可见对无滑移底板边界层网格进行加密。无滑移物面的法向第一个网格满足y+<1,并在粘性底层(y+<10)的区域内有多于10个网格。采用O型网格拓扑结构对陷窝前后缘和陷窝内部进行局部加密。总网格单元数为169万。

图5 模型整体和陷窝局部网格Fig.5 Model grid
在涡核处网格密度和空间离散格式精度会引起超出涡物理粘性耗散的强涡数值耗散,致使对旋涡结构的模拟不准确。为保证计算结果的准确性,在原始169万网格的基础上在研究关注的涡核附近区域加密得到269万网格。两套网格涡核轴向速度对比如图6,两套不同网格模拟得到的涡结构基本重合,即本文网格的节点布置和拓扑结构划分能够较好地模拟陷窝诱导的涡结构。

图6 不同网格计算涡核轴向速度对比Fig.6 Grid comparison of vortex core axial velocity
2.3 计算和实验对比验证
本文采用和文献[8]的设置对陷窝强化对流传热进行数值模拟,并与文献[8]的实验结果进行对比,如图7所示。光滑管道计算值为Nu0。计算与实验结果的Nu/Nu0相对误差在6%内,说明了本文数值模拟方法的可靠性。

图7 数值模拟和实验对比Fig.7 Comparison of numerical simulation and experiment
3 计算结果与分析
3.1 半涡环涡结构分析
图8所示为采用涡矢量方法所得的陷窝内涡核俯视图和侧视图。从图中可以看出:涡核呈对称分布;在两侧壁面起始段与物面垂直;上升到一定高度后,涡核沿流向发展至对称面。结合图9物面的极限流线可以看到物面极限流线流谱中奇点的分布为两个鞍点+两个分离螺旋点。分离线上奇点分布为螺旋点/鞍点/螺旋点。分离属于典型的闭式分离。物面两个对称稳定的分离螺旋点对应于空间对称的类龙卷风涡。类龙卷风涡的形成条件为物面逆流的出现,分离螺旋点的形成,以及类龙卷风的垂直涡升起。陷窝前缘的分离和迎风面的再附形成了陷窝背风面的逆流,从而形成了两个对称的分离螺旋点。物面分离螺旋点形成以后,汇聚了物面的部分涡量升起,在空间演化为垂直物面发展的类龙卷风涡。闭式分离流动具有明显的禁区性特点,给分离涡输送涡量的边界层位于闭式分离线的下游。对称类龙卷风涡的涡量由分离涡面在分离线下游卷绕涡面提供。随着涡沿流向的发展,涡核从垂直物面发展转为沿流向向对称面发展。从涡核的空间结构图可见,由对称的类龙卷风涡形成的双涡结构在对称面闭合,形成半涡环涡结构[12]。半涡环涡结构指两个涡轴端点终止于壁面分离螺旋点的半环型涡结构,陷窝内半涡环示意见图10。

图8 涡核线空间分布俯视图和侧视图Fig.8 Vortex core vertical and side view
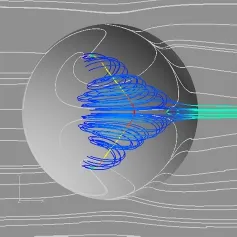
图9 物面的极限流线Fig.9 Wall streamline

图10 半涡环涡结构示意图Fig.10 Half ring vortex schematic drawing
从图11可见沿涡核轴向流动一直在逆压梯度下。在涡的起始段,逆压梯度较小;随着涡的发展,逆压梯度逐渐增加。在x=0.204至x=0.205的涡轴位置,逆压梯度增幅较大,对应于图12轴向速度减小至零,并出现轴向逆流的位置。旋涡对逆压梯度很敏感,逆压梯度的突然增加会引起旋涡的不稳定性甚至破裂,同时会带来轴向速度的减小和轴向逆流的出现。从图12可见涡轴的轴向速度最大为0.1m/s,本文计算的入口平均速度为4m/s,相对于入口速度,涡轴的轴向速度值很小。闭式分离明显的禁区性特点使得来流只能在分离线的下侧回流进入旋涡,动量输入小。
下面结合图13垂直涡轴横截面流态讨论半涡环涡结构沿流向的演变过程。图13中陷窝外主流流场流向从左向右。在x<0.202范围内,涡轴轴向速度加速度λ>0,轴向速度增加,在涡轴附近,截面流态为稳定的螺旋点形态,流线由外部指向旋涡中心,见图13(a)。类龙卷风涡结构稳定。涡核处因粘性耗散及粘性扩散损失的涡量得到流向涡轴的涡量补给,涡量平衡,旋涡稳定。在0.202<x<0.206范围内,λ<0,轴向速度减小。沿涡轴线λ变号,由正变为负,则从变号点起,其涡心附近的截面流线图上出现稳定的极限环,即出现Hopf分叉,见图13(b)。稳定极限环外部流线由外部指向极限环,流动稳定;稳定极限环内部为不稳定的螺旋点形态,流线由旋涡中心指向旋涡外部。即旋涡的不稳定最先出现在涡轴附近。随着流动沿着涡轴的发展,极限环逐渐变大,不稳定区域也逐渐变大,见图13(c)。在x=0.204位置,极限环消失,不稳定区域占据了全部的分离区域,见图13(d)。在x=0.205 4位置,截面流线拓扑结构保持不变,见图13(e)。直至x>0.206时,轴向速度加速度λ>0,沿涡轴线λ变号,由负变为正,则从变号点起,其涡心附近的截面流线图上开始出现不稳定的极限环,极限环内部出现稳定螺旋点。在0.206 6位置时,稳定螺旋点已经占据了较大的空间,见图13(f)。

图11 轴向压力分布Fig.11 Vortex core pressure distribution

图12 轴向速度分布Fig.12 Vortex core axial velocity distribution

图13 垂直涡轴横截面流线图Fig.13 Slice streamline vertical to vortex core
数值模拟结果中的截面拓扑结构变化规律以及极限环的产生与张涵信的拓扑分析定性分析理论是相符的,说明了本文数值模拟结果和分析结果的正确性。
3.2 半涡环涡破裂
如图14空间流线图可见在涡轴与x=0.205相交处布置种子,计算所得空间流线图。可见在x=0.205位置之前紧紧绕涡核旋转流动的流线突然扩张,旋涡破裂。且由图8涡核0.205处轴向速度降为零,同时压力梯度增幅陡增。由图9涡核空间俯视图可见,半涡环涡核在对称面出现拐折。涡环受到扰动后,失去稳定性,圆环变成多边形形状[13]。作为半涡环,涡核出现较明显的夹角状态意味着半涡环失稳。从图13垂直涡轴截面流线演变过程可见,在0.205位置不稳定螺旋点已占据了绝大部分区域,旋涡不稳定。由涡破裂理论知,此处涡破裂,其破裂的起点为驻点。涡破裂的主要特征是旋涡的轴向速度迅速下降,形成内驻点,驻点后为回流区,涡核半径突然扩张,形成一个近似轴对称的破裂泡[10-11]。
从λ>0到λ<0,由λ=0的位置起,横截面流线出现Hopf分叉产生稳定的极限环。该极限环的边界,将流动分成内外两区,外区截面流线由外向内转而指向极限环;内区是不稳定的,截面流线由涡心向外转而指向极限环。这就是说,旋涡的失稳,首先发生在涡轴附近。这样,涡轴附近处于不稳区的流体,在向前运动且不断减速的过程中,就可能因失稳而破裂。根据旋涡沿轴线的非线性分叉理论[11],当破裂点出现在轴向速度为零的位置时,其纵向截面流线为鞍点形态,如图15所示,则说明在x=0.205破裂类型为泡型破裂。

图14 过涡核驻点的空间流线Fig.14 Streamline through stagnation point

图15 过涡核驻点纵向截面鞍点流态Fig.15 Slice streamline align to vortex core through stagnation point
一般旋涡的运动分区为粘性起主导作用的涡核区和涡核外近似无粘准自由涡区[14]。准自由涡区为涡核半径以外的区域,此处流体的运动近似为无粘流,主要由压力场决定,基本不受粘性力的作用,所以总压变化幅度不大。即在准自由涡区,存在压力梯度,但总压梯度基本为零。粘性主导涡核区为从最大涡核半径处到轴心,切向速度从峰值迅速减小到零,就像边界层的速度型,从边界层顶部的速度很快降低到零。涡核区域是粘性高度集中的区域,由粘性力和压力共同作用,由于粘性耗散,使涡核区域处总压损失,有较大的总压梯度。因此,从流场的低总压分布区域和总压梯度较大的区域可以准确地划定有强粘性耗散的涡核区域。从半涡环总压切片图16可以看到涡核处总压从开始有较大的梯度到梯度逐渐变小,直到0.204截面总压最小值超出了所绘制云图的上限,低总压区逐渐消失,即强粘性耗散区逐渐消失。涡核尺寸在粘性扩散的作用下逐渐增大,涡核强度在粘性耗散和粘性扩散的共同作用下逐渐变弱,以致破裂。

图16 涡核处总压等x切片图Fig.16 Equal xslice total pressure distribution
以上种种证实了半涡环在x=0.205位置涡破裂的事实。
从已发表文献[1-9]中展示的流场结构中可见,Isaev[1-3]和谢永惠[5]的数值模拟结果中都显示出螺旋点/鞍点/螺旋点的闭式分离,两个对称的物面螺旋型焦点对应于空间旋涡的物面起始点,和本文的数值模拟结果一致。
本文认为同样是物面两个对称的螺旋型焦点在空间里可能形成两个完全不同的涡结构。如果涡核在对称面闭合,涡结构应为两个涡轴端点终止于壁面的半涡环涡结构;如果涡核在对称面不闭合,沿流向延伸,则涡结构应为双单元类龙卷风涡。本文数值模拟的陷窝内涡结构定义为中间失稳破裂的半涡环较合理。
3.3 旋涡对陷窝后流场影响
如图17为陷窝后等x截面流线图。从图中可以看到陷窝后流体有纵向旋转的趋势。这是陷窝内的半涡环破裂后涡量在下游流场中分散分布的结果。旋涡破裂后涡核内的集中涡量分散开来,随着流体的向后流动向下游输运,形成陷窝后的涡量分布,并诱导陷窝后流体横向流动。图中贴近物面的截面流线旋涡是陷窝前缘分离流体在陷窝迎风面再附后部分流体向后绕尖后缘流动形成的对称的边涡对。主涡对破裂涡量在空间散开,分布空间较大,涡量强度较小,诱导形成陷窝后弱纵向涡;边涡对紧贴物面形成,分布集中,涡量强度较大。它们旋转方向相同,共同形成对陷窝后流场的扰动,加强了陷窝后流场的对流强度。刘高文[8]也试验研究发现气流经过陷窝后诱导形成一对尺寸较大的旋涡附着于尾迹区。

图17 陷窝后纵向涡截面流线Fig.17 Wake longitudinal vortex slice streamline
4 结 论
本文对布置深宽比为0.2陷窝两平板间充分发展段流动进行了数值模拟,利用张涵信的旋涡沿轴线的非线性分叉理论和沿涡轴的轴向速度和压力分布等细致分析在稳态假设下陷窝内涡结构发展、演变及破裂的规律。主要结论为:
(1)对于物面流线有两个螺旋型焦点的陷窝内流动,当涡核在对称面闭合,涡结构应为半涡环;当涡核在对称面不闭合,涡结构应为双单元类龙卷风涡。
(2)本文数值模拟陷窝诱导的涡结构为中间失稳破裂的半涡环结构。半涡环结构由对称的类龙卷风涡在对称面闭合形成。物面分离流谱为典型的螺旋点/鞍点/螺旋点分离。螺旋分离点为类龙卷风涡在物面的起始点。物面分离螺旋点形成后,汇聚了物面的部分涡量升起,在空间演化为垂直物面发展的类龙卷风涡。
(3)半涡环的发展经历了从垂直于物面稳定升起,截面流线在涡心附近从稳定的螺旋点形态;涡心附近出现不稳定的螺旋点形态;再到涡泡型破裂的过程。半涡环经过了稳定升起,沿流向随着涡量粘性扩散和涡核的粘性耗散下变得不稳定,最后在强逆压梯度下泡型涡破裂的过程。
(4)半涡环涡破裂涡量散开诱导形成陷窝后的弱纵向涡,和陷窝尖后缘绕流产生的边涡旋转同向,加强了陷窝后流场的对流强度。
[1]Isaev S A.The effect of rearrangement of the vortex structure on heat transfer under conditions of increasing depth of a spherical dimple on the wall of a narrow channel[J].High Temperature,2003,41(2):229-232.
[2]Isaev S A.Numerical simulation of vortex enhancement of heat transfer[J].High Temperature,2003,41(5):665-679.
[3]Isaev S A.Influence of the Reynolds number and the spherical dimple depth on turbulent heat transfer and hydraulic loss in a narrow channel[J].International Journal of Heat and Mass Transfer,2010,53:178-197.
[4]Turnow J,Kornev N,Isaev S A.Vortex mechanism of heat transfer enhancement in a channel with spherical and oval dimples[J].Heat and Mass Transfer,2011,47(3):301-313.
[5]LAN Jibing,Xie Yonghui,Zhang Di.Large eddy simulation for control of boundary layer separation with dimples,Journal of Xi’an Jiaotong University,2010,44(9):27-32.(in Chinese)蓝吉兵,谢永惠,张荻.采用球窝控制边界层分离流动的大涡模拟[J],西安交通大学学报.2010,44(9):27-32.
[6]Qiao Weiyang.Control of separation losses on turbine blade with low Reynolds number[J],Journal of propulsion technology,2005,26(1):42-45.(in Chinese)乔渭阳.低雷诺数涡轮流动损失控制技术 [J],推进技术.2005,26(1):42-45.
[7]Liu Gaowen.Review of heat transfer enhancement for dimpled surface[J].Journal of Aerospace Power,2007,22(11):1785-1791.(in Chinese)刘高文.凹坑强化传热的研究进展回顾[J].航空动力学报,2007,22(11):1785-1791.
[8]Liu Gaowen.Transient infrared heat transfer measurements and surface flow visualization on a single dimpled wall[J].Journal of Propulsion Technology,2009,30(1):41-45.(in Chinese)刘高文.单凹坑壁面的瞬态红外传热测量与流场显示[J].推进技术,2009,30(1):41-45.
[9]Li Rui,He Yaling.Numerical simulation of dimpled tubes for heat transfer enhancement[J].Journal of Engineering Thermophysics,2008,29(11):1947-1949.(in Chinese)李瑞,何雅玲.丁胞型强化换热管的数值模拟[J].工程热物理学报,2008,29(11):1947-1949.
[10]Zhang Hanxin,Deng Xiaogang.Analytic studies for three dimensional steady separated flows and vortex motion[J].Acta Aerodynamica Sinica,1992,10(1):8-20.(in Chinese)张涵信,邓小刚.三维定常分离流和涡运动的定性分析研究[J].空气动力学学报,1992,10(1):8-20.
[11]Zhang Hanxin.Bifurcation of vortex motion along its axis[J].Acta Aerodynamica Sinica,1994,12(3):242-251.(in Chinese)张涵信.旋涡沿轴线的非线性分叉[J].空气动力学学报,1994,12(3):242-251.
[12]Wang Xiaoxin,Wu Ziniu.Study on wake vortex influence in insect flapping hovering flight[D].[PhD Thesis].Beijing:Tsinghua University,2012.(in Chinese)王晓欣,吴子牛.昆虫扑翼悬停飞行尾涡影响研究[D].[博士学位论文].北京:清华大学,2012.
[13]Tong Bingang.Unsteady flow and vortex motion[M].Beijing:National Defence Industry Press,1993.(in Chinese)童秉纲.非定常流与涡运动[M].北京:国防工业出版社,1993.
[14]Xia Xuejian,Deng Xueyin.Engineering separation dynamic flow[M].Beijing:Beihang University Press,1991.夏学湔,邓学蓥.工程分离流动力学[M].北京:北京航空航天大学出版社,1991.
[15]Wang Gang,Liang Xingang.Tornado-like vortices generation and its aerodynamic characteristics[J].Acta Aerodynamica Sinica,2005,23(2):167-172.(in Chinese)王刚,梁新刚.羊角涡结构及其特性[J].空气动力学学报,2005,23(2):167-172.
[16]Wu Jiezhi.Introduction to vorticity and vortex dynamics[M].Beijing:Higher Education Press,1993.(in Chinese)吴介之.涡动力学引论[M].北京:高等教育出版社,1993.
[17]Jeong J H,Hussain F.On the identification of a vortex[J].J.Fluid Mech.,1995,(285):69-94.

