民用飞机机身表面静压孔气动布局设计研究
孙一峰,杨士普,*,方 阳,陈迎春,2
(1.中国商用飞机有限责任公司 上海飞机设计研究院,上海 201210;2.中国商用飞机有限责任公司,上海 200120)
0 引 言
现代民用飞机依赖于先进的大气数据系统,通过安装于飞机外部的传感器或探头感知探测周围大气状况,进而计算获得飞机运行所需的大气数据,提供给机组和相关机载系统使用。目前一类典型民机使用的大气数据传感器组合包括有静压孔、皮托管、风标和总温探头,分别用于测量气流的静压、总压、攻角和总温,这些原始测得量经由大气数据计算机修正处理后得到气压高度、校正空速、真空速、飞行马赫数、飞行迎角等真实反映飞行器当前状态及姿态的大气数据。本文研究的机身表面静压孔是一种以镶嵌方式平齐地安装于机体外表面的静压测量装置,常见于现役的大中型亚声速民用运输类飞机(图1标示了目前航线运营的空客A320飞机的大气数据传感器分布情况,其中也标示了所使用的机身表面静压孔)。

图1 现役空客A320飞机机身表面大气数据传感器Fig.1 Sensors and probes on current A320in service
大气数据的准确性对飞行员安全操控驾驶飞机的重要性不言而喻。此外,作为现代民用飞机核心航电系统的重要组成部分,大气数据系统还将直接影响飞控系统、自动驾驶系统、导航系统、发动机控制系统等以大气数据作为输入的关键子系统[1]。对民用飞机主制造商而言,围绕如何获取准确、可靠的大气数据,相关工作伴随需求论证、方案设计、系统集成、试飞验证、适航取证等一系列过程。以本文所要研究的静压孔为例,其测量静压直接影响到气压高度的获取精度,并间接影响校正空速、飞行马赫数等其他大气数据信息,相应的系统测量误差要求在运输类飞机适航标准中均有所规定。对民用飞机航线运营和空中交通管理尤为重要的高度层垂直间隔严重依赖于气压高度的获取精度,适航条款中关于飞行器在缩小垂直间隔(Reduced Vertical Separation Minimum,简称RVSM)空域的运行要求为当前静压系统设计提出了最为苛刻的误差控制要求[2-3]。
过去国内外已有不少文献资料飞行器静压测量校准进行了研究,涉及了误差源分析、测量装置选取、安装定位、试飞校准等方面的工作[4-8]。机体表面静压孔的目标测量量是与飞机所处高度层相对应的环境静压(无干扰来流静压),其直接测量值与环境静压的差常被称之为静压孔的位置误差。静压孔位置误差主要受静压孔在机体表面安装位置的影响,机体外形引起的气流畸变是导致当地静压偏离环境静压的内在原因,因此从气动角度出发进行静压孔布局定位的首要原则是尽可能减小和控制其位置误差[9-10]。在表面静压孔的定位原则方面,几个文献中均提及了图2[10-12],它反映了沿地板线方向机体表面静压偏离环境静压的趋势,其中与横轴的交点表明当地静压与环境静压相同,理论上是理想的静压孔布置位置。
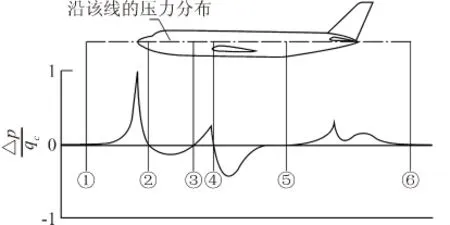
图2 典型亚声速飞机机身静压分布Fig.2 Typical subsonic pressure distribution on an aircraft fuselage
值得注意的是,图2仅反映了飞机在某一特定飞行条件下的静压分布,但其包含的信息在设计实践中并不足以具体指导静压孔的布局方案。由于机体表面静压分布的复杂性,加之飞行工况,乃至飞机构型变化(如襟翼、起落架收放等)均可能对机身静压场产生显著影响。静压孔位置的选定往往需要经过一系列模型风洞试验验证,并最终经过试飞确认[12]。如今得益于CFD技术在飞机设计中日益广泛的应用[13-14],使得本文可以充分借助CFD工具的优势,研究典型民机在更大飞行包线内的机体静压分布规律,进一步探索总结静压孔的气动布局定位原则,以便更好的服务于静压系统的初步设计,降低后期飞行验证的风险。
1 问题分析
为了定量衡量表面静压孔的位置误差,本文将定义并利用静压恢复系数pratio表征机身表面某处当地静压偏离环境静压的程度:

其中ps为当地静压,pa为环境静压。
利用量纲分析容易知道任意位置的静压恢复系数pratio是仅依赖于飞行马赫数Ma、飞机迎角α、飞机侧滑角β、飞行雷诺数Re,普朗特数Pr的函数[15],可以表示为:
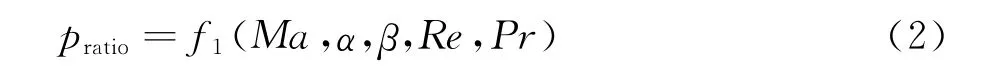
针对我们的研究的亚声速民机范畴内,Pr数可认为是常量。对于适合静压孔布置的大部分机身区域,其边界层厚度不是很大,Re数不会显著影响pratio。此外考虑飞机的实际侧滑大小对静压影响较小,常用的静压孔的双侧布置可基本消除这种影响。因此上述关系可以进一步简化为:

这表明静压孔的位置误差主要受飞行马赫数和迎角影响。考虑到静压测量要求具备很高的可靠性和重复性,且应易于建立获取修正规律,因此从气动布局的角度出发,静压孔应布置在机身上静压恢复系数随马赫数和迎角变化不敏感的区域。
2 CFD计算与分析
本节考虑某典型现代民机巡航构型的速度迎角包线,选取表1所示的马赫数、迎角组合状态,通过CFD计算较为完整地研究机身静压场,获得机身静压随马赫数和迎角的变化规律。
本文计算使用了商用CFD软件ANSYS CFX。CFX是一个格点有限体积法的通用CFD求解器,它采用基于压力的全隐式离散格式,使用耦合代数多重网格技术求解三维Navier-Stokes方程。本文在网格生成方面采用ICEM CFD生成非结构化网格,但未在物面边界层区域进行额外的棱柱网格剖分,为全空间的四面体网格,该网格策略对于机身静压分布计算是合适且高效的。图3显示了机身表面网格,考虑到工程实际,外翼部分也被略去,且在关注的区域进行了加密。

表1 马赫数、迎角状态点Table 1 Mach number and AOA combinations

图3 简化计算模型的表面网格示意图Fig.3 Surface mesh of a simplified aircraft model
为了更定量直观的呈现静压孔位置误差对马赫数和迎角的敏感度,本文将CFD计算结果作为目标统计量进行进一步后处理。固定马赫数,将同一位置不同迎角下的结果作为一组统计样本,计算其样本方差,可以反映迎角变化时对应结果的离散度。同样的,固定迎角,也可以得到马赫数改变的一组结果的样本方差。按照该思路,2.1节和2.2节将分别研究静压恢复系数对迎角和飞行马赫数变化的敏感度。
2.1 静压恢复系数对迎角变化的敏感度
CFD计算结果分析常绘制压力系数分布云图,其中压力系数的定义为:

其中ρ和Va为无穷远处无干扰来流的密度和速度,结合马赫数定义和理想气体状态方程,可推出静压恢复系数pratio满足如下关系:
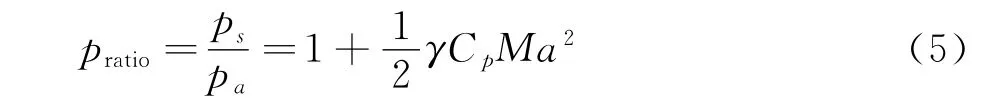
上式正是公式(3)反映的函数关系的具体化。
至此,pratio随迎角的变化的敏感度(固定马赫数)可使用同一位置不同迎角下一组Cp结果的离散度来衡量。选取表1中任一马赫数下CFD计算得到的一组Cp结果进行处理,绘制出该马赫数下的Cp样本方差分布云图,该云图将直观定量显示机身表面pratio对迎角变化的敏感度。这里仅给出了对应马赫数0.4、0.6、0.785的结果(图4至图6)。

图4 Ma=0.4时Cp值样本方差云图Fig.4 Variance contour of Cp(Ma=0.4)
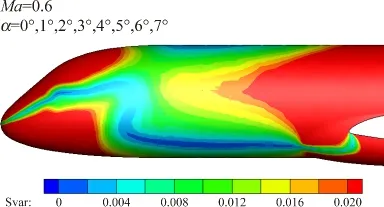
图5 Ma=0.6时Cp值样本方差云图Fig.5 Variance contour of Cp(Ma=0.6)

图6 Ma=0.785时Cp值样本方差云图Fig.6 Variance contour of Cp(Ma=0.785)
2.2 静压恢复系数对飞行马赫数变化的敏感度
同样根据公式(5),pratio对马赫数变化的敏感度(固定迎角)可使用同一位置不同马赫数下一组CpMa2结果的离散度来衡量。选取表1中某一迎角下的一组CFD结果,绘制出该迎角下CpMa2值的样本方差分布云图,该云图即显示了机身表面pratio对飞行马赫数变化的敏感度。这里仅给出了对应迎角2°、4°和6°情形下的结果(图7~图9)。

图7 α=2°时CpMa2值的样本方差云图Fig.7 Variance contour of CpMa2(α=2°)

图8 α=4°时CpMa2值的样本方差云图Fig.8 Variance contour of CpMa2(α=4°)
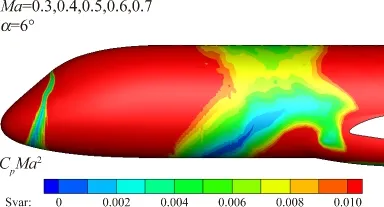
图9 α=6°时CpMa2值的样本方差云图Fig.9 Variance contour of CpMa2(α=6°)
2.3 结果讨论
从图4至图6中可以看到,在给定马赫数下,前机身均明显存在有Cp值样本方差接近于零的区域,该区域总是规律性的呈条带状从机头延伸至翼身整流罩,该区域内pratio将几乎不随迎角变化而改变。同样,图7至图9显示,在给定迎角下,机身上也能找到CpMa2值,亦即pratio随马赫数改变不发生显著变化的区域。但相比于迎角变化的不敏感区,该马赫数变化不敏感区的分布范围较窄,区域规则性及随迎角变化时的规律性相对较差。
如果将表面静压孔理想的布置在pratio对迎角和马赫数变化均不敏感的区域,则可选区域受限较多,考虑实际机体结构或其他设备布置的限制,实际工程操作的可行性更差。此外由于静压修正规律的获取和确认最终需要经过试飞,而试飞过程中迎角的获取精度要远低于马赫数的获取精度,那么保证静压孔测量结果对迎角变化不敏感的特性则更具实际工程意义。
综上,在初步设计阶段静压孔的气动布局定位将首先考虑静压恢复系数pratio对迎角变化的不敏感,2.1节中所示的条带状不敏感区宜于作为表面静压孔的定位布置基线,其中敏感度的定量判据需要通过静压系统顶层设计要求分解及静压误差分配进一步细化,本文对此不做展开。
3 风洞试验
在利用第2节方法得到静压孔可行布置区域的基础上,综合考虑气动之外的其他约束,可给出机身静压孔的初步位置方案,之后进一步通过风洞试验进行方案验证及修正曲线获取。
图10显示了某型民机的大气数据传感器风洞试验。试验中除去在静压孔安装位置上布置了测压孔,出于对比考虑还另外在位置1、2处沿横截面周向另外布置了一系列测压孔,这样既能验证静压孔气动布局方案,又可以检验上文得到的静压孔的气动布局定位原则。

图10 某型民机大气数据传感器布局风洞试验Fig.10 Wind tunnel test for airdata system
图11~图12分别给出了位置1、2处测压孔在风洞试验的马赫数和迎角组合范围内pratio的变化规律,并且比较了基于风洞试验模型的CFD计算结果,可以看到风洞试验与CFD计算的规律趋同,量值吻合度较高。此外,位置1、2处的测压数据显示了其静压恢复系数pratio随迎角变化不敏感,随马赫数变化规律较为简单,从气动角度考虑是较为理想的表面静压孔布置位置。

图11 位置1处pratio的风洞试验与CFD计算结果Fig.11 WT and CFD results for pratioat location 1

图12 位置2处Pratio的风洞试验与CFD计算结果Fig.12 WT and CFD results for pratioat location 2
4 结 论
本文以某型现代民机的机身表面静压孔气动布局设计工作为背景,借助CFD计算研究了该型民机在不同马赫数和迎角组合下的机身静压场,CFD结果的统计后处理显示机身表面规律性的存在静压恢复系数对迎角变化不敏感的条带状区域。该不敏感区适宜作为初步设计阶段机身表面静压孔布局定位的参考基线,基于上述原则选取的静压孔初步安装位置在风洞试验中得到了验证。
本文提出的一种基于CFD计算及其结果统计后处理的表面静压孔辅助定位方法,相比于传统方法,本文方法能够直观且定量的给出机身表面可行的静压孔布置区域,具备实际应用价值,对解决类似工程问题具有较好的借鉴意义。
[1]Collinson R P G.Introduction to avionics systems[M].Springer,2011.
[2]CAAC.CCAR 25-R3Chinese civil aviation regulations part 25:transport category airplane airworthiness standards[S].2001.中国民用航空局.CCAR 25-R3中国民用航空规章第25部:运输类飞机适航标准[S].2001.
[3]AC 25-7C.Flight test guide for certification of transport category airplanes[S].Federal Aviation Administration,2012.
[4]Gracey W.Measurement of aircraft speed and altitude[R].NASA Langley Research Center,Hampton,VA,1957.
[5]Gracey W.Measurement of static pressure on aircraft[M].National Advisory Committee for Aeronautics,1957.
[6]ADA320216.Pitot-Statics and the Standard Atmosphere[S].USAF Test Pilot School Document,1996.
[7]Huston W B.Accuracy of airspeed measurements and flight calibration[R].NASA,Washington DC,1948.
[8]Qian Guoyu.Static source error correction and its application in air data computers[J].Chinese Journal of Aeronautics,1989,10(4):171-179.钱国宇.静压源误差修正及其在大气数据计算机的应用[J].航空学报,1989,10(4):171-179.
[9]Gudmundsson S.General aviation aircraft design:applied methods and procedures[M].Butterworth-Heinemann,2013.
[10]Haering E A,Jr.Airdata measurement and calibration[R].NASA Technical Memorandum 104316.National Aeronautics and Space Administration,Dryden Flight Research Center,1995.
[11]Brow E N.Position error calibration of a pressure survey aircraft using a trailing cone[R].20th Society of Flight Test Engineers,Annual Symposium.Reno,NV.1989.
[12]Wuest W,et al.Pressure and flow measurement-flight testing[R].AGARD-AG-160,Vol.11,1980.
[13]Deng Jian,Lyu Lingying.CFD Application in pitot-static tube error correction and its validation in wind tunnel test and flight test[C].2ndModern Experimental Aerodynamics Conference,Harbin:2009.邓建,吕凌英.空速管静压源误差修正的CFD方法及风洞实验与试飞验证技术研究[C].第二届近代实验空气动力学会议,哈尔滨:2009.
[14]Johnson F,Tinoco E N,Yu N J.Thirty years of development and application of CFD at Boeing commercial airplanes,Seattle[J].Computers &Fluids,2005,34(10):1115-1151.doi:10.1016/j.compfluid.2004.06.005
[15]Herrington R M.,et al.Flight test engineering handbook[M].Air Force Flight Test Center Edwards AFB CA,1966.

