基于自由涡方法的风轮偏航气动特性研究

仇永兴，康 顺

（1.华北电力大学电站设备状态检测与控制教育部重点实验室，北京 102206；2.西安现代控制技术研究所，陕西西安 710065）

基于自由涡方法的风轮偏航气动特性研究

仇永兴1，＊，康 顺1，2

（1.华北电力大学电站设备状态检测与控制教育部重点实验室，北京 102206；2.西安现代控制技术研究所，陕西西安 710065）

采用非线性升力线方法和时间精确自由涡方法，对风切变条件下风轮的偏航气动特性进行了非定常数值模拟。为了改善非线性升力线方法的计算收敛性，提出了基于Newton-Raphson方法的环量方程迭代算法。建立了一种包含粘性涡核并由自由涡面和叶尖涡线构成的改进尾迹模型，可以提高尾迹的计算精度和效率。以NREL Phase VI风力机和Tjreborg风力机为算例，分别对均匀风和切变风条件下、风轮处于不同偏航角时的气动力进行计算，并与测量值进行了比较。分析了风切变和偏航风对风轮气动特性产生影响的主要因素及风轮气动特性的变化规律。结果表明：计算方法可以有效模拟风切变条件下风轮偏航气动特性；在风切变条件下，偏航会增加叶片扭矩的波动，当风轮处于正偏航角时，叶片挥舞力矩的波动减弱，处于负偏航角时，挥舞力矩波动增强。

风轮；风切变；偏航风；非定常模拟；自由涡

0 引 言

风力机运行在风速、风向不断变化的风场中。由于大气边界层的作用，来流风存在垂直风切变。在处于偏航和风切变条件下，风轮叶片会受到较复杂的非定常气动载荷，影响叶片疲劳寿命与安全。对风轮偏航气动特性的研究，常基于均匀风假设［1-3］。因此，研究风切变条件下风轮偏航气动特性具有十分重要且实际的工程意义。

基于URANS方程的CFD（Computational Fluid Dynamics）方法用于研究复杂来流条件下风轮的气动载荷模拟，仍然存在计算成本过高的问题。当前工业领域应用最为广泛的方法仍然是基于叶素动量理论的相关方法。这些方法的主要缺点是假设条件多，大量依靠经验模型。特别是使用动量尾迹模型过度简化了风轮尾迹运动，不能准确模拟复杂来流条件下尾迹的运动，从而造成诱导速度计算不准确，严重影响计算精度［4］。

基于势流假设的自由涡方法，使用环量沿径向连续变化的附着涡线模拟叶片的气动效应；用沿着叶片径向分布的尾涡线和脱体涡线模拟叶片的尾迹.随着风轮的转动，形成螺旋形的叶片尾迹。假设尾迹涡线沿着流线方向自由运动，其空间位置是流场解的一部分，由来流条件和涡线的相互扰动作用共同决定。自由涡方法已经在直升机旋翼数值模拟领域取得丰富成果［5-6］，并在风力机数值模拟领域快速发展［7-10］。其优势在于假设条件少，能够模拟叶片和尾迹的运动过程［11］，并解出流场和叶片的非定常气动载荷。相较于叶素动量理论，自由涡方法更接近物理实际，同时在计算量和计算时间上又显著少于CFD方法。

自由涡方法包括叶片气动计算和涡尾迹计算两部分。叶片气动计算常采用非线性升力线方法。由于使用翼型气动实验数据计算附着涡环量，计入了叶片边界层及分离流动的粘性效应，因此计算更加准确。由于该方法常使用简单迭代算法求解环量的非线性方程［7］，导致环量迭代不易收敛。

涡尾迹计算是通过求解涡线运动的控制方程，得到涡尾迹的瞬时空间位置。常用的方法有二阶龙格库塔方法［7，10］（2nd-order Runge-Kutta scheme，RK2）和预测-校正二阶向后差分（Predictor-Corrector with 2nd-ordor Backward difference scheme，PC2B）的时间精确解法。Leishman等的研究表明，PC2B方法在计算精度和数值稳定性上优于其他方法［12］。但是该方法的计算量大、效率低。因此，需要简化涡尾迹模型，降低计算量。常将风力机尾迹简化为由叶尖涡线构成的尾迹［13］，使尾迹模型中不包含脱体涡，降低了尾迹的计算精度。

为了解决上述问题，改进了自由涡的求解方法。为了改善采用非线性升力线方法中环量方程迭代收敛性，提出了一种基于Newton-Raphson方法的非线性环量方程迭代算法。为了提高时间精确自由涡方法的计算精度和效率，提出了一种由自由涡面（包含尾涡线和脱体涡线）和叶尖涡线构成的简化涡尾迹模型。以NREL Phase VI两叶片失速型风力机［14-15］和Tjreborg三叶片兆瓦级风力机［16］为例，分别对均匀来流和风切变条件下，风轮处于不同风速和偏航角时的气动力进行了计算，并与测量值进行比较。分析了风切变和偏航对风轮气动特性产生影响的主要因素。研究了风切变条件下，风轮不同偏航角时，气动特性的变化规律。结果表明，所建立的改进自由涡方法具有较高的计算精度和计算效率，能够有效模拟风切变条件下风轮偏航气动特性。该方法对于推动风力机的工程计算及优化设计都具有重要而且实际的意义。

1 研究方法与数值模型

1.1 非线性升力线方法

叶片的气动效应使用非线性升力线方法模拟。将叶片简化为一根环量阶跃变化的附着涡线（升力线）位于叶片翼型的1/4弦长处。由于气动力沿叶片径向的变化，环量也相应地变化。依据Helmholtz定律和Kelvin定律，升力线的环量沿叶片径向变化会产生尾涡线，随时间发生变化会产生脱体涡线。尾涡和脱体涡从叶片尾缘流向下游。因此，在叶片上附着涡线、尾涡线和脱体涡线构成涡环，如图1所示。

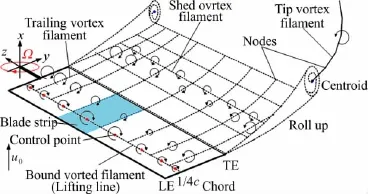
图1 叶片微段的局部坐标系及涡系构成示意图Fig.1 Schematic of blade element coordinate and vortex system composition

依据Joukowski升力定理，叶片微段上附着涡线段产生的升力为：

也可由翼型升力系数计算叶片微元段的升力，即：

其中，ГB是叶片微段的附着涡环量；u是叶片微段的合速度，包括来流风速、叶片旋转线速度、叶片附着涡段中点的扰动速度。扰动速度通过Biot-Savart定律解出，方法参见文献［10］；c是叶片微段的当地弦长；CL是翼型升力系数，可由实验或CFD数据获得，隐含了边界层及边界层分离的影响。联立式（1）和式（2）可构建求解附着涡环量ГB的方程，常采用线性迭代法求解［7］。

由于环量方程是非线性方程，使用线性迭代法往往造成解的震荡甚至不收敛。为了提高解的精度和数值稳定性，构建了基于Newton-Raphson方法的非线性方程迭代算法。将环量方程写为：

其中，f是一个趋近于0的小量；n表示附着涡微段序号。环量计算过程为：

（i）给定叶片和尾迹涡的初始环量和初始尾迹；

（ii）计算附着涡段中点的合速度，解出叶片攻角径向分布；

（iii）通过叶片当地翼型的气动特性曲线，得到升力系数；

（iv）解方程组（5），得到叶片附着涡环量的增量；

判断新旧环量值的最大相对误差小于0.001为收敛，若未收敛则用下式更新环量值，并返回步（ii）继续计算：

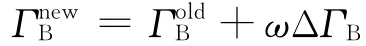
上式中，松弛因子ω推荐取0.5。方程（5）的Jacobi矩阵中的偏微分运算，使用数值微分求解。

解出附着涡环量就得到了整个涡系的环量值，同时获得叶片合速度、攻角以及气动载荷等沿径向的分布。此外，以上计算均假设叶片各微元段的绕流是二维流动，为了计入三维效应引入了Du-Selig三维失速延迟模型，见文献［17］。

1.2 自由涡计算

1.2.1 涡尾迹模型

使用时间精确算法求解尾迹涡线运动，计算精度高但是效率低。若完全满足Helmholtz定律和Kelvin定律，则需要计算尾迹中所有尾涡线和脱体涡线的运动，计算量过大，显著降低了自由涡方法的效率优势。因此，有必要简化尾迹模型。一般的方法是使用叶尖尾涡线代替整个自由涡，忽略了脱体涡的运动，降低了尾迹模型的精度。

为了有效模拟脱体涡的运动和扰动作用，并降低尾迹计算量，建立了一种由风轮附近的自由运动的涡面（包含尾涡线和脱体涡线）和较远下游的叶尖涡线构成的涡尾迹模型。模型假设：

（i）叶尖涡是由尾涡构成的集中涡。涡面运动到风轮下游一定距离后，全部卷入叶尖涡。叶尖涡涡线从涡面位于叶尖区域的卷曲中心引出，如图2所示；

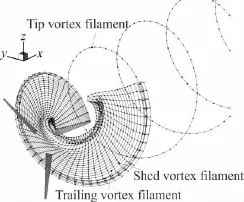
图2 风轮单根叶片的涡尾迹Fig.2 Vortex wake of one blade

（ii）尾迹中的脱体涡运动到下游一定距离后，对叶片流场的扰动作用忽略不计。所以，脱体涡只包含在自由涡面模型中；

（iii）每根涡线在运动过程中，环量值保持不变，但是涡核半径会随着运动时间和涡线拉伸率发生变化。

前两条假设，是基于流动显示实验的观察结果［18-19］，最后一条假设是基于Helmholtz涡守恒定律。为了保证流场中尾涡环量的连续性，涡面的尾涡环量需要传递给叶尖涡线。具体方法是，在两者的连接边界处，将涡面中与叶尖涡同向的尾涡环量沿着尾迹径向积分，该积分值为叶尖涡线的环量值。

为了模拟尾迹运动中的粘性效应，同时避免尾迹速度场的奇异性，在涡尾迹模型中引入Lamb-Oseen粘性涡核模型［20］：

其中：

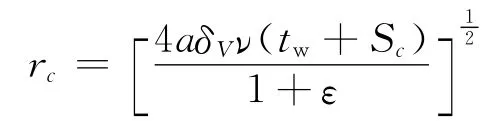
式中，a＝1.25643；涡线拉伸率ε是相邻两个时刻涡线长度的相对变化率；δV为湍流粘性系数，文献［10］指出对于小型风力机该参数一般取100，大型风力机取1000较好；Sc为涡线运动的初始时间，一般取0.5～1保证初始涡核半径rc约等于叶片平均厚度的一半。引入涡核模型后的扰动速度计算参见文献［10］。

1.2.2 涡尾迹控制方程及求解

涡尾迹由自由涡面和叶尖涡线构成。而构成自由涡面和叶尖涡线的是离散的涡线段。涡线段的运动控制方程为：

采用预测-校正二阶向后差分法（PC2B）求解控制方程（7）。式中Ψ为叶片旋转角度；ζ为风轮相对坐标系下尾迹节点的旋转幅角；Ω为风轮旋转角速度；uw为尾迹节点处流速，是风速和涡扰动速度的合速度。方程（7）离散后，得到方程（8）有：

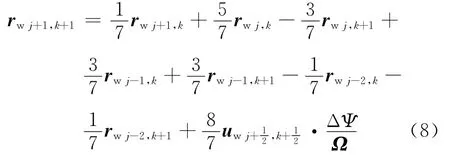
式中，j为Ψ增加方向序号；k为ζ增加方向序号。方程（8）在求解过程采用了伪隐式解法，具体解法参见文献［21］。

2 算例模型与方案介绍

为了验证计算方法的有效性，并且研究风切变条件下风轮偏航气动特性，选取以下两种风力机作为算例模型：

NREL Phase VI风力机：这是一个失速型两叶片风力机，风轮直径10.046m，叶片截面采用S809翼型。该风力机由美国可再生能源实验室设计，在NASA AMES研究中心的大型风洞中进行实验，由于实验全面且数据精确，一直作为验证风力机气动计算方法的重要参考［15］。

研究方案具体如下：

（1）方法有效性验证。NREL Phase VI风力机，风速5～12m/s，叶片桨矩角3°，无偏航，计算风力机功率和推力；风速7m/s，叶片桨矩角3°，给定风轮偏航角为10°、30°、45°和60°，计算叶片旋转一周的平均气动力。Tjreborg风力机，风速5～13m/s，叶片桨矩角0.4°，无偏航，计算风力机功率。

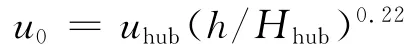
式中，uhub和Hhub分别为风轮轮毂位置的风速和轮毂高度。

3 结果与分析

3.1 方法有效性验证

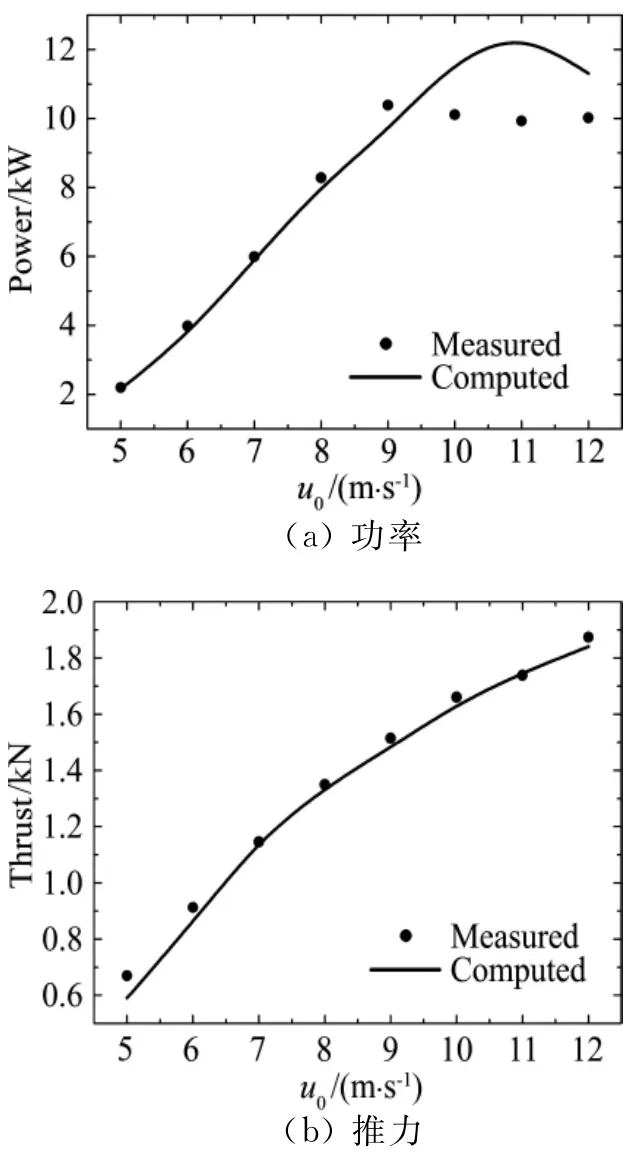
图3 功率和推力随风速的变化曲线对比，NREL Phase VIFig.3 Comparison of the computed power and the thrust with respect to the wind speed，NREL Phase VI

图3给出了均匀风条件下，NREL Phase VI风力机叶片桨矩角3°、无偏航时功率和推力计算值与实验值的比较。图4给出了均匀风条件下，Tjreborg风力机，叶片桨矩角0.4°，无偏航时功率计算值与实验值［14］的比较。

图3中可见，风速小于10m/s时，功率和推力的计算值与实验值较好吻合。当风速大于10m/s后，功率计算值与实验值误差变大，但推力仍较好吻合。主要原因是叶片已经处于失速状态，吸力面存在较强的三维分离流动［17］。计算方法受限于二维流动假设和三维失速延迟模型（Du-Selig三维失速延迟模型［17］）的计算能力，模拟叶片大分离工况存在较大误差。图4中可见，计算值与实验值很好吻合。

实验值的波动可能与实际运行中风入流存在风切变有关，下面将详细研究。

图4 功率随风速的变化曲线对比，TjreborgFig.4 Variation of the computed power with respect to the wind speed，Tjreborg

图5给出了均匀风条件下，NREL Phase VI风力机，叶片桨矩角3°，风速7m/s时，风轮处于不同偏航角时叶片法向和切向载荷系数沿径向的分布。法向和切向载荷系数的定义见文献［14］。可见，当偏航角为10°、30°和45°时，计算结果与实验数据很好吻合。当风轮处于60°偏航角时，叶片存在较大分离流动和径向二次流动，影响了计算的准确性，但是计算值在趋势上仍然与实验值保持一致，且切向力系数值与实验值吻合良好。

以上计算表明，计算方法模拟风轮气动特性是准确有效的。

3.2 风切变条件下风轮气动特性分析

为了便于分析，图7中定义了叶片方位角和偏航角。

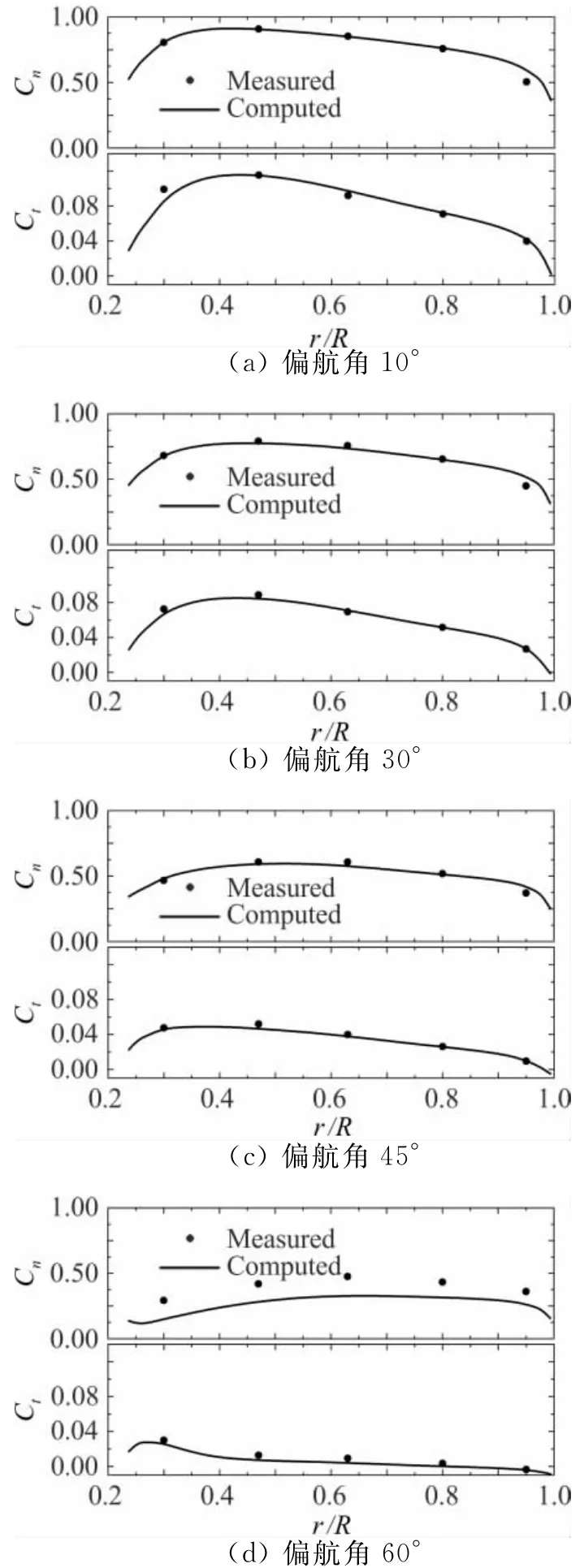
图5 给定偏航角的叶片气动力系数沿径向分布对比，NREL phase VIFig.5 Comparison of the radial distributions of the computed aerodynamic force coefficients under the yaw conditions，NREL phase VI

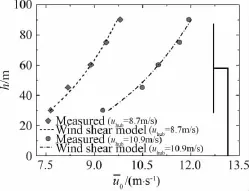
图6 风速沿高度方向的分布对比Fig.6 Comparison of the wind speed distributions in the altitudinal direction

图8中，叶片I运动到方位角约90°时，其转矩为最大值；运动到约270°时为最小值。这是因为风切变条件下，风轮上半周风速较高，下半周风速较低。当风轮无偏航时，旋转平面最高点和最低点附近分别存在叶片气动载荷的极大、极小值。

图7 叶片方位角偏航角定义示意图Fig.7 Schematic of definitions of the blade azimuth angle and yaw angle

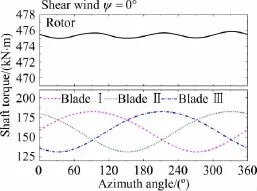
图8 风切变时风轮及叶片转矩随方位角的变化Fig.8 Variation of the computed shaft torque of the rotor and blades with respect to the azimuth angle under shear wind condition

3.3 偏航条件下风轮气动特性分析

定义叶片气动力的两个分量作为分析对象。沿着叶片径向分布的气动力，在风轮旋转方向的分量是切向力，表示为Ftangent；在风轮轴向的分量是推力，表示为Taxial。沿着叶片径向，切向力和推力分别向风轮旋转中心取矩，其合力矩分别是叶片的扭矩和挥舞力矩。定义叶片切向力系数为：叶片推力系数为：

式中，ρ为空气密度；uhub为风轮轮毂位置风速，R为风轮扫风面积。由式（9）、式（10）可见，叶片上切向力系数和推力系数的分布表示了叶片气动力在旋转方向和推力方向的分布。

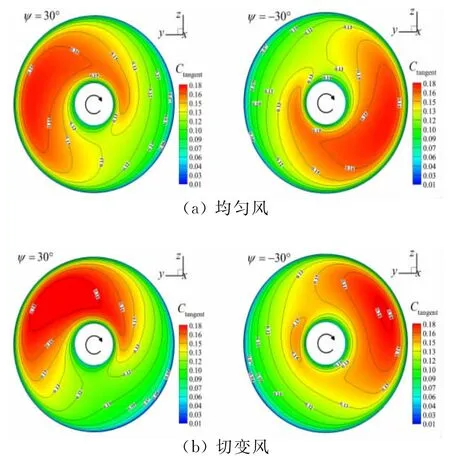
图9 不同偏航角时叶片切向力系数在旋转平面内的分布云图Fig.9 Distributions of the computed tangent force coefficient of the blade on the rotation plane under yaw conditions

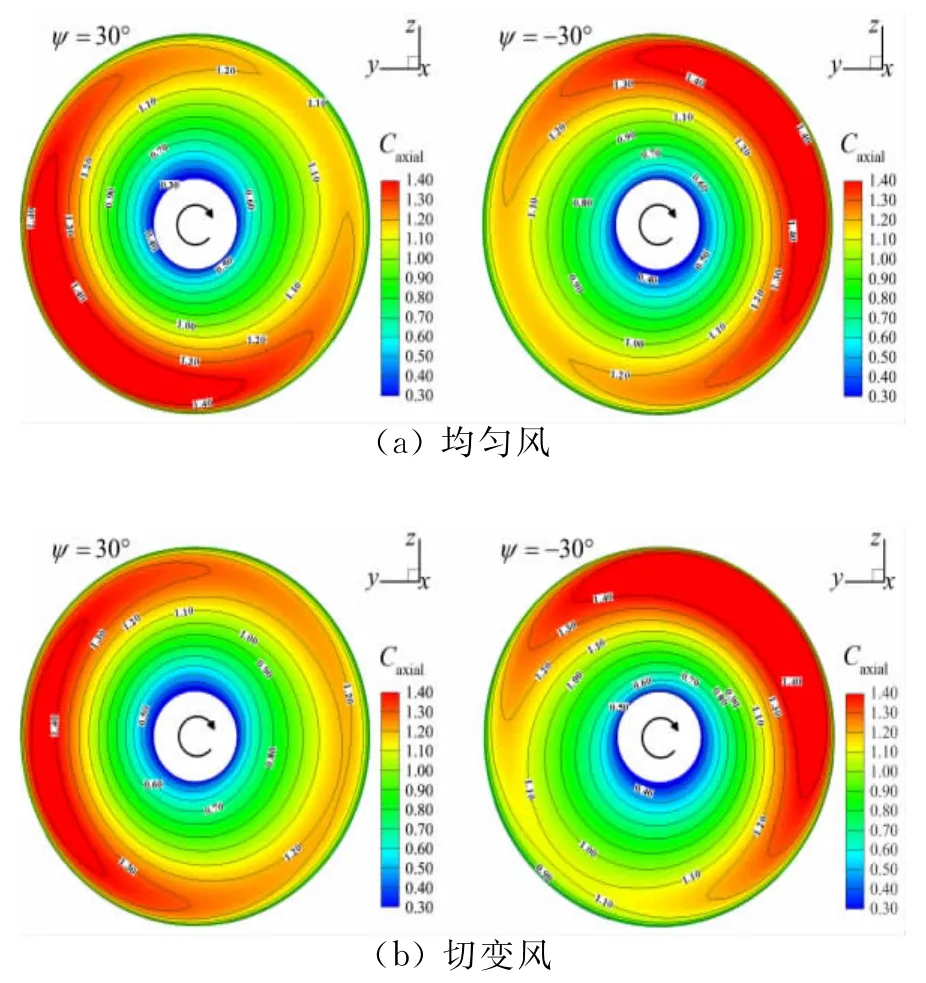
图10 不同偏航角时叶片推力系数在旋转平面内的分布云图Fig.10 Distributions of the computed axial thrust coefficient of the blade on the rotation plane under yaw conditions

图9和图10分别给出了均匀风和切变风条件下，轮毂风速10.9m/s、Tjreborg风力机处于不同偏航角时，单个叶片的切向力系数和推力系数在旋转平面内的分布云图。图中可见，偏航角相反时，均匀风条件下，气动力系数的分布呈180°中心对称；切变风条件下分布不具有对称性。随着叶片旋转，切向力系数的波动在大部分叶片半径范围内都存在，而推力系数的波动主要集中在叶片60%半径之外。

图9（b）可见，切变风条件下，正偏航时，叶片切向力系数的分布与图9（a）相比更加不均匀。其中，风轮上半周切向力系数极大值和极值区域都有所增大，风轮下半周切向力系数极小值更小，极小值区域更大；负偏航时，旋转平面内切向力系数分布相较均匀风时，极大值区域减小。当叶片运行在方位角约-120°～90°区间内，切向力系数随相位角的变化比较平缓，沿径向的分布比较均匀。

图10（b）可见，切变风条件下，正偏航时，旋转平面内推力系数的分布与图10（a）相比波动减小，推力系数的极值区域和变化幅度都有所减小；负偏航时，推力系数的波动增大。当叶片运行在方位角约45°～225°区间时，叶片半径60%以外的区域，推力系数保持在极大值。

图11给出了均匀风和切变风条件下，不同偏航角时，单个叶片的扭矩和挥舞力矩随方位角的变化对比。图中可见，与均匀风条件相比，切变风条件下，风轮正偏航时，叶片扭矩随方位角的波动明显增大。其中，扭矩极大值由方位角0°附近移动至60°附近，极小值由方位角200°附近移动至240°附近。挥舞力矩的波动明显减小；负偏航时，扭矩的波动幅值没有明显变化，但是极大值所在的方位角大约从210°变化至150°附近。挥舞力矩的波幅明显增大，极值所在方位角没有明显变化。

对图11中给出的叶片扭矩和挥舞力矩的波动规律进行定量比较：相对于均匀风条件下叶片扭矩和挥舞力矩的波幅，在切变风条件下，正偏航时，叶片扭矩的波幅增加了约57.7%（26.7kN·m），挥舞力矩波幅减小了37.8%（77.1kN·m）；负偏航时，扭矩波幅增加了10.8%（5.0kN·m），挥舞力矩波幅增加了56.6%（114kN·m）。可见，在风切变条件下，偏航风增强了叶片扭矩的波动；当风轮正偏航时，叶片挥舞力矩波动减弱，负偏航时波动增强。

图12给出了切变风条件下，偏航30°时计算得到的风轮尾迹几何。由顶视图可见，由于偏航造成尾迹在来流方向上发生偏斜运动；由侧视图可见，由于切变风造成尾迹发生上扬运动。由于偏航和切变风的共同作用，形成了结构比较复杂的风轮尾迹。

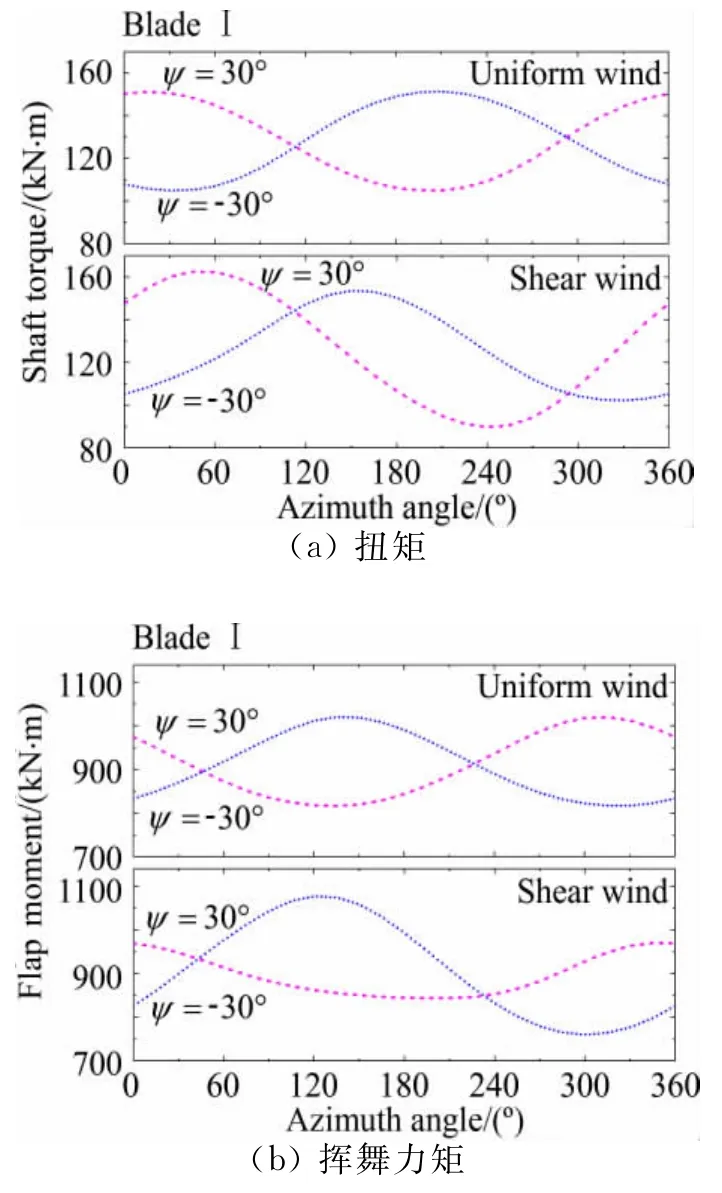
图11 不同偏航角时叶片转矩和挥舞力矩随方位角的变化对比Fig.11 Variation of the computed shaft torque and flap moment of the blade with respect to the azimuth angle under yaw conditions

图12 风轮尾迹形状，偏航30°，切变风Fig.12 Shape of the rotor wake under the condition of 30°of yaw angle with shear wind

以上研究均假设风速是定常的，风力机实际运行中，风速是非定常的。由于所研究的模拟方法属于时间步进法，因此可以将非定常风速作为数值模拟的边界条件进行研究。相关研究将会在今后的研究工作中开展。

4 结 论

基于自由涡方法，建立了一个高效模拟水平轴风力机处于风切变条件下，偏航气动特性分析的方法，并对两种不同尺度的风力机和不同运行工况进行了计算，在与实验测试数据比较的基础上，分析了风轮处于风切变和不同偏航时，叶片气动力和扭矩的变化规律。

结果表明，所建立的计算方法可以较好的模拟风切变条件下，风轮偏航时叶片气动载荷的变化。分析发现，在风切变条件下，偏航会增加叶片扭矩的波动，当风轮处于正偏航角时，叶片挥舞力矩的波动减弱，处于负偏航角时，挥舞力矩波动增强。

［1］ Tongchitpakdee C，Benjanirat S，Sankar L N.Numerical simulation of the aerodynamics of horizontal axis wind turbines under yawed flow conditions［J］.Journal of Solar Energy Engineering，2005，127（4）：464-475.

［2］ Zhou Wenping，Tang Shengli.The aerodynamic performance computation of HAWT in steady yaw［J］.Acta Energiae Solaris Sinica，2011，32（9）：1315-1320.（in Chinese）周文平，唐胜利.水平轴风力机稳定偏航气动性能计算［J］.太阳能学报，2011，32（9）：1315-1320.

［3］ Qiu Yongxing，Kang Shun.Numerical simulation of wind turbine wake based on nonlinear lifting surface method［J］.Journal of Engineering Thermophysics，2012，33（12）：2072-2075.（in Chinese）仇永兴，康顺.基于非线性升力面方法的风力机尾迹数值模拟［J］.工程热物理学报，2012，33（12）：2072-2075.

［4］ Gupta S，Leishman J G.Comparison of momentum and vortex methods for the aerodynamic analysis of wind turbines［C］.43rd AIAA Aerospace Sciences Meeting and Exhibit，Reno：2005.

［5］ Huang Shuilin，Li Chunhua，Xu Guohua.An analytical method for aerodynamic interaction of twin rotors based on free-vortex and lifting-surface models［J］.Acta Aerodynamica Sinica，2007，25（3）：390-395.（in Chinese）黄水林，李春华，徐国华.基于自由尾迹和升力面方法的双旋翼悬停气动干扰计算［J］.空气动力学学报，2007，25（3）：390-395.

［6］ Xu Bofeng，Wang Tongguang，Zhang Zhenyu，et al.Aerodynamic optimal design of winglet based on free vortex wake method and genetic algorithm［J］.Acta Aerodynamica Sinica，2013，31（1）：132-136.（in Chinese）许波峰，王同光，张震宇，等.基于自由涡尾迹和遗传算法的叶尖小翼气动优化设计［J］.空气动力学学报，2013，31（1）：132-136.

［7］ Sebastian T，Lackner M A.Development of a free vortex wake method code for offshore floating wind turbines［J］.Renewable Energy，2012，46（2012）：269-275.

［8］ Sebastian T.Understanding the unsteady aerodynamics and near wake of an offshore floating horizontal axis wind turbine［D］.［Ph D Thesis］.University of Massachusetts Amherst，2011.

［9］ Shen Xin，Zhu Xiaocheng，Du Zhaohui.Wind turbine aerodynamics and loads control in wind shear flow［J］.Energy，2011，36（2011）：1424-1434.

［10］Sant T.Improving BEM-based aerodynamic models in wind turbine design codes［D］.［Ph D Thesis］.Delft University of Technology，2007.

［11］Nilay Sezer Uzol，Oguz Uzol.Effect of steady and transient wind shear on the wake structure and performance of a horizontal axis wind turbine rotor［J］.Wind Energy，2011，16（1）：1-17.

［12］Leishman J G，Bagai A，Bhagwat M J.Free-vortex filament methods for the analysis of helicopter rotor wakes［J］.Journal of Aircraft，2002，39（5）：759-775.

［13］Leishman J G.Challenges in modeling the unsteady aerodynamics of wind turbines［J］.Wind Energy，2002，5（2-3）：85-132.

［14］Hand M M，Simms D A，Fingersh L J，et al.Unsteady aerodynamics experiment phase vi：wind tunnel test configurations and available data campaign［R］.Technical report NREL/TP-500-29955，NREL，2001.

［15］Simms D，Schreck S，Hand M，et al.NREL unsteady aerodynamics experiment in the NASA-Ames wind tunnel：a comparison of predictions to measurements［R］.Technical report NREL/TP-500-29494，NREL，2001.

［16］PF，BEP，KSH.The Tjreborg wind turbine loads during normal operation mode for CEC［R］.DG XII.DK.ELSAMPROJEKT A/S，EP94/456.1994.

［17］Yu Guohua，Shen Xin，Zhu Xiaocheng，et al.An insight into the separate flow and stall delay for HAWT［J］.Renewable Energy，2011，36（1）：69-76.

［18］Landgrebe A J.The wake geometry of a hovering rotor and its influence on rotor performance［J］.Journal of the American Helicopter Society，1972，17（4）：2-15.

［19］Massouh F，Dobrev I.Exploration of the vortex wake behind of wind turbine rotor［J］.Journal of Physics：Conference Series，2007，75：012036.

［20］Vatistas G H，Kozel V.A simpler model for concentrated vortices［J］.Experiments in Fluids，1991，11（1）：73-76.

［21］Bagai A，Leishman J G.Rotor free-wake modeling using apseudoimplicit relaxation algorithm［J］.Journal of Aircraft，1995，32（6）：1276-1285.

Aerodynamic characteristics of HAWT rotor in crosswind based on free vortex method

Qiu Yongxing1，Kang Shun1，2
（1.North China Electric Power University，Key Laboratory of CMCPPE Ministry of Education，Beijing 102206，China；2.Xi′an Institute of Modern Control Technology，Xi′an 710065，China）

In order to study the aerodynamic characteristics of HAWT rotor under yawed conditions with shear wind，an unsteady numerical simulation method is developed.It consists of a nonlinear lifting line method and a time-accurate free vortex method.To improve the convergence of the nonlinear lifting line method，an iterative algorithm，based on Newton-Raphson method，is used to solve the circulation equations.In order to improve the accuracy and the efficiency of the algorithm for rotor wake simulation，an improved wake vortex model is developed，which includes a viscous vortex core model，a vortex sheet model and a tip vortex filaments model.The NREL Phase VI and Tjreborg wind turbines are taken as the testing examples.The aerodynamic loads of both the rotor and the blades are computed under different yawed conditions with uniform wind or the shear wind.The results are compared to the experimental data.The key factors and the rules of the aerodynamic characteristics of the rotor and the blades are analyzed.The results show that the method developed in this paper can simulate the aerodynamic characteristics of HAWT effectively under the yawed conditions with shear wind.The fluctuations of shaft torque of blades are increased；the fluctuations of flap moment of blades are decreased at the plus yaw angles and increased at the minus yaw angles.

HAWT rotor；shear wind；yaw wind；unsteady numerical simulation；free vortex method

TK83

：Adoi：10.7638/kqdlxxb-2013.0025

0258-1825（2015）02-0246-08

2013-03-05；

：2013-08-07

国家自然科学基金（51176046）

仇永兴＊（1985-），男，甘肃兰州人，博士研究生，研究方向：风力机空气动力学数值模拟研究.E-mail：qiu＿yx＠163.com

仇永兴，康顺.基于自由涡方法的风轮偏航气动特性研究［J］.空气动力学学报，2015，33（2）：246-253.

10.7638/kqdlxxb-2013.0025 Qiu Y X，Kang S.Aerodynamic characteristics of HAWT rotor in crosswind based on free vortex method［J］.Acta Aerodynamica Sinica，2015，33（2）：246-253.