基于模糊算法的公共自行车服务优化评价系统研究

罗云芳，潘泽锴

(广西职业技术学院 计算机与电子信息工程系，广西 南宁 530226)

0 引言

自行车作为一种节能、环保和健康的交通工具，作为短途出行，是市民选择的最佳交通工具，因此公共自行车服务系统在全国许多城市正在建设普及。公共自行车服务系统主要由管理中心系统，网络通信和站点组成，站点又包括自行车、自行车锁桩和站点控制器。公共自行车服务系统的运营是利用网络通信技术，将站点控制器获取的站点信息数据传送到管理中心系统，管理人员通过管理中心系统实现全城自行车站点的管理。目前城市交通压力大污染越来越严重，作为能减缓城市交通压力和污染速度的交通工具，公共自行车服务系统符合绿色中国行的政策，符合市民的出行需要［1］。

以租赁服务方式提供自行车给市民短途出行，在很多城市已大大方便了市民。但在实际使用中市民常遇到借还车难等情况。站点位置选择，站点锁桩和站点自行车数不合理已影响目前自行车服务系统的运行，因此，对目前系统运行进行优化势在必行［2］。针对大多数城市存在的问题，本文以某城市公共自行车管理中心提供的特定时间段内各个站点借还车数据为研究样本，引入基于模糊算法的控制器，采用模糊数学模型建立优化评价系统，从站点锁桩需求量、自行车数、市民的方便程度和建设费用等因素评价站点选择的合理性。在站点自行车需求量问题上，以站点单位时间内车流量(1 h)为考虑主因，建立线性规划模型得出最优解即所设站点锁桩数量等于可借车数和可停车数之和。同时结合最大锁桩数量的限制，确定出每个站点所需的锁桩数量，运用MATLAB软件将数据进行拟合，进一步优化模型，从而建立公共自行车服务优化评价参数数学模型，为有效的对站点建设评价提供了有力的依据。

1 模糊算法控制器设计

在求解中，常会遇到只能求出模糊解的实际问题。只能求出模糊解的问题用模糊推理逻辑求解更科学合理。模糊推理就是根据已知模糊条件和模糊规则库联合求解可能的模糊结论近似推理的过程［3］。模糊控制器利用模糊理论实现，在处理非线性和没有准确模型等复杂对象时，拥有很好的性能。采用的模糊控制系统结构如图1所示。其中，Ke，Kec与Ku分别为e，ec与u的量化因子［4］。

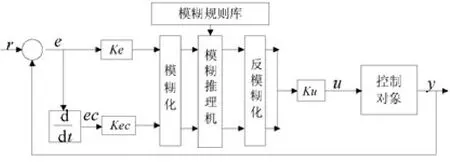
图1 模糊控制系统

模糊控制器由两个输入变量和两个输出变量组成。结合某城市公共自行车管理中心提供的数据特点，在进行模糊控制器的设计之前，使用软件去除原始数据的离异值，通过数据透视统计出各个站点每天的借还车数;统计出各站点累计借车数和还车数，统计出各站点每天用车时长分布情况，在此基础上，锁桩误差e和误差变化率ec为假定的输入变量，即给定的数量与实际需求量进行比较得到误差e和它的微分ec。借还车数为EX1和EX2两个输出变量。输入量经模糊化后转化为用模糊控制语言描述的模糊集合，激活控制规则，经Mamdani模糊推理，离线计算出控制表，最后经过反模糊化得出实际的控制量。模糊控制器由4个步骤设计实现执行:

(1)确定实时的e和ec;

(2)把e和ec的精确量模糊化后的状态E和EC作为控制器的输入;

(3)由模糊规则分别计算控制量EX;

(4)精化模糊控制量EX，将结果u传送到控制单元。

以输入的两个模糊变量作为控制器的输入变量:锁桩的误差E及误差变化率EC。两个输出模糊变量:借车数量EX1，还车数量EX2。在已经对给定数据进行统计处理的基础上，将锁桩误差E及误差变化率EC分为6 档13 级，即{－6，－5，－4，－3，－2，－1，0，1，2，3，4，5，6}，其模糊子集选取如下语言值:{NB(负大)，NM(负中)，NS(负小)，Z(零)，PS(正小)，PM(正中)，PB(正大)};借车数量EX1和还车数量EX2的模糊子集为{G0，G1，G2，G3，G4，G5，G6}，输出变量的量化等级也为 6 档 13 级，即{－6，－5，－4，－3，－2，－1，0，1，2，3，4，5，6}。

在模糊控制理论中，先对变量的量化等级划分，然后确定各变量隶属度函数，每个隶属度函数都拥有不同的含义，模糊子集隶属度函数是模糊集合高分辨率特性的反映，具有较高的控制灵敏度，模糊集隶属度函数是模糊集合低分辨率特性的反映，其特点是系统稳定性好，性能平缓，控制灵敏度较低。为方便计算，采用高斯形隶属度函数表示模糊变量E和EC，输出变量EX1，EX2采用三角形隶属度函数［5］。

2 评价系统建模及优化

利用给定模糊控制系统，并在对变量量化和隶属度函数给定的条件下，采用数据透视结合Excel VBA程序的方法，针对某公共自行车管理中心提供的原始数据，统计出各站点借还车频次和借还车高峰时段，并归类具有共同借还车高峰的站点，计算得出此服务系统在站点位置选择上是否还可以优化。通过模糊算法，对模型进行综合评价，从站点锁桩需求量、自行车数、市民的方便程度和建设费用等因素评价所设站点的合理性。在自行车数量的合理配置上，以各站点单位时间内(1 h)车流量为主要考虑因素［6］，求得模型最优解即所设站点锁桩数量等于可借车数和可停车数之和。

针对公共自行车锁桩数量配置问题，从统计的数据中得出站点1和站点2借还车频次较高。从某城市公共自行车管理中心提供的各站点可借车数和可停车数实时数据可知，站点锁桩数量即可以停放自行车的最大数量，这个值等于站点实时可借车数和实时可停车数之和，站点1和站点2锁桩数量计算结果分别为38个和20个，17:00～17:59这个时段为借车最高峰期，分别借出118和117辆次，而此时段两个站点分别只还回49和95辆次。根据这两个站点的锁桩数量，分析可以得出此时段出现借车频次大于站点锁桩数量和还车频次之和。由此可推断出此时段这两个站点借车是很困难的。为了更好的对当前运行的自行车服务系统锁桩数量配置进行评价，使用如下模型求解。

由于使用公共自行车出行的人数相互独立，而且具有相同的租用概率，因此使用公共自行车出行的人数X的概率服从二项分布X～B(n，r)可得:

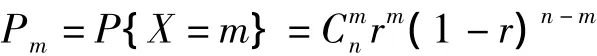
式中P表示租车的概率，随机变量X的期望EX就是X的可能取值与其对应概率乘积的和［7］，形式上EX是X的各种可能取值的加权平均。实际上，EX是X取值的真正“平均”。因此期望值模型是一种平均处理模型，下面是模型Ⅰ:

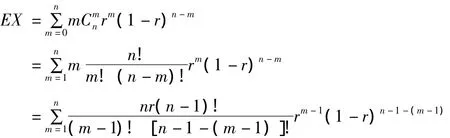
1.自行车站点前一时刻剩余的自行车数大于下一时刻自行车所需数量，是保证想要租用自行车的市民能租到自行车的前提条件:

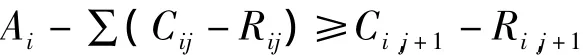
式中Ai表示第i个站点单位时间段内累计的自行车流量，表示第i个站点在j时刻的还车量，Cij表示第i个站点在j时刻的借车量。

2.每个时刻想要还车的人都能在这一服务站点上还车，即有足够的自行车锁桩数:

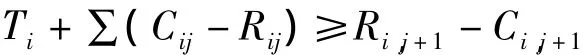
式中Ti表示第i个站点需另设空车位数。

3.服务站点自行车数等于自行车数与空锁桩数之和:

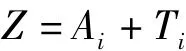
其中

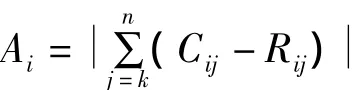
最后将模型优化为:

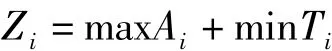
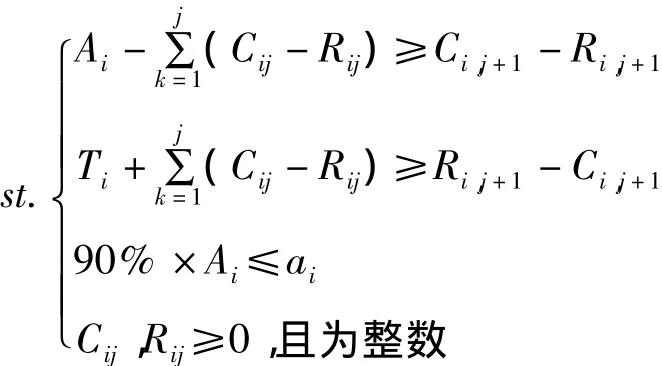
式中Zi表示第i个站点最终确定的自行车数，Ai表示第i个站点最大允许的借还自行车数量。

3 系统仿真

以获取的某自行车公共服务管理中心某个站点一天内自行车借还记录，根据建立的模型Ⅱ，通过曲线拟合的方法，求解算法流程如图2所示。

图2 借还车数求解算法流程

将具体数据代入求解，求得了该站点的自行车借还数量分别为:

利用MATLAB软件对实际借车数量和还车数量进行数据拟合对比，根据对比实际曲线和拟合曲线可以对站点合理性做出判断。

在图3、图4中，曲线1都是实际的借车数或还车数，曲线2为拟合的曲线。对比图3、4中的曲线1和曲线2，借还车实际数量与拟合值相差比较大，因此，目前使用的服务系统站点锁桩数量配置是不合理的，这就要求在设点设锁桩数量时必须满足高峰期对自行车的需求量。

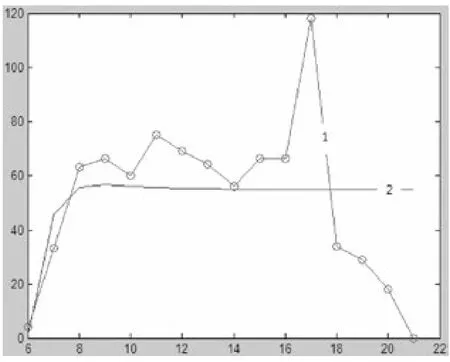
图3 借车数量与拟合曲线图

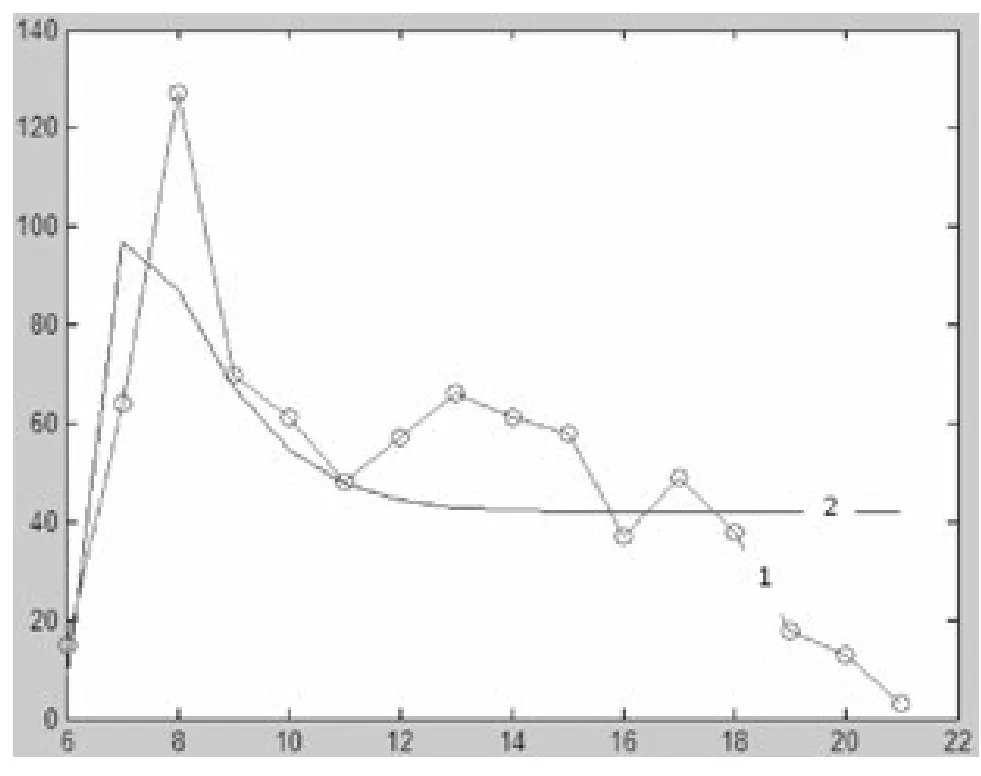
图4 还车数量与拟合曲线图

4 结束语

本文针对现在城市建设中该系统存在的服务站点设置、站点锁桩数量配置不合理的问题，引入了模糊算法控制器，采用模糊数学模型建立优化评价系统进行综合评价，处理数据、分析图形，应用模糊综合评价模型和线性规划模型对服务站点设立和自行车数量配备进行合理性评价，最后使用软件选取其中的任意一个站点进行仿真表明，该系统能够有效的评判站点的合理性。

［1］刘引涛，刘楠.公共自行车服务系统站点及锁桩设置评价模型的分析研究［J］.电子设计工程，2014，22(23):11－13.

［2］贾俊平，何晓群，金勇进.统计学［M］.北京:中国人民大学出版社，2004.

［3］党小超，张春娇，郝占军.基于模糊元胞自动机的网络舆情传播模型研究［J］.计算机工程，2014，40(4):209－213.

［4］张立东，贾磊，朱文兴.基于模糊理论的交通溢流识别算法［J］.计算机应用，2012，32(8):2378－2384.

［5］樊春丽，朱名日.蔗糖结晶过程的建模与控制［J］.计算机系统应用，2009(3):38－41.

［6］姜启源.数学模型(第三版)［M］.北京:高等教育出版社，2003.

［7］薛薇.SPSS统计分析方法及应用［M］.北京:电子工业出版社，2013.