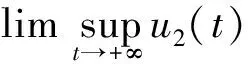时标上具有反馈控制的两种群竞争系统的持久性分析
(1.玉溪市教育局;2.玉溪市第四中学,云南 玉溪 653100)
自20世纪以来,生态问题越来越受到人们的普遍关注,而以常微分方程为理论基础的数学生态学已经形成了比较完善的体系,对整个生物学领域产生了重要的影响.在生态数学中,种群生态学是人们最感兴趣的分支之一.自然界中任何一种物种都不是孤立存在的,它必然与其他物种有各种关系,而在这些关系中最常见的则为物种竞争的关系.人们只有了解种群的演变规律和掌握了种群之间的相互关系,才能够合理的控制和改善生态系统,对生态系统进行合理的保护、开发和利用.
1 模型简介
文献[1]研究了如下连续系统
(1)
其中,x1,x2,u1,u2分别表示关于时间t的种群密度和关于时间t的反馈控制变量(详细生物背景见文献[1]及其参考文献).
应用微分方程比较原理及不等式技巧,文献[1]得到了系统(1)概周期解存在的充分条件.文献[2,3]等文献则研究了离散时的系统的持久性及其概周期解的存在性.而众所周知,在自然界中,种群的存在和分布并不都是理想中的连续分布,许多情形是既有连续又存在离散.1988年,德国数学家Stefan Hilger整合统一了连续分析和离散分析,发现了微积分算法和差分演算法之间的深层关系,最终提出了时间尺度(Time Scales)上的分析理论[4].文献[5~7]均在时间尺度上对种群生态系统的持久性等动力学行为进行了研究.受以上文献思想的启发,笔者对如下两种群竞争系统进行讨论:

(2)
(3)
因此,本文的主要目的是讨论时间尺度上带有反馈控制两种群竞争系统的持久性问题,即系统(2)的持久性.
在本文中,我们假设如下条件成立:
(H1)ri(t),ai(t),bi(t),ci(t),di(t),hi(t),ei(t),fi(t)(i=1,2)是定义在时间尺度上的右连续有界实值函数且使得如下成立:



2 预备知识
在这一部分,先介绍本文用到的一些基本定义和引理.这些概念的定义以及引理的证明可以参见文献[4].
σ(t)=inf{s∈∶s>t},ρ(t)=sup{s∈∶s 一个点t∈称作是左稠密的,如果t>inf且ρ(t)=t;称作是左分散的,如果ρ(t) 一个函数f∶⟹R称作是右稠密连续的,如果它在中的右稠密点是连续的,且在中的左稠密点的左极限是存在的.如果f在每一个右稠密点与左稠密点均是连续的,则称f是上的连续函数.我们定义C[J,R]={u(t)∶u(t)是J上连续的},以及C1[J,R]={u(t)∶u△(t)是J上连续的}. 对于y∶t→R,其中t∈k,我们定义y(t)的delta导数y△(t)是这样一个(如果它存在)具有如下性质的数:对于给定的ε>0,存在t的一个邻域U使得 |[y(σ(t))-y(s)]-y△[σ(t)-s]|<ε|σ(t)-s| 对于所有的s∈U都成立. 如果y是连续的,那么y是右稠密连续的,如果y在t是delta可微的,那么y在t是连续的. 如果y是右稠密连续的,令Y△(t)=y(t),则我们定义delta积分如下: 定义1 系统(2)是持久的,如果对系统(2)的任意解(x1(t),x2(t),u1(t),u2(t))T,存在正常数mi,qi,Mi和Qi(i=1,2)使得如下成立 引理1[7]设-a∈R+. 命题1 假设条件(H1)-(H3)成立.则系统(2)的所有解(x1(t),x2(t),u1(t),u2(t))T满足 其中 证明设(x1(t),x2(t),u1(t),u2(t))T是系统(2)的任意正解,则由系统(2)的第一个方程和Bernoulli不等式exp{x}≥1+x,对任意的x∈,可得 (4) 应用引理1的结果,(4)式可得 (5) (6) 应用引理1,(6)式可得 (7) 设ε→0,应用类似的讨论方法,系统(2)的第四个方程可得 (8) 应用引理1,(8)式可得 (9) 同理,由系统(2)的第二个方程和(9)式, ≤r2(t)-b2(t)(x2(t)+1)+d2(t)eu2*+ε (10) 应用引理1,(9)式可得 当ε→0,(7)式和(9)式可得 (11) (12) 证毕. 命题2 设条件(H1),(H4)-(H5)成立.则系统(2)的所有解(x1(t),x2(t),u1(t),u2(t))Τ满足 证明设(x1(t),x2(t),u1(t),u2(t))Τ是系统(2)的任意正解,我们首先证明 对任意小的常数ε≥0,存在一个点Τ1∈且Τ1≥Τ0使得如下不等式成立 (13) 由系统(2)的第一个方程和条件(H),当t>Τ1时, 我们断定 (14) 则可得 (15) 当ε→0时,可得 (16) 从而,对任意小的ε>0,存在一个点Τ2∈使得x1(t)≥x1*-ε,t≥Τ2.于是,由系统(2)的第二个方程可得 应用类似(16)的方法,可得 (17) (18) 应用引理1,可得 (19) 类似以上证明方法,不难得出 也即 (20) 当ε→0时,可得 (21) (22) 故性质2证毕. 定理1 若条件(H1)-(H5)成立,则系统(2)是持久的.记集合Ω是系统(2)的所有解(x1(t),x2(t),u1(t),u2(t))Τ且满足 ∀t∈.事实上,由命题1和2的证明结果可知,定理1是成立的并且Ω是系统(2)的一个不变集. [1]Z.Liu,Persistence and periodic solution in two species competitive system with feedback controls[J].Biomath,2002(17):251-255. [2]X.Liao,Z.Ouyang,and S.Zhou,Permanence of species in non-autonomous discrete Lotka-Volterra competitive system with delays and feedback controls[J]. Journal of Computational and Applied Mathematics,2008,211(1):1-10. [3]T.Zhang,Y.Li,and Y.Ye,Persistence and almost periodic solutions for a discrete fishing model with feedback control[J]. Communications in Nonlinear Science and Numerical Simulation,2011,16(3):1564-1573. [4]M.Bohner and A.Peterson,Advances in Dynamic Equations on Time Scales[M].Birkh user,Boston,Mass,USA,2003. [5]Y.K.Li,X.F.Han,Almost periodic solution for aN-species competition model with feedback controls on time scales[J].Journal of Applied Mathematics & Informatics,2013,31(1-2),247-262. [6]Y.H.Zhi,Z.L.Ding,Y.K.Li,Permanence and Almost Periodic Solution for an Enterprise Cluster Model Based on Ecology Theory with Feedback Controls on Time Scales[J].Discrete Dynamics in Nature and Society,Vol.2013,Article ID:639138:14. [7]H.T.Zhang,F.D.Zhang,Permanence of anN-species cooperation system with time delays and feedback controls on time scales[J].Journal of Applied Mathematics and Computing,2014,46(1-2):17-31.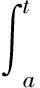




3 持久性