(2+1)维非线性偏微分方程的精确解

(西安培华学院 基础部,陕西 西安 710125)

随着现代数学和物理学的发展,非线性偏微分方程的求解问题特别是对一些高维的非线性微分方程的求解成为研究的热点.近年来,对非线性偏微分方程寻找对称约化和构造精确解方面的研究取得了很大的进展.为了得到非线性偏微分方程的精确解,研究者提出了很多方法来解决,诸如经典的李群方法[1]、非经典的李群方法[2]、CK直接法[3]和改进的CK直接法[4].本文研究(2+1)维Calogero-Bogoyavlenskii-Schiff(CBS)方程

4uxt+uxxxz+4uxuxz+2uxxuz=0

(1)

文献[5]利用Hirota双线性法求出了CBS方程的部分多孤子解;文献[6]利用经典的李对称方法给出了CBS方程的李点对称;文献[7]给出了(2+1)维广义CBS方程的无穷多对称及其约化;文献[8]利用李群分析法和行波约化法给出了(2+1)维CBS方程的相似解;文献[9]利用拓展的双曲函数展开法求出了该方程的行波解.本文利用非古典对称方法得到(2+1)维CBS方程的群不变解,然后将该方程约化为常微分方程,最后得到了该方程一些新的精确解.

1 (2+1)维CBS方程的对称

非线性发展方程

Φ(x,z,t,ux,ut…)=0

(2)

称函数σ(x,z,t,ux…)为方程(2)的一个对称，如果

Φ'(u)σ=0

(3)

对于任意的u都成立.其中

对于(2+1)维CBS方程(1),利用(2)可得到方程(1)的对称满足的方程如下:

σxxxz+4σxt+4σxuxz+4σxzux+2σxxuz+2uxxσz=0.

(4)

下面利用待定系数法[10，11]求解方程(1)的σ.假设方程(1)有如下形式的解

σ=a(x,z,t)ut+b(x,z,t)ux+c(x,z,t)uz+d(x,z,t)u+e(x,z,t)

(5)

其中a,b,c,d,e为待定函数.将方程(5)代入方程(1),并且利用-4uxt-4uxuxz-2uxxuz替换uxxxz,即可得到关于a,b,c,d,e的偏微分方程组

ax=0,az=0,bz=0,cx=0,dz=0,dxx=0,d-bx=0,4dx+bxx=0,2bt+ez=0

4ext+exxxz=0,3dxx+4ct+bxxx+4ex=0,dt+bxt+exz=0,at-2bx-cz=0

通过求解该决定方程组可得

a=2f1t2+(2f2+f3)t+f4,b=(f1t+f2)x+φ(t),d=f1t+f2c=(2f1z+f5)t+f3z+f6,e=-x(2f1z+f5)-2zφ'(t)+ψ(t)

(6)

其中φ(t),ψ(t)为t的任意函数,fi(i=1,2,3,4,5,6)为常数.则方程(1)的对称为

σ=[2f1t2+(2f2+f3)t+f4]ut+[(f1t+f2)x+φ(t)]ux+[(2f1z+f5)t+f3z+f6]uz+

[f1t+f2]u+[-x(2f1z+f5)-2zφ'(t)+ψ(t)].

(7)

2 (2+1)维CBS方程的群不变解

为得到方程(1)的对称约化,利用σ=0和方程(1)的相容性,先求解σ=0时方程(1)的特征方程组

(8)

现在讨论以下几种情况:

情况(1):令f1=f4=φ(t)=f5=f6=ψ(t)=0,f2=f3=1

特征方程为

解特征方程可得到它的不变解为

(9)

将(9)式代入方程(1).就可以将方程(1)约化为下面的方程

6hθθhω-8hθ-4θhθθ-4ωhθω+12hθhθω+3hθθθω=0.

(10)

情况(2):令f1=f2=f3=f4=f5=ψ(t)=0,f6=-a

其特征方程为

解特征方程可得到它的不变解为

(11)

将(11)代入方程(1)得到约化方程为

(12)

情况(3):令f1=f4=f6=φ(t)=ψ(t)=0,f3=-2,f2=f5=1

其特征方程为

解特征方程可得到它的不变解为

(13)

将(13)代入方程(1)得到约化方程为

(14)

情况(4):令f1=f4=f5=f6=ψ(t)=0,f2=f3=1,φ(t)=t

其特征方程为

解特征方程可得到它的不变解为

(15)

将(15)代入方程(1)得到约化方程为

6ω2hθθθω-6ωhθθθ+6ωhθhθω-2θω2hθθ+3ωhθθhω-3hhθθ-2ω3hθω-2ω2hθ=0

(16)

情况(5):令f1=f2=f3=f6=ψ(t)=0,f4=f5=φ(t)=1

其特征方程为

解特征方程可得到它的不变解为

(17)

将(17)代入方程(1)得到约化方程为

hθθθω+4θhθω-4hθhθω+2hω-2hωhθθ-4hθθ=0

(18)

3 (2+1)维CBS方程的精确解

通过解约化方程(12)就可得到方程(2+1)维CBS方程的一些新的精确解,然后作下面的变换

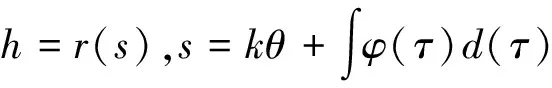
(19)

方程(12)就可约化为常系数常微分方程

(20)

(21)

即方程(1)就可约化为方程(20).对方程(20)两边同时积分后在同时乘以h''在积分,然后令h'=g得

(22)

求解上式方程的解就可以得到方程(1)的一些新的精确解:

a)如果b=c=0,ak<0方程(22)的解如下

(23)

(24)

因此方程(20)的解为

(25)

(26)

由方程(21)、(25)、(26)可得方程(1)的新精确解为

(27)

(28)

b)如果b=c=0,ak>0方程(1)的解为

(29)

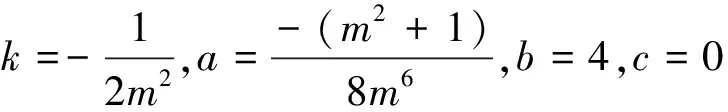
则方程方程(1)的解为

(30)

则方程(1)的解为

(31)

则方程(1)的解为

(32)

4 结 论

本文通过李群分析法得到(2+1)维CBS方程的对称，然后利用特征方程得到群不变解将该方程约化为常微分方程，并求得该方程一些新的精确解，其中包括雅克比椭圆函数解、三角函数解.这些解在数学物理中有着重要的应用,这种方法也可以适用于其他高维的非线性微分方程的求解.

[1]OLVER P J.Application of lie group to differential equations[M].Berlin:Springer,1986.

[2]楼森岳，唐晓燕.非线性数学物理方法[M].北京:科学出版社,2006.

[3]CLARKSON P A.KRUSKAL M D.New similarity reductions of the boussinesq equation[J].J Math Phys,1989,30:2201-2212.

[4]LOU S Y,MA H C.Non-Lie symmetry groups of (2+1)-dimensional nonlinear systems obtained from a simple direct method[J].J Phy A:Math Gen,2005(38):129-137.

[5]WAZWAZ Abdul-Majid.Multiple-soliton solutions for the Calogero-Bogoyavlenskii-Schiff,Jimbo-Miwa and YTSF equation[J].Appl Math Comput,2008,203(2):592-597.

[6]智红燕.(2+1)维Calogero-Bogoyavlenskii-Schiff方程的对称约化及其新的类孤子解[J].中国石油大学学报:自然科学版,2010,34(3):170-173.

[7]ZHANG H P，CHE Y,LI B.(2+1)维广义Calogero-Bogoyavlenskii-Schiff方程无穷多对称及其约化[J].物理学报,2009,58(11):7393-7396.

[8]M.L.Gandarias1,M.S. Bruzon1,Symmetry group analysis and similarity solutions of the CBS equation in (2+1) dimensions[J].Appl. Math. Mech,2008,8:10591-10592.

[9]Wazwaz A.M. New solutions of distinct physical structures to high-dimensional nonlinear evolution equations[J].Applied Mathematics and Computation,2008,196:363-370.

[10]李富志,刘希强.Jimbo-Miwa方程的对称约化及不变解[J].量子电子学报，2008,25(2):155-160.

[11]刘娜,刘希强.(2+1)维Boiti-Leon-Manna-Pempinelli方程的对称，精确解及守恒律[J].量子电子学报，2008,25(5):546-552.