考虑锚固复合承载体效应的巷道安全支护参数分析

王 超 赵光明 孟祥瑞

(1.煤矿安全高效开采省部共建教育部重点实验室，安徽 淮南232001;2.安徽理工大学能源与安全学院，安徽 淮南232001)

巷道支护力与变形量是影响巷道稳定性的重要因素，而实际的支护力一般仅为原岩应力的1/100 ～1/10［1-3］，为分析实际支护力对巷道围岩的有效支护问题，在理想弹塑性条件下一些学者通过芬纳－卡斯特奈公式初步推导出了圆形巷道最小支护力和最大允许变形量计算公式［4］，在考虑巷道塑性区内聚力与松动压力的条件下对计算结果进行了修正［5］。基于巷道围岩应力大小和力学状态分布规律，文献［6-10］将巷道围岩划分为内、外承载结构，推导了外承载结构有关特征参数的表达式，揭示了外承载结构特征参数与巷道围岩稳定性的关系，以及内承载结构支护强度与外承载结构特征参数的关系。文献［11］提出了锚固复合承载体的概念，推导出了锚固复合承载体强度的计算方法。以上理论是把支护力简化为一个分布在巷道表面的均布力，未计算锚杆支护形成的承载结构对巷道最小支护力与最大允许变形量的影响。

在前人研究的基础上，本研究以锚固复合承载体为结构基础，依据岩石的极限拉压破坏准则并结合芬纳－卡斯特奈公式，对圆形巷道支护力和变形量进行分析。

1 锚固复合承载体力学模型

在静水压力状态下的水平圆形巷道，忽略巷道影响范围内岩石自重，基于锚固复合承载体处于巷道塑性区内的认识，建立如图1 所示的锚固复合承载体力学模型。其中，p0为原岩应力，pi为锚杆支护强度，b为锚固复合承载体厚度，巷道半径为r。Fn为巷道横截面上受到的垂直载荷，以巷道轴线为轴对称分布，该部分载荷沿巷道两帮由外到内分布，可描述为Fn= pc+f( x) ;pc为锚固复合承载体在巷道表面的切向应力，f(x)为垂直应力沿径向增量分布函数，并假设f(x)为斜率等于k' 的线性函数，则f(x)=k'x。

图1 锚固复合承载体力学模型Fig.1 Mechanical model of composite bolt-rock bearing structure

在极限平衡状态下，根据莫尔－库仑准则并结合锚固复合承载体在垂直方向上的静力平衡方程，按照文献［10］最终得出锚固复合承载体的强度为

令

则

其中，φ' 和c' 分别为锚固复合承载体的内摩擦角和内聚力。

2 巷道最小支护力和最大允许变形量

2.1 围岩塑性破坏条件

在单轴压缩试验条件下，岩石的轴向线应变达到一定值ε0时岩石就会破坏。根据岩石在真三轴试验条件下岩石的变形特征，在低围压条件下，岩石的变形能力随着围压σ3的增加可近似为线性增加［12］。在支护力的作用下，巷道开挖后周边各点呈三向应力状态［13］，比原岩应力小得多，巷道表面围岩处于低围压状态。假设围岩为理想弹塑性材料，且岩体的变形性能与岩石类似，由此得到低围压状态下岩体的最大主应变εm与围压σ3的关系为

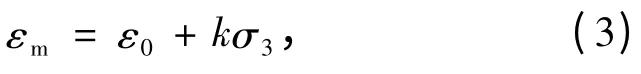
其中，ε0为单轴压缩线应变的极限值;k 为低围压下岩体变形能力增长率。将式(3)作为研究围岩塑性破坏的条件。施加支护力时，支护力pi= σ3，代入公式(3)得岩体的最大主应变εm与支护力pi的关系为

2.2 不考虑锚固复合承载体效应分析

在支护力pi的作用下，根据芬纳－卡斯特奈公式［14-15］，求得塑性区各点的径向位移为

式中，φ 为岩体内摩擦角，μ 为岩体泊松比，c 为岩体内聚力，E 为岩体弹性模量，ρ 为塑性区各点的极半径。根据公式(5)可知，在巷道表面处的径向位移量最大，取ρ = r，并根据对称性求得塑性区切向线应变为

根据图2 可知，随着pi的增加，εθ，r逐渐变小、εm呈线性增加，当两者相等时支护力pi取得极限最小值pmin，即

图2 最小支护力示意Fig.2 Sketch map of minimum supporting force

将式(4)、式(6)代入式(7)得

当pi取得极限最小值pmin时，对应u 所取得的围岩最大允许变形量umax为

围岩最小支护力和最大允许变形量与围岩性质和支护力密切相关，式(9)和式(10)是假设支护力pi均匀分布在巷道表面上得出的，未计算由于锚固作用形成的复合承载体对于围岩支护关系的影响。

2.3 考虑锚固复合承载体效应分析

根据假设，锚固复合承载体处于巷道塑性区内，在极限平衡状态下，锚固复合承载体外部围岩的最小支护阻力即为锚固复合承载体的强度，由此得出锚固复合承载体外部围岩最大允许变形量为

将式(2)代入式(11)得出锚固复合承载体外部围岩最小支护力表达式为

式中，

3 算例分析

某水平圆形巷道，侧压系数λ =1，巷道半径r =2.5 m，地层平均容重γ =25 kN/m3，H 为巷道埋深，原岩应力p0= γH，承载体外岩体弹性模量E =3.47 GPa，岩体内聚力c =1 MPa，岩体单轴压缩线应变的极限值ε0=3 ×10－3，承载体的内聚力c' =0.8 MPa，低围压下岩体变形能力增长率k =1 ×10－3/MPa，取岩体内摩擦角φ =30°。

由式(9)得出不考虑锚固复合承载体效应时巷道最小支护力为

式中，

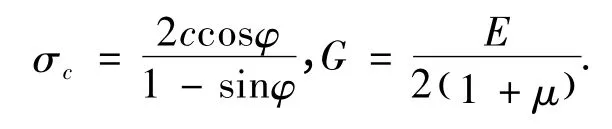
由式(10)得出不考虑锚固复合承载体效应时巷道最大允许变形量为

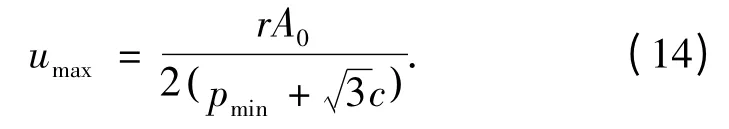
由式(11)得出考虑锚固复合承载体效应时巷道最大允许变形量为

由式(12)得出考虑锚固复合承载体效应时巷道最小支护力为

式中，

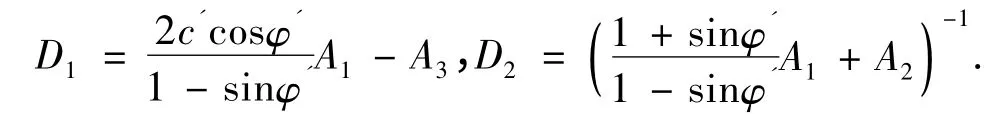
3.1 锚固复合承载体厚度比n 对、影响

取锚固复合承载体内摩擦角φ' =30°，通过单因素控制法，令n = b/r，讨论锚固复合承载体厚度对和的影响，如图3 和图4 所示。

图3 锚固复合承载体厚度比n 对的影响Fig.3 The impact of the thickness n of composite bolt-rock bearing structure on

图4 锚固复合承载体厚度比n 对的影响Fig.4 The impact of the thickness n of composite bolt-rock bearing structure on

由图3 可以看出，锚固复合承载体厚度一定时，随着巷道埋深的增加，最小支护力呈线性增加;在巷道埋深一定，锚固复合承载体厚度增加时，最小支护力随之减小;在n ＞1 时，最小支护力基本维持在1 MPa 以下。

由图4 得出，锚固复合承载体厚度一定时，随着巷道埋深的增加，巷道最大允许变形量呈线性增加;在巷道埋深一定，锚固复合承载体厚度逐渐增加时，最大允许变形量随之增加。

3.2 锚固复合承载体内摩擦角φ'对、的影响分析

锚固复合承载体厚度b 取1.5 m，同样采用单因素控制法，讨论锚固复合承载体内摩擦角φ'对和的影响，如图5 和图6 所示。

图5 锚固复合承载体内摩擦角φ'对的影响Fig.5 The impact of the internal friction angle φ'of composite bolt-rock bearing structure on

图6 锚固复合承载体内摩擦角φ'对的影响Fig.6 The impact of the internal friction angle φ'of composite bolt-rock bearing structure on

由图5 可知，锚固复合承载体内摩擦角φ' 一定时随着巷道埋深的增加，最小支护力呈线性增加; 锚固复合承载体内摩擦角 φ' 变大时，最小支护力随之减小; 当 φ'大于 35°时，最小支护力基本不超过 1MPa。

由图6 得出，随着巷道埋深的增加，锚固复合承载体内摩擦角φ' 一定时，巷道最大允许变形量随之增加;在巷道埋深一定，锚固复合承载体内摩擦角逐渐增加时，最大允许变形量随之增加。

3.3 锚固复合承载体与不考虑锚固复合承载体的对比分析

巷道埋深H 大于300 m，取上述锚固复合承载体厚度比n 与内摩擦角φ' 的最大与最小值，与不考虑锚固复合承载体的结果进行对比分析，讨论考虑锚固复合承载体计算结果的合理性，如图7 和图8 所示。

图7 最小支护力对比Fig.7 The comparison of minimum supporting force

图8 最大允许变形量对比Fig.8 The comparison of the maximum allowable deformation

由图7 可得，巷道埋深不足350 m 时，巷道最小支护力接近于0，pmin小于1.0 MPa;巷道埋深在350 ～650 m 时，巷道最小支护力基本在0 到1 MPa 之间，pmin最大超过了2.5 MPa;巷道埋深超过650 m 时，巷道最小支护力在1 ～2 MPa 之间，pmin最大超过了3.5 MPa。说明巷道埋深较浅时，巷道在较小的支护力下就能保持稳定;当巷道埋深大于350 m 时，巷道最小支护力pmin要比1 MPa 大得多，而实际的支护力一般为原岩应力的1/100 ～1/10，显然此时考虑锚固复合承载体计算结果更合理。

由图8 可知，巷道最大允许变形量umax最大不超过20 mm，随着巷道埋深的增加umax变化非常小，巷道埋深每增加100 m，umax增加不超过2 mm，与实际相差较大;都在20 mm 以上，随着巷道埋深的增加变化较明显，其允许变形量与实际巷道产生的变形量较为吻合。

4 结 论

(1)针对以往研究未计算锚固复合承载体对巷道最小支护力与最大允许变形量的影响问题，以锚固复合承载体为结构基础，从巷道塑性破坏条件出发，推导出圆形锚杆支护巷道最小支护力和最大允许变形量的表达式。

(3)通过对比分析，在锚杆支护的巷道中考虑锚固复合承载体计算圆形巷道支护力和变形量结果更合理，与实际较为吻合。说明了锚固复合承载体存在的重要意义，同时也证明了文中推导结果的合理性，解释了在较小的支护力下能够实现巷道长期稳定的原因。研究成果对实际巷道安全支护工程有一定帮助，但未能进行更加全面的分析，在未来的研究中，还需深入研究各种影响巷道稳定的支护参数，以期为特定巷道的支护系统建立系统性安全评价机制奠定理论基础。

［1］ 杨 超，陆士良，姜耀东. 支护阻力对不同岩性围岩变形的控制作用［J］. 中国矿业大学学报，2000，29(2):170-173.

Yang Chao，Lu Shiliang，Jiang Yaodong. Controlling effects of support resistance on roadway deformation under different rock conditions［J］. Journal of China University of Mining ＆ Technology，2000，29(2):170-173.

［2］ 许 广，唐又驰. 深部软岩煤巷围岩变形分析与控制技术研究［J］. 中国安全科学学报，2011，21(2):109-114.

Xu Guang，Tang Youchi. Research on deformation and control of coal tunnel in deep soft rock［J］. China Safety Science Journal，2011，21(2):109-114.

［3］ 王同旭，麻洪蕊. 巷道支护力作用及影响因素分析［J］. 山东科技大学学报:自然科学版，2009，28(4):40-42.

Wang Tongxu，Ma Hongrui. The effect of roadway supporting forces and analysis of its influence factors［J］. Journal of Shandong University of Science and Technology :Natural Science，2009，28(4):40-42.

［4］ 汤伯森. 弹塑围岩最小支护抗力和最大允许变形的估算［J］.岩土工程学报，1986，8(4):81-88.

Tang Bosen. Estimation of elastic-plastic surrounding rock the minimum support resistance and the maximum allowable deformation［J］. Chinese Journal of Geotechnical Engineering，1986，8(4):81-88.

［5］ 杨清廷. 圆形洞室最小支护抗力和最大允许变形探讨［J］. 成都科技大学学报，1989，48(6):48-52.

Yang Qingting. Study on the minimum support resistance and maximum allowable deformation of the circular tunnel［J］. Journal of Chengdu University of Science and Technology，1989，48(6):48-52.

［6］ 孔 恒，王梦恕，高海宏. 岩体锚固承载结构的构成分析［J］.西部探矿工程，2003，81(2):97-99.

Kong Heng，Wang Mengshu，Gao Haihong. Analyses of supporting structure of rock bolting［J］. West-China Exploration Engineering，2003，81(2):97-99.

［7］ 李树清. 深部煤巷围岩控制内、外承载结构耦合稳定原理的研究［D］. 长沙:中南大学，2008.

Li Shuqing. Study on Principal of Inner-outer Bearing Structures Coupling Stabilization for Strata Control Around Deep Coal Drifts［D］. Changsha:Central South University，2008.

［8］ 李树清，王卫军，潘长良. 深部巷道围岩承载结构的数值分析［J］. 岩土工程学报，2006，28(3):377-381.

Li Shuqing，Wang Weijun，Pan Changliang. Numerical analysis on support structure of rock around deep roadway［J］. Chinese Journal of Geotechnical Engineering，2006，28(3):377-381.

［9］ 康红普. 巷道围岩的关键圈理论［J］. 力学与实践，1997，19(1):34-36.

Kang Hongpu. Key zone theory of roadway surrounding rock［J］. Mechanics and Practice，1997，19(1):34-36.

［10］ 朱建明，徐秉业，任天贵，等. 巷道围岩主次承载区协调作用［J］. 中国矿业，2000，9(2):41-44.

Zhu Jianming，Xu Bingye，Ren Tiangui，et al. Coordination between primary and secondary support zones of drift's surrounding rock［J］. China Mining Magazine，2000，9(2):41-44.

［11］ 张益东. 锚固复合承载体承载特性研究及在巷道锚杆支护设计中的应用［D］. 北京:中国矿业大学，2013.

Zhang Yidong. Study on Bearing Characteristic of Composite Bolt-Rock Bearig Structure and Its Application in Roadway bolting Design［D］. Beijing:China University of Mining ＆ Technology，2013.

［12］ 沈明荣，陈建峰. 岩体力学［M］. 上海:同济大学出版社，2006:27.

Shen Mingrong，Chen Jianfeng. Rock Mechanics［M］. Shanghai:Tongji University Press，2006:27.

［13］ 刘泉声，张 华. 对煤矿深部岩巷围岩稳定与支护几个关键问题的认识［J］. 岩石力学与工程报，2003，22(S1):2195-2200.

Liu Quansheng，Zhang Hua. Study on stability and support of rock masses surrounding deep coal-mine roadway［J］. Chinese Journal of Rock Mechanics and Engineering，2003，22(S1):2195-2200.

［14］ Kastner H. 隧道与坑道静力学［M］. 同济大学隧道与坑道静力学翻译组，译. 上海:上海科学技术出版社，1980:46-56.

Kastner H. Tunnel and Tunnel Statics［M］. Translated by Tongji University Tunnel and Tunnel Statics Translation Group. Shanghai:Shanghai Science and Technology Publishing House，1980:46-56.

［15］ 蔡美峰. 岩石力学与工程［M］. 北京:科学出版社，2006.

Cai Meifeng. Rock Mechanics and Engineering［M］. Beijing:Science Press，2006.