某方解石矿群空区稳定性数值模拟分析

王 星 吴学文 孙国权

(1.中钢集团马鞍山矿山研究院有限公司，安徽 马鞍山243000;2.金属矿山安全与健康国家重点实验室，安徽 马鞍山243000;3.华唯金属矿产资源高效循环利用国家工程研究中心有限公司，安徽 马鞍山243000;4 青阳县兴达矿业有限责任公司，安徽 青阳242802)

1 概 况

青阳县某方解石矿山自2002 年开始建矿开采以来，在井下已经形成了大面积的采空区，成为矿山安全生产的重大安全隐患，为了保证矿山下一步的安全生产和周围居民的安全，有效预防采矿引起的地质灾害和矿山安全生产事故，需根据矿山实际情况对现有采空区进行精确测量及稳定性判别，以便后续制定合理的治理措施，消除采空区的安全隐患。

1.1 矿床水文地质

1.2 矿床工程地质

本矿床岩石以中厚层大理岩、白云石大理岩为主，属层状结构，岩石坚硬完整质量良好。因此，矿体及围岩稳定性好。局部因断裂构造和节理裂隙密集，岩石切割强烈，由黏土充填，坑道需支护，但对坑道掘进不致造成严重困难。矿床工程地质条件简单，区域地震烈度Ⅵ度区，本区地震烈度为Ⅵ度区。地震分组第一组，设计地震加速度0.05g，场地类型I 类型，特征周期0.25 s。岩石以层状结构为主，力学强度高，岩石坚硬，岩体质量良好。

2 采空区调查

矿山采用平硐开拓，已经形成+184 m、+220 m、+242 m、+267 m 4 个中段。采矿方法设计采用浅孔落矿的平底空场法，采场宽15 ～20 m，局部达30 m，采高4 ～18 m 不等，局部达25 m。采场之间留不规则矿柱，一般宽5 ～10 m。经过多年的开采，该矿山已在4 个中段分别形成一定规模不规则的采空区和矿柱。采空区统计见表1。

表1 采空区基本信息Table 1 Basic information of goaf

+190 m 中段的采空区投影面积为20 167.45 m2，采空区内主要矿柱为点柱，矿柱投影面积为3 370.3 m2，矿柱和采空区投影面积比为0.167。+220 m 中段的采空区投影面积为18 364.59 m2，采空区内主要矿柱为点柱，矿柱投影面积为7 015.5 m2，矿柱和采空区投影面积比为0.382。+245 m 中段的采空区投影面积为13 993.8 m2，采空区内主要矿柱为点柱，矿柱投影面积为5 455.8 m2，矿柱和采空区投影面积比为0.389。+267 m 中段的采空区投影面积为15 574.1 m2，采空区内主要矿柱为点柱，矿柱投影面积为1 354.4 m2，矿柱和采空区投影面积比为0.087。

3 群空区稳定性数值模拟分析

此次数值模拟以本矿山的采空区为对象，建立有限差分网格模型，按照采空区基本信息进行按走向每隔15 m 留设5 m×5 m 矿柱条件下形成采空区和分次增大采空区顶板暴露面积情况下模型的数值模拟。通过模拟计算，分析以下内容:①不同间隔矿柱支撑下的采空区稳定性，主要包括不同组合类型矿柱支撑下，采空区的顶柱、上下盘围岩内的应力、应变情况;②采空区在现有矿柱支撑情况下是否稳定，并研究采空区对上部开采区域的影响程度。

3.1 三维数值计算模型

本次计算结合矿山的水文地质条件、工程地质条件、矿体赋存条件及所用采矿方法的特点，建立模型，从采空区围岩受采动影响、矿柱承载能力变化、采空区顶板应力及位移状态和地表变形等方面进行采空区稳定性的数值模拟，最终确定的模型如下:长度320 m，宽度200 m，高度320 m，模型共有179 200 个单元，189 215个节点。

(1)岩体力学参数。根据矿山的工程地质特征，进行了岩体物理力学参数折减，本次数值模拟过程中所用岩体力学参数见表2。

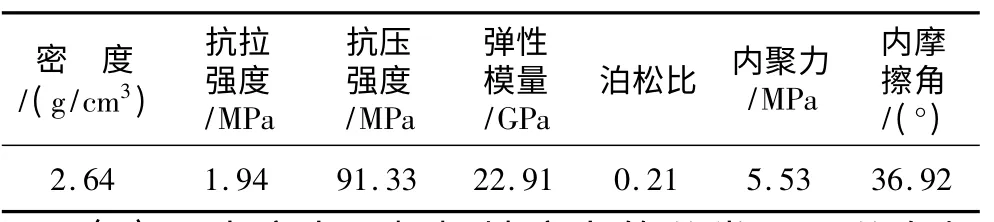
表2 小晶体方解石岩体力学参数Table 2 Mechanical parameters of small crystal calcite rock mass

(2)原岩应力。根据地应力的分类以及分布规律结合该矿区的地质情况和工程地质调查，开采区域出露地表，没有较大的构造应力，而且空区埋藏较浅，因此模型的初始应力场仅考虑自重应力。

(3)模型边界条件。由于计算模型的尺寸已经考虑了采空区形成以后的影响范围，因此只需要在模型前后、左右及底面施加约束即可，其中对模型前后及左右方向均施加水平方向约束，在模型底部施加垂直方向的约束，模型顶面为自由面。

当P1既定时，地方政府采取机会主义和不采取机会主义的预期收益是相等的。若令T为地方政府获得的实际收益额，S为地方政府采取机会主义行为的成本，那么，地方政府机会主义的净收益T-S越高，上级政府实施监督的概率就大。再令上级政府对其处以净收益r倍的经济处罚，即r（T-S），处以a的非经济处罚，效应为-F（a），则上级政府对地方政府实施处罚的程度r（T-S）越大，F（a）越大，上级政府监督的概率就越小。

3.2 模拟方案

数值计算按以下步骤进行。

(1)形成初始应力场。根据3.1 节建立的模型，按照主应力与垂直深度的变化关系形成初始应力场，使模型达到初始应力平衡状态。

(2)构建采空区模型。在模型达到初始应力平衡状态后，进行采空区模型的构建。以矿山采空区实际情况为基础，确定构建以下3 个采空区模型:模型1，采空区模型长度为120 m，沿走向每隔15 m 留尺寸为5 m×5 m 的矿柱，采空区宽度为100 m，高度为20 m;模型2，采空区模型长度为120 m，在模型1 的基础上，挖掉采空区中间的1 个矿柱，采空区宽度为100 m，高度为20 m;模型3，采空区模型长度为120 m，在模型2 的基础上，再挖掉采空区中间的1 个矿柱，采空区宽度为100 m，高度为20 m。

(3)模拟3 个模型条件下采空区的稳定性。本次数值模拟根据矿体赋存条件及开采顺序，计算上述3 个模型情况下采空区围岩应力变化状况及采空区顶板的位移状况，同时记录开采时的围岩应力和位移状态，用于分析和研究采空区顶板的应力响应特性，判断采空区的稳定性。

3.3 方案数值模拟

经过分析模拟，得到了剖面的最大主应力云图、最小主应力云图和位移云图等。

(1)模型1，模拟计算按预设矿柱形成采空区的稳定性。模拟按照沿走向方向每隔15 m 留设5 m×5 m 矿柱情况下形成采空区的稳定性，其最大、最小主应力云图和位移云图如图1 ～图3 所示。

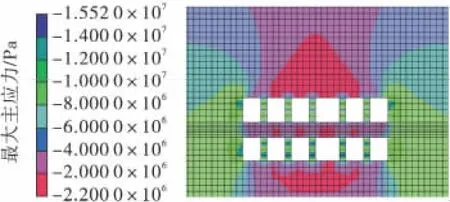
图1 模型1 最大主应力图Fig.1 Maximum principal stress of model 1

图2 模型1 最小主应力云图Fig.2 Minimum principal stress of model 1

图3 模型1 位移云图Fig.3 Displacement nephogram of model 1

由以上数值模拟结果可知，在沿走向每隔15 m 布置尺寸为5 m×5 m 矿柱的情况下，采空区上覆岩层中的最大和最小主应力分布均存有共性，在垂直方向上呈现拱形层状分布，上覆岩层压力传递到矿柱上，矿柱与顶板接触部位应力较采空区中央顶板应力大，而且下部矿柱中应力明显大于上部矿柱中应力，矿柱中最大应力均出现在靠近底板5 m 和靠近顶板5 m 处。该条件下，采空区顶板没有出现拉应力区域，并且上部采空区的顶板应力比下部采空区的顶板应力大，在采空区两帮距顶板1/4 处有应力集中现象。采空区顶板下沉量在采空区形成的初始阶段比较大，后续趋于一定值，在达到二次平衡时顶板最大位移量为2.446 cm，出现在上部采空区顶板中央部位。

(2)模型2，跨度加大1 倍时采空区的稳定性。在模型1 的基础上挖掉中间1 个矿柱，即增大1 倍距离的矿柱间距，形成模型2，计算分析形成的新采空区的稳定性，并与预留矿柱采空区的二次平衡状态做比较。模型2 计算后得到最大、最小主应力云图和位移云图见图4 ～图6。

图4 模型2 最大主应力图Fig.4 Maximum principal stress of model 2

图5 模型2 最小主应力云图Fig.5 Minimum principal stress of model 2

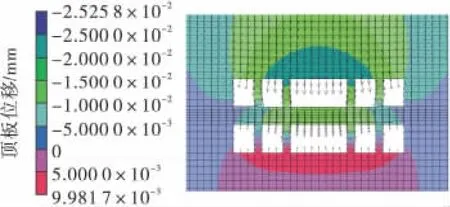
图6 模型2 位移云图Fig.6 Displacement nephogram of model 2

在模型1 基础上，挖掉中间1 个矿柱，加大了采空区跨度，由以上云图可知，在上下2 个中间采空区的顶板中央出现了拉应力。挖掉1 个矿柱后上覆岩层压力产生向相邻矿柱的转移，在此转移过程中，由于顶板上部的压力拱跨度增大，此跨度大于相同条件下合理拱轴线对应拱形的跨度，因此在压力拱内部产生了拉应力，所对应的在上下2 个采空区顶板中央产生了拉应力区域，并且上下2 个矿柱中最大应力区域均变大，表明矿柱中所承受压力增大。在此条件下顶板最大下沉量为2.526 cm，对应部位为上部采空区顶板中央产生拉应力的区域。另外，由图分析可知，两边采空区帮部距采空区顶板5 m 左右处均产生应力集中现象。

(3)模型3，跨度加大2 倍采空区的稳定性。在上述2 个采空区稳定性模拟分析中，加大了矿柱间距，亦即增加了采空区顶板暴露面积。按照模拟分析计划，在模型2 基础上，进一步加大采空区顶板暴露面积，挖掉模型2 中间的1 个矿柱，形成模型3，模拟分析在跨度加大2 倍后采空区顶板暴露面积情况下采空区的稳定性。其最大、最小主应力云图和位移云图见图7 ～图9。

图7 模型3 的最大主应力图Fig.7 Maximum principal stress of model 3

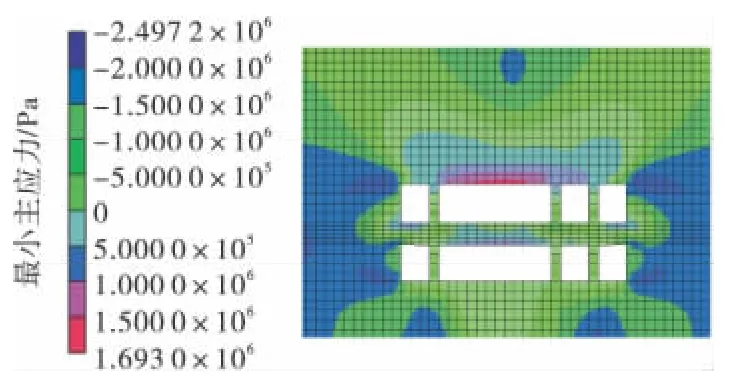
图8 模型3 的最小主应力云图Fig.8 Minimum principal stress of model 3

图9 模型3 的位移云图Fig.9 Displacement nephogram of model 3

在跨度加大2 倍后，采空区顶板应力状态变化明显，由于采空区顶板上面压力拱跨度进一步增大，致使拱内受拉区域范围明显扩大，其中上部顶板暴露面积最大的采空区有58.3%的范围处于受拉伸范围内，下部顶板暴露面积最大的采空区有41.7%的范围处于拉伸状态。顶板最大下沉量为2.55 cm，位于上部暴露面积最大采空区的顶板中央。采空区帮部距顶板5 m 左右出现应力集中现象。由最大主应力云图可以看出，上下2 层矿柱内大应力范围进一步扩大，最大应力部位仍处于矿柱靠近顶板1/4 和靠近底板1/4 处，受力变化明显。

3.4 数值模拟结果分析

(1)支撑采空区的矿柱内压应力随着空区跨度的增大而增大，并且在矿柱靠近顶板1/4 和靠近底板1/4 处应力最大，为15.52 MPa。此值远小于围岩抗压强度(91.33 MPa)，因此按每隔15 m 留设5 m ×5 m 矿柱的情况下，矿柱是稳定的。

(2)当增大1 倍矿柱间距，随着采空区顶板暴露面积的增加，顶板下沉量从2.446 cm 增加到2.526 cm，并且于顶板中央部位产生拉应力区域。当增加2倍矿柱间距后，采空区顶板有58.3%的范围处于拉应力区域，拉应力从1.43 MPa 增大到1.69 MPa，而本矿山方解石的抗拉强度为1.94 MPa，此时顶板受拉安全系数仅为1.1，因此在每隔45 m 留设5 m ×5 m 矿柱的情况下，采空区顶板处于失稳临界状态。

(3)3 个数值模型中，均出现了采空区两帮向采空区内部的位移，数值为5 ～10 mm，并且3 个模型中此数值变化微小。因此认为采空区侧帮位移与采空区顶板暴露面积关系不敏感。

(4)3 个数值模型中，两侧采空区帮部距顶板5 m 左右处的范围均表现出有12 ～17 MPa 的应力集中现象，并且从应力云图可以看出，此3 个模型再次平衡后，应力集中范围相似。

(5)由数值模拟结果可知，模型1 中处于下部采空区中央部位的矿柱内最大应力为14 ～15 MPa，靠近空区两帮的矿柱内最大应力为12 ～14 MPa，并且从应力云图可知，较之靠近空区两帮的矿柱，中央部位矿柱内最大主应力范围更大，模型2 和模型3 也表现出相似的现象。因此，在支撑采空区顶板作用方面，采空区中央矿柱比边矿柱所起作用大。

(6)综上所述，可知沿走向每隔15 m 留设5 m×5 m 矿柱情况下，采空区顶板没有出现受拉区域，这种情况下的采空区处于稳定状态。矿山已经形成的采空区在现有未扰情况下是稳定的。

4 结 论

根据分析结果，矿山采空区在现有跨度小于15 m 并且所留设矿柱尺寸不小于5 m ×5 m 情况下，采空区不经强烈扰动时是稳定的，为后续采空区治理提供了理论依据。并且经过对矿山采空区的现状调查，认为进行的群空区稳定性数值模拟计算分析对类似矿山的采空区稳定性评价提供了参考经验。

［1］ 武崇福，刘东彦，方 志.FLAC3D在采空区稳定性分析中的应用［J］.河南理工大学学报:自然科学版，2007，26(2):136-140.

Wu Chongfu，Liu Dongyan，Fang Zhi.The application of FLAC3Din the analysis on stability of the waste cave［J］.Journal of Henan Polytechnic University:Natural Science，2007，26(2):136-140.

［2］ 彭 欣.复杂采空区稳定性及近区开采安全性研究［D］. 长沙:中南大学，2008.

Peng Xin.Study on Stability of Complex Cavity and Safety in nearcavity Excavation［D］.Changsha:Central South University，2008.

［3］ 钟 钢，韩方建.平水铜矿采空区稳定性数值分析［J］. 金属矿山，2004(3):8-10.

Zhong Gang，Han Fangjian. Numerical analysis of stability of mined area in Pingshui Copper Mine［J］.Metal Mine，2004(3):8-10.