基于弹性薄板理论的采场顶板破断特征分析
王新丰 高明中 陈雨雪 王建建 兰学强 周安伟
(1.煤矿安全高效开采省部共建教育部重点实验室,安徽 淮南232001;2.安徽理工大学能源与安全学院,安徽 淮南232001)
岩层活动与矿山压力联系密切,采场围岩活动是形成矿山压力的根源,矿山压力的显现也是采场围岩活动的具体表现[1]。采矿界众多学者针对采场顶板的破断特征展开了大量研究[2-4],提出了以压力拱、悬臂梁、铰接岩梁、砌体梁及传递岩梁为主的多种岩梁假说。但岩梁理论未能凸显岩层结构的空间概念,为了更加直观获取顶板破断的宏观特征,人们开始尝试用薄板模型来揭示覆岩破断的内在机理与空间形态[5-7],根据不同的支承边界条件建立了采场矿压薄板理论的力学模型,研究了工作面顶板结构破断及裂纹发展的力学特征。然而由于前人对于薄板理论的应用研究大多选取某一特定的开采阶段展开探讨,因此很难全面获取顶板不同时期的破断特征。为了反映顶板破断的连续性和时效性,本研究采用弹性薄板的小挠度理论构建不同开采阶段下的顶板力学模型,从岩层运动的角度揭示顶板破断的失稳机理。
1 顶板破断的力学模型分析
采矿中形成的顶板由于其高长比很小可将其简化为矩形薄板[7],根据采场顶板瞬时破坏、分段延伸和分区迁移的时空特点,对采场顶板构建四边固支、两边固支两边简支和四边简支3 种不同支承边界条件下的力学模型,通过对3 种力学模型的分析求解,可以得到采场顶板不同破断时期的力学演化形态。
1.1 顶板破断前的力学模型分析
采场顶板破断前可将其视为四边固支的矩形薄板,采场覆岩受均布荷载q 作用。矩形顶板长为2a,宽为2b(其中b <a),板厚为h,弹性模量为E,泊松比为μ,抗弯刚度为D,板的挠度为ω,内力弯矩为Mx、My,顶板应力为σx、σy和τxy。建立四边固支的矩形顶板力学模型,如图1 所示。

图1 四边固支顶板力学模型Fig.1 Mechanical model of the roof with four edges clamped
根据题设条件可知,该矩形薄板的边界条件为

基于弹性力学的最小势能原理,利用瑞利-里茨法[8]构建满足边界条件的一阶挠曲面方程

根据薄板弯曲的直法线假设,在不计应变分量的情况下,求得薄板弯曲的总势能为

由(∂EP)/(∂A1)得

进而求得

其中,
D = Eh3/[ 12 (1 - μ2)] .
根据弹性力学的内力弯矩公式[8],求得等厚薄板的弯矩为
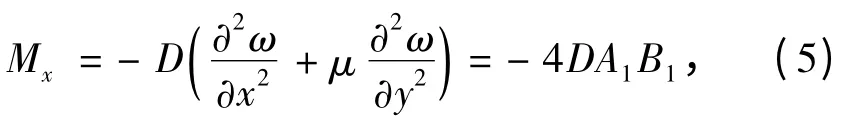
其中,
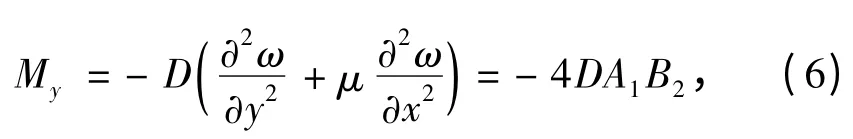
其中,
B1=[( y2-b2)2( 3x2-a2)+μ ( x2-a2)2( 3y2-b2)],
B2=[( x2-a2)2( 3y2-b2)+μ ( y2-b2)2( 3x2-a2)].
利用弹性力学的应力推导公式[8],求得等厚薄板的顶板应力为

采用数学极限求导方法对弯矩式(5)、式(6)进行极值求解,可以得出矩形顶板的弯矩最大值点在长边中点,即点(0,±b)处,此时对应的顶板应力相对较大。因此长边中点处的弯矩值将首先达到岩体的极限弯矩开始发生破断,破断后的裂纹不断向长边两端蔓延扩展,直至破坏到长边边缘。
1.2 顶板破断期间的力学模型分析
矩形顶板的长边破断以后,采场顶板的固支长边将变为简支边,进而构建顶板破坏期间两边固支两边简支的力学模型,如图2 所示。

图2 两边固支两边简支的顶板力学模型Fig.2 Mechanical model of the roof with two edges clamped and two edges simple supported
由题设条件可得,该等厚薄板的边界条件为

同样利用瑞利-里茨法构建满足边界条件的一阶挠曲面方程

进而求得
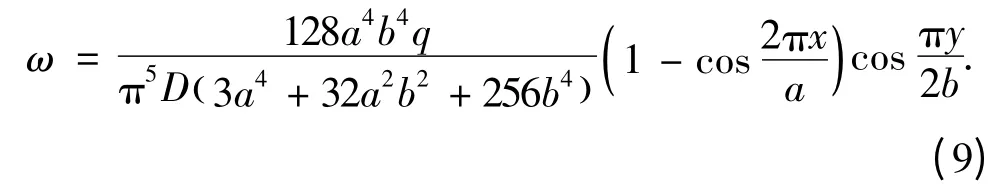
利用弹性力学的内力弯矩公式,求得等厚薄板的弯矩为

同样对弯矩式(10)进行分析求解,得到顶板弯矩的最大值点在短边中点,即点(±a,0)处,此时对应的顶板应力为

该力学模型下的矩形顶板首先在短边中点附近达到其极限弯矩进而发生破断,随着开采的进行断裂裂纹沿着短边中点逐渐向两端扩展,直至将短边完全破断,由原来的固支边转化为简支边,使得顶板内部形成环形破断,近似为平面横“O”型破坏。
1.3 顶板破断后的力学模型分析
随着工作面推进度的增加,当矩形顶板的四条固支边全部破坏为简支边后,顶板破断形式随即改变,因此需重新构建力学模型,依据新的强度破坏准则进行力学求解,新建模型如图3 所示。

图3 四边简支的顶板力学模型Fig.3 Mechanical model of the roof with four edges simple supported
依据题设条件,新建力学模型的边界条件为
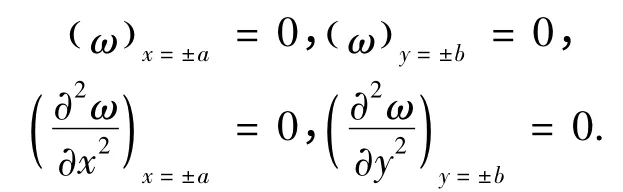
利用里茨法构建满足上述边界条件的一阶挠曲面方程

进而求得满足条件的一阶挠度表达式

利用弹性力学的内力弯矩公式,求得等厚薄板的弯矩为
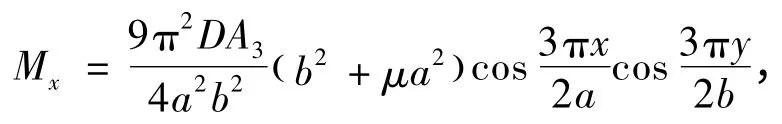
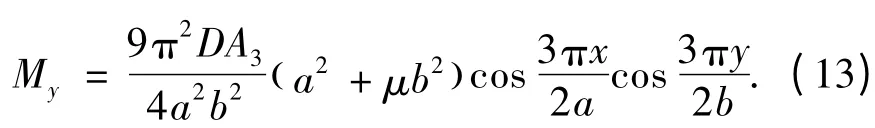
由弯矩式(13)可以求得顶板弯矩的最大值点位于矩形薄板的中心,即点(0,0)处,此时对应的顶板应力相对较大,因此该矩形顶板将在薄板的中心位置发生破断,从而产生沿x 方向的横向裂纹,且裂纹发展趋势随开采进度不断向两端扩展,并在短边近端断裂裂纹产生分叉,形成平面的横“X”型破断。
2 顶板破断的力学特征
采场覆岩的破断特征和垮落形态与开采进度和推进时间密切相关,表现为覆岩破坏的时空效应。通过对不同开采阶段的顶板力学模型分析求解,可以得到顶板破断的力学显现特征和时空演变形态。采场顶板的破断过程随着开采活动的进行经历了以下几个演化阶段:采动伊始,采场顶板首先在长边中点发生破断,破断裂纹不断向长边两端蔓延扩展,直至破坏到长边边缘;随后矩形顶板的短边中点开始破断,并逐渐向两端延展,促使薄板短边完全破断,断裂裂纹与长边端部交合贯通,构成环形破断,形成平面的横“O”型破坏;再随着工作面继续向前推进,顶板中心处发生破断,产生沿x 轴方向的横向裂纹并不断向短边扩展,最后在短边近端断裂裂纹发生分叉延伸,同薄板长边的端角处交合贯通,形成空间的横“X”型破断。顶板四周形成的空间横“O”型破断与中部形成的“X”型破断共同构成了顶板破断的横“O-X”型破坏形态,其顶板破断的演化过程如图4 所示。

图4 采场顶板横“O-X”型破断演化过程Fig.4 The evolutionary process of stope roof with horizontal "O-X "shape fracture
3 顶板应力演化规律的数值模拟
在理论分析采场顶板破断规律的基础上,运用三维数值模拟软件FLAC3D对采场顶板的破断过程进行建模分析。模型的几何尺寸设计为600 m×400 m×200 m(长×宽×高),工作面斜长保持200 m 沿走向推进,推进期间为了避免边界效应对模型开采的影响,走向两边各留100 m 的保护煤柱。煤层埋深约600 m,底板厚度45 m。模型四侧和底部根据具体约束条件固定各边界的水平方向位移或垂直方向位移,顶部定义为自由边界并施加15 MPa 的均布荷载。
通过模拟煤层顶板应力场的演变过程,可以从宏观上窥探顶板应力的分布状态及时空演化规律(见图5)。煤层开采至50 m(图5(a))时,顶板长边首先出现应力集中现象,长边中部的应力显现程度较高,应力峰值集中于长边中点。工作面推进到100 m(图5(b))时,短边中部开始出现应力集中,且应力集中区域由短边中心向端末发展。当工作面推进到150 m(图5(c))以后,顶板中部应力开始显现,并随工作面推进度的增加不断由中心位置向外辐射。随着应力数值不断增大,应力集中现象随之扩展,工作面推进到300 m(图5(f))时应力分布区域几乎覆盖了整个板面。综合分析发现,应力集中出现的部位依次由“顶板长边—短边—中部”循序渐进地向前发展,顶板应力的宏观演变特征与采场顶板的横“O -X”型破断较为吻合,其演变过程类似于顶板的横“O -X”型破断。

图5 顶板应力的演化过程Fig.5 The evolutionary process of the roof stress
4 结 论
(1)针对煤层开采过程中采场覆岩形成的特定空间结构和变形破断形态,运用弹性薄板小挠度理论构建了3 种不同支承边界条件下的顶板力学模型,通过理论计算得出了顶板断裂前后的挠度、弯矩和应力解析表达式,并从理论层面揭示了顶板破断的力学特征,采场顶板首先在板边四周形成平面的“O”型破断,而后在中部形成平面的“X”型破断,两者交合贯通构成顶板的空间横“O-X”型破断。
(2)采用数值模拟软件分析了顶板应力场的分布状态和演化规律,工作面推进过程中顶板应力的集中部位依次由“顶板长边—短边—中部”逐渐向前扩展,其应力演变过程与顶板横“O -X”型破断相互印证。
[1] 张益东,程敬义,王晓溪,等. 大倾角仰(俯)采采场顶板破断的薄板模型分析[J].采矿与安全工程学报,2010,27(4):487-493.
Zhang Yidong,Cheng Jingyi,Wang Xiaoxi,et al.Thin plate model analysis on roof break of up-dip or down-dip mining stope[J].Journal of Mining and Safety Engineering,2010,27(4):487-493.
[2] 史 红,姜福兴. 采场上覆大厚度坚硬岩层破断规律的力学分析[J].岩石力学与工程学报,2004,23(18):3066-3069.
Shi Hong,Jiang Fuxing.Mechanical analysis of rupture regularity of hard and massive overlying strata of longwall face[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(18):3066-3069.
[3] 陈忠辉,谢和平,李全生.长壁工作面采场围岩铰接薄板组力学模型研究[J].煤炭学报,2005,30(2):172-176.
Chen Zhonghui,Xie Heping,Li Quansheng. Study on plate group mechanical model for main roof of longwall face[J].Journal of China Coal Society,2005,30(2):172-176.
[4] 钱鸣高,石平五.矿山压力与岩层控制[M].徐州:中国矿业大学出版社,2003:66-70.
Qian Minggao,Shi Pingwu.Mining Pressure and Stata Control[M].Xuzhou:China University of Mining and Technology Press,2003:66-70.
[5] 贾喜荣,翟英达.采场薄板矿压理论与实践综述[J]. 矿山压力与顶板管理,1999,16(3/4):22-25.
Jia Xirong,Zhai Yingda.The review of groundpressure theory of thin slab in coal mining and its application[J]. Ground Pressure and Strata Control,1999,16(3/4):22-25.
[6] 顾 伟,张立亚,谭志祥,等. 基于弹性薄板模型的开放式充填顶板稳定性研究[J]. 采矿与安全工程学报,2013,30(6):886-891.
Gu Wei,Zhang Liya,Tan Zhixiang,et al. Study on roof stability of open backfilling based on elastic plate model[J].Journal of Mining and Safety Engineering,2013,30(6):886-891.
[7] 浦 海,黄耀光,陈荣华.采场顶板X -O 型断裂形态力学分析[J].中国矿业大学学报,2011,40(6):835-840.
Pu Hai,Huang Yaoguang,Chen Ronghua.Mechanical analysis for XO type fracture morphology of stope roof[J]. Journal of China University of Mining and Technology,2011,40(6):835-840.
[8] 吴家龙.弹性力学[M].北京:高等教育出版社,2001.
Wu Jialong. Elasticity Mechanics[M]. Beijing:Higher Education Press,2001.

