基于时间序列小波分析的产出缺口估计
□文/张鹏飞
(新疆财经大学 新疆·乌鲁木齐)
产出缺口是指实际产出与潜在产出的差值占实际产出或潜在产出的比率,它测度的是实际产量与经济中现有资源充分利用所能生产的产量之间的差额,反映现有资源的利用程度,其中潜在产出即充分就业时的理想产出水平。如果实际产出大于潜在产出,就意味着总需求大于总供给,央行就应当紧缩货币;如果实际产出小于潜在产出,则意味着总供给大于总需求,那么央行就应当扩张货币,以降低有效需求不足引起的通货紧缩风险。在长期,政策制定者须以潜在产出为基础制定货币政策,这样才能指向可持续发展的目标,避免经济起伏不定。
一、产出缺口方法的选择
产出缺口无法直接观测到,唯有估算得出。近些年来,国内外这方面讨论逐渐增多,许多估算方法得到应用。据Konuki(2008)指出,目前通用的估计产出缺口方法有三类:生产函数法、单变量法和多变量法。如果把这些估计方法按照时间序列来区分,上述三类方法可归结为两大类:直接分析数据随时间变化的结构特征,即时域分析;把时间序列看成不同谐波的叠加,研究时间序列在频域里的结构特征,即频域分析。
其中时域分析的方法包括早期的线性趋势分解法、一阶差分分解法、生产函数法、结构式向量自回归(SVAR)法。生产函数法与结构向量自回归法对数据的要求比较高,使用不多,张建(2007)、Chow(2002)利用该方法估算出我国的产出缺口,这一方法要求生产函数是稳定的;郭红兵(2010)、赵昕东(2008)利用SVAR 法估计我国产出缺口,而这种方法有失业率与实际产出之间存在稳定关系为前提的假设。市场是一个日新月异的动态系统,政策更新、经济转型、技术进步、金融创新等都会使投入产出关系变化,这样各交叉变量间的关系将不再稳定,将造成计算结果存在误差(Wen and Zeng,2005)。
通过频域分析估算估计产出缺口的方法中常用的有HP滤波、BK 滤波、Kalman 滤波等。滤波方法可以将实际产出分解为趋势成分和周期成分,其中趋势成分即潜在产出,周期成分就是产出缺口。通过滤波的方法(许召元(2005)、谢太峰(2008)、Gerlach&Peng(2004)等)计算产出缺口的文献比较多,这一方法优势在于简单易行,如果实际产出的分解方程与滤波混合使用将得到理论上强有力的支撑,而且滤波方法也不要假定协方差不变。实际上,如果把时间序列看成由不同频率的正弦波或余弦波叠加而成,在频域上比较不同频率波的方差大小,通过研究和比较各分量的周期变化,分析该时间序列的频率结构与波动特征。这一方法需要以傅立叶变换为基础,这一变换就是将时间序列从时域映射到频域的一种工具,过程如下:

这里X(t)表示原始时间序列形式,z 表示频率。这一变换的实质是把f(x)的波动分解成许多不同频率的规则波的叠加,通过计算f(x)和复指数函数e-2iπkt间的相关系数,就可以将对原函数X(t)的研究转化为对其相关系数F(z)的研究。通过傅立叶变换可以求得各种滤波算子,从而将所有频段分解为趋势成分和周期成分。与前面的一阶差分法分解趋势成分和周期成分相比,滤波不会放大非主流信息,因此有很强的优越性。但是这并不能掩盖该方法的重要缺陷:由时域转换到频域的过程中丢失了时域信息。如果这是一个平稳的时间序列,变量之间的关系是稳定的,那么这个缺陷就不重要,但是产出缺口的估计确是要计算不稳定变量间的差值,因此滤波方法会在计算的过程中产生误差。
这就需要寻找一种新的方法,尽可能少地丢失时域和频域的序列特征,时间序列小波分析方法很好的解决了上述方法的缺陷,不仅能够在时频两域的窗口加以改变,而且在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率,这让我们能够根据实际需要在时间精度与频率精度之间进行适当的取舍。所以本文在估计产出缺口时采用时间序列小波分析方法,这一方法在信号降噪领域得到广泛应用,但是在经济学中的应用尚处于探索阶段(Crowley,2007),Jagric and Ovin(2004)利用小波分析研究经济周期;国外最早使用小波方法研究产出缺口的是Scacciavillani&Swagel(2002)和Conway&France(2000)分别估算出以色列和新西兰的产出缺口,而国内杨天语和黄淑芬(2010)利用这一方法估算出1992~2009 的季度产出缺口,纵观以上研究,均是对年度数据或季度数据的估算,而本文将对月度产出缺口进行估算。
时间序列小波分析估算产出缺口的基本原理是:先将实际产出自然对数序列Yt看作原始信号,将它分离出趋势部分与周期部分,其中趋势项是潜在产出Y*t,周期项是产出缺口ηt,公式表示为:
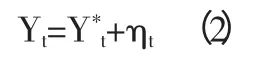
ηt为周期部分,对产出没有长期影响,因而可以看作是“噪声”。具体地说,如果我们将潜在产出序列Y*t看成是一个信号f(t),将s(t)看作是包含原始信号的实际产出序列Yt,e(n)看作是周期成分或产出缺口ηt,则上式就可以表示为一个噪声模型:

其中σe(n)为噪声,σ 为噪声强度,当σ=1 时,e(n)为高斯白噪声。其基本原理为通过小波变换抑制噪声ηt,以从产出Yt中提取出不可观测的潜在产出Y*t,再计算出产出缺口Yt-Y*t,这一过程被称为小波降噪。要实现这一过程,需先进行小波变换,这是一种利用小波变换实现降噪的方法,他主要通过多级小波分解将信号分解为一个近似信号和若干个细节信号,然后在细节信号上加以处理,最后再把分解后的信号逐级重构回去,就得到降噪信号了,细节信号处理的主要使用门限滤波,也就是细节信号中过滤掉强度小于门限值的成分。
其中,原始信号即实际产出Yt,而重构回的信号即潜在产出Y*t,那么通过上述过程,就可以计算出公式2 中的潜在产出和产出缺口序列。
二、产出缺口估计
本文使用2006~2013年GDP 数据,名义GDP 季度数据与同比CPI月度数据来自国家统计局网站,并由规模以上工业增加值增长率估算出月度名义GDP;2011年及之前GDP 平减指数由《2013年中国统计年鉴》中数据计算得出,2011年之后GDP 平减指数根据GDP年增长率及以2005年为基期的GDP数值计算得来,因为GDP 平减指数比CPI 更精确地平减现价GDP 数据,所以本文将定基CPI月度数据作为引导序列,使用Matlab2012a 实现三次Hermite 插值法把年度GDP 平减指数插值为月度GDP 平减指数,然后将现价GDP 换算为以2005年为基期的不变价格GDP 序列。由于月度数据含有很强的季节特征,因此先用Eviews6.0 对数据进行Census X12 调整,再采用Origin8.0 软件实现小波降噪的计算。
对于月度名义GDP 的计算,假设1 季度2月相对于1月规模以上增加值增长率为a,3月相对于2月的增长率为b,并设1 季度名义GDP 为100,则对1月份名义GDP 通过如下公式估算:

那么,2月、3月GDP 分别为:

以名义GDP 通过GDP 平减指数得到实际GDP 的计算公式为:

如图1 为以2005年为基期的月度实际GDP 与通过Census X12 调整后的月度GDP,可以看到调整后的数据更加平稳,波动远没有调整前剧烈,但从2008年下半年开始,调整后的数据依然有小幅波动,这表明当年实际经济受次贷危机影响较大,但是依然呈现上升趋势。(图1)

图1 以2005年作为基期的月度GDP
对于Census X12 季节调整后的数据使用小波降噪。在具体操作中:首先,我们考虑不同的小波基函数,通过不同的小波基函数的特性观察降噪效果;其次,在拓展模式中,本文选择周期性拓展,对于门限滤波级数的确定,本文采用3~5 级,这是因为级数越多,被过滤掉的细节信号就越多,降噪也就越彻底,有利于更深层次的信号趋势分析,时间序列更平稳。但是,如果级数过多,也会出现失真的情况,计算量也成倍增加,因此本文采用3~5 级门限滤波;再次,对门限值,其单位是相当于每节细节信号的百分比,值越大,降噪越彻底,但如果门限值太大,反而会把决定趋势的因素过滤掉,所以应尽量避免结果失真的情况。
针对以上问题,本文采用不同的小波基函数,不同的门限滤波级数和门限值的组合对月度GDP 序列降噪。由于小波基函数不是唯一的,并且本节的研究对象是精确估算实际月度产出缺口,因此分别试验Haar 小波,2~10 阶DB 小波,以及1~3阶具有低通重构滤波的Biror 双正交小波等多种小波基函数进行试验。用上述小波基函数做不同门限级数的降噪,然后重构,然后放弃那些重构信号明显与原信号存在差别的小波基函数。因为如果重构后信号与原信号差别较大,那意味着经重构后得到的GDP 序列与小波降噪之前的原GDP 序列差别较大。
经过试验,Haar 小波,bior1.1 小波经降噪重构的GDP 与经季度调整后的实际GDP 序列的差别最小,上述两种小波基函数计算结果与原序列的标准差值最小的是Bior1.1 基函数,所以本文应用Bior1.1,Periodic,门限级数:5,门限值:30%的组合,估算月度产出缺口如图2。(图2)
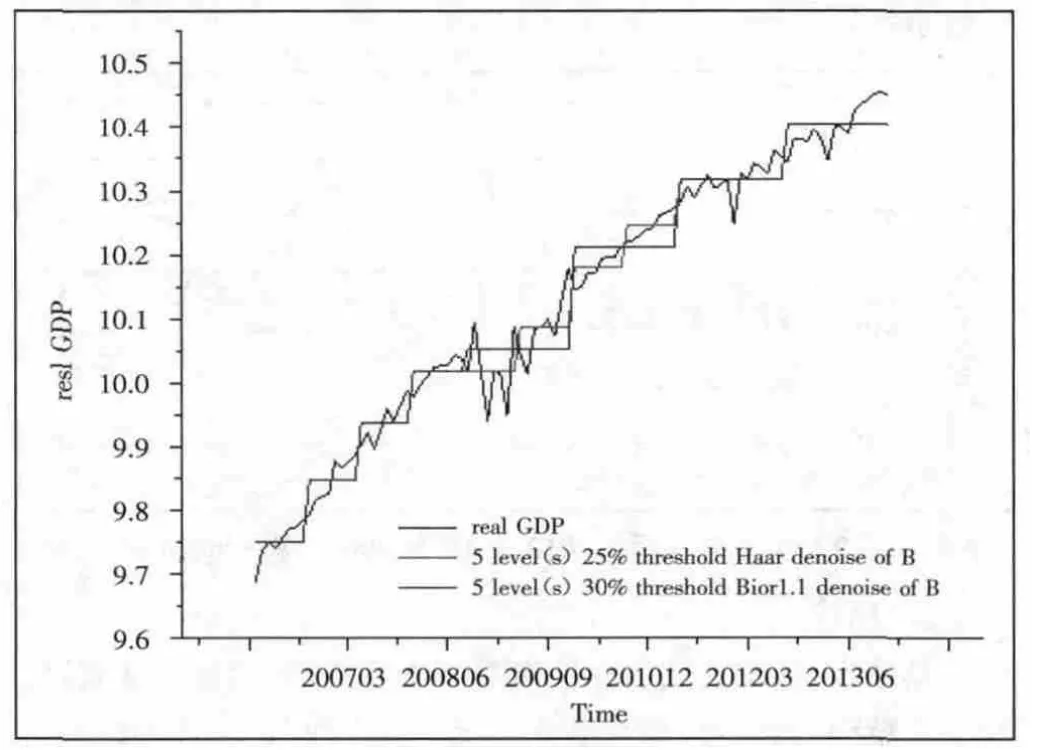
图2 Haar(5,25%)、Bior1.1(5,30%)和真实GDP对比
从图3 可以看出,与已有的年度、季度数据估计结果(赵昕东,2008;杨天宇、黄淑芬,2010)相比,用月度数据估计的潜在产出波动更加频繁,因此揭示了很多年度、季度数据估计无法显示的产出缺口,这表明利用月度数据的产出缺口估计结果更加精细。具体来看,从2006年1月至2013年12月,小波降噪的月度数据产出缺口出现了21 次正负值转换,而赵昕东(2008)估计的1982~2006年度数据产出缺口只出现了7 次正负值转换,虽然杨天宇、黄淑芬(2010)利用从1992年一季度到2009年一季度的季度数据估计产出缺口估计出了22 次正负值变化,但这是超过17年的数据,而本文只用了8年的数据,可以看出本文的估计结果更为精确,可以揭示出更多、更精细的经济波动。(图3)

图3 2006年1月~2013年12月GDP月度产出缺口
三、结论
具体来说,本文的估计结果有如下特点:周期波动频繁,时间更为精确。与年度、季度数据相比,月度数据在同样的时间跨度下估计的产出缺口波动更加频繁,正负值交替更多。
金融危机后,波动周期时间更长。2010年之前,我国产出缺口交替较为平稳,大概9~10 个月完成一次短周期,周期不足一年;2010年之后,周期长度变成了15~16 个月,周期超过一年。短期经济周期时间拉长,意味着产出缺口波动频率降低,而这一现象也存在于发达国家,但与发达国家容易出现经济周期稳定化的特点相比,发展中国家经济周期不稳定更加明显,原因是发达国家的技术领先优势使得他们的产品有更强的市场支配力量和更低的价格需求弹性,因此发达国家受需求冲击的影响较小;而发展中国家没有这样的优势,经济容易收到世界主要大国经济波动的影响,经济抗压能力弱,本国没有议价能力,因此受到冲击的概率明显上升。我国作为发展大国也存在上述问题,却依然出现了波动周期时间变长的情况,这就意味着经历经济危机以后,我国社会主义市场经济更加完善,市场调节能力上升,宏观调控手段更加成熟,时机把握娴熟,国内需求扩大抵消了国际市场需求量的减少,从而缓解了产出缺口的波动。
[1]姚恩营.基于多尺度小波分解的时间序列预测方法研究[J].计算机时代,2009.1.
[2]杨天宇.基于小波降噪方法和季度数据的中国产出缺口估计[J].经济研究,2010.1.
[3]谭屹然,石柱鲜.小波分析模型在经济领域中的应用[J].工业技术经济,2010.12.
[4]张健,何彬.产出缺口的生产函数法估计及经验分析[J].黑龙江社会科学,2007.2.
[5]刘斌.我国产出缺口的估计[J].金融研究,2001.10.

