分段幂函数模型在气敏检测器定量算法中的应用

黄 兵，曹 建，范竞敏

(1.中南大学 物理与电子学院，湖南 长沙410083;2.北京华电云通电力技术有限公司，湖南 长沙410000)

0 引 言

随着国民经济的快速发展，工业生产环境中的微量可燃气体的监测越来越重要，如煤矿瓦斯气体监测(主要成分氢气、甲烷、一氧化碳)、变电站油中溶解气体(主要成分氢气、一氧化碳、甲烷、乙烯、乙烷、乙炔)分析等。上述气体的监测对保证工业生产的安全性和国民经济的健康发展具有重要的意义。

目前，在微量可燃气监测中，半导体气体传感器应用较多［1～3］。传统的半导体气体传感器气体定量方法主要是基于半导体气体传感器电导率随气体体积分数呈单调关系的特点［4］，采用电阻直接定量法进行定量。由于随着使用时间增长和周围环境的变化，传感器本身会出现老化现象，其电阻值会出现漂移，从而导致随着时间的增加，检测器的测量误差变大、适应性变差的问题。

针对上述问题，本文通过对半导体气体传感器进行的大量测试，并结合特性曲线进行深入分析，提出了新的电路模型，采用将半导体气敏检测器在分别有、无敏感气体通过时的电阻比值作为特征量的方法，将电阻比转换为输出信号［5］，并由此构建了输出信号与气体体积分数之间的分段幂函数模型。本文方法定量的准确性不受半导体气体传感器出现老化现象和周围环境变化导致的电阻值漂移的影响，具有检测准确性高、环境适应强的优势。实验研究表明:该方法检测数据准确度达到10-7，误差在3%以内。

1 半导体传感器原理与特性曲线分析

半导体传感器物［6］检测原理是:在一定温度条件下，当传感器置于以空气为载气的氛围中时，传感器表面在空气中吸附氧分子，氧分子在半导体表面获得电子而形成O-，O2-等受主型表面能级，导致传感器面电阻增加。如果传感器表面有H2，CO，CH4等可燃性气体流过时，与吸附在半导体表面的氧发生化学反应并伴随着电荷转移，导致半导体的电阻变小，通过测量半导体变化就可以实现对气体的检测。

在检测敏感气体时，半导体气体传感器［7］的电导率随气体体积分数的变化而变化。图1 所示为被测气体体积分数与灵敏度(RS/R0)的关系，其中，R0为无敏感气体通过时半导体气体传感器的阻值，RS为敏感气体通过时半导体气体传感器的阻值。

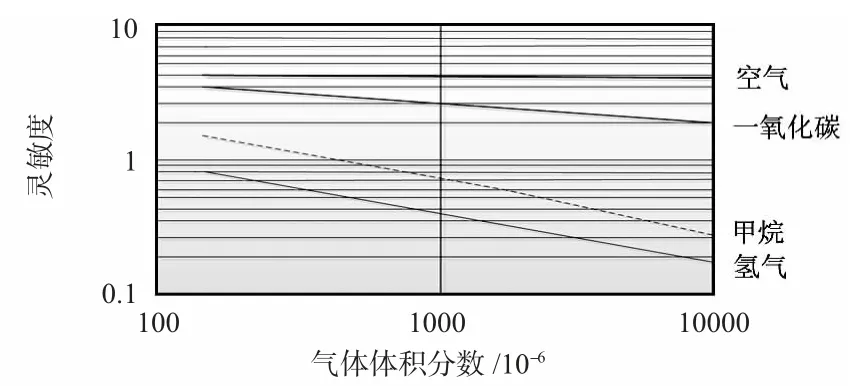
图1 半导体气体传感器灵敏度特性Fig 1 Sensitivity characteristics of semiconductor gas sensor

在实际应用中，一般情况下没有直接测量RS/R0方法，而通过设计相应的电路可将电导率的变化转换为与该气体体积分数相对应的电信号。

采用一种简单的模型:采用电阻分压电路，将采样电阻器和半导体气体传感器串联在总电压为U(单位:V)电路中构成检测电路。在保持半导体气体传感器温度恒定的条件下，测量分压电阻器的电压作为采样电压。在检测前，通过温控模块持续加热2 h 使传感器温度稳定在50±0.1 ℃。

假设无敏感气体通过时，半导体气体传感器的阻值为R0，采样电阻器的电阻值为RB，采样电压值为UB0;当检测到敏感气体时，半导体气体传感器的电阻就会减少，此时的电阻大小为RS，根据串联电路的特点，采样电压就会变大，此时采样电压为UBS。采样电路如图2 所示。

图2 采样电路Fig 2 Sampling circuit

根据电路的特点，可以得出

同时，根据分压电路的特点，得到

由式(1)～式(3)不难得出

其中，UR0为无敏感气体通过时半导体气体传感器两端的电压，URS为敏感气体通过时半导体气体传感器两端的电压。

当RB取值较小，且R0，RS≫RB，此时可以看作

参考图1 灵敏度特性图，对半导体型气体传感器气敏特性曲线［8，9］分析，构建了C=K(R0/RB)A+B 的函数。研究表明，这个函数基本符合半导体型气体传感器检测浓度和电阻之间的关系，也符合幂函数曲线特性。在实际测试中，将R0/RB转换为UBS/UB0。当检测高体积分数气体时，半导体型气体传感器的电阻会变得很小，此时RS，RB之间关系不满足RS≫RB关系，所以，气体体积分数与电阻比之间不符合完全幂函数的关系。

2 气体检测

2.1 检测装置

由于半导体气体传感器对多种气体敏感，如果环境中有多种敏感气体存在，气体检测中容易产生交叉感测，通过色谱分离技术将各敏感气体组分按时间有效分离，再使用后端的气体传感器实现气体含量的检测［10］，避免相互影响。

检测装置主要包括主控单元、调理板单元、数据处理单元等电路构建如图3。

图3 检测系统框架Fig 3 Framework of detection system

控制电路模块获取供电和控制信号来维持传感器的正常运行，使检测电路处在最佳运行状态，再将各种信号输入调理板。

调理板模块的功能是从控制电路模块中获取输出电压信号，经调理板的转换或放大电路处理成适当等级的电压信号，集成信号调理、继电器控制和通信转换等再输入至数据采集进行信号采集。

数据采集与处理模块功能:一方面维持整机的独立正常工作，完成采样、控制、自检、数据存储等功能;另一方面，与主控电脑以网线或双绞线连接进行实时通信，解析并响应上位机的指令包。

2.2 定量算法模型

由于采用精密电阻器和半导体型气体传感器构成分压电路，以电路测量到的电压值作为输入量，若将上述推导函数公式得到的UBS:UB0的比值计为峰高比，设UBS/UB0=X。结合特性曲线得出的结论，此X 和半导体气体传感器的检测气体体积分数并不是完全幂函数关系，也不是线性关系。

在每进行一个检测气体标定时，传感器需要加热时间和采样时间都相对很长，不可能进行大规模的数据探测用来拟合曲线。此外在传感器只探测到2 个位置情况下，如果采用线性曲线来直接拟合，经过线性曲线拟合得出的曲线轨迹只是由2 个位置所确定的直线，显然计算精度并不理想，如果采用全局幂函数曲线拟合，根据对传感器特性和检测电路的分析，在高体积分数情况下，误差会很大。所以，理论上采用分段幂函数作为基函数进行曲线拟合误差会相对较小。

一般情况下，在选取分段点时，考虑到分段后要使相邻曲线连续，即边界点连续这一约束条件

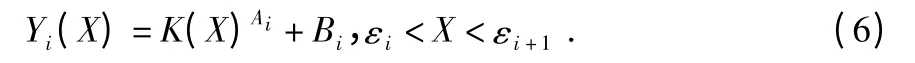
其中，K，A，B 为参数，εi为参考值。

分别求分段幂函数的一阶导数和二阶导数，由

使分段函数式单调增函数;由

使分段函数在分段点连续;由

使分段函数呈凹函数。

2.3 优化曲线算法

在优化曲线拟合中，最小二乘法是一种经常使用的方法。通常最小二乘法适用于做线性拟合［11，12］，其表达式一般为

而本文所建立的函数模型是幂函数，自变量和应变量之间内在的关系呈非线性关系。结合两者关系，采用把线性拟合曲线中的自变量和因变量看成是其它变量的函数，即

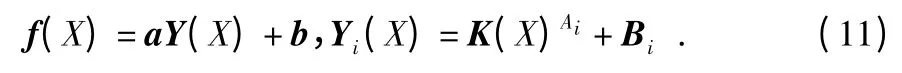
从而将幂函数非线性转化为了线性函数，使之符合最小二乘的线性关系。最小二乘法矩阵表示［13］为

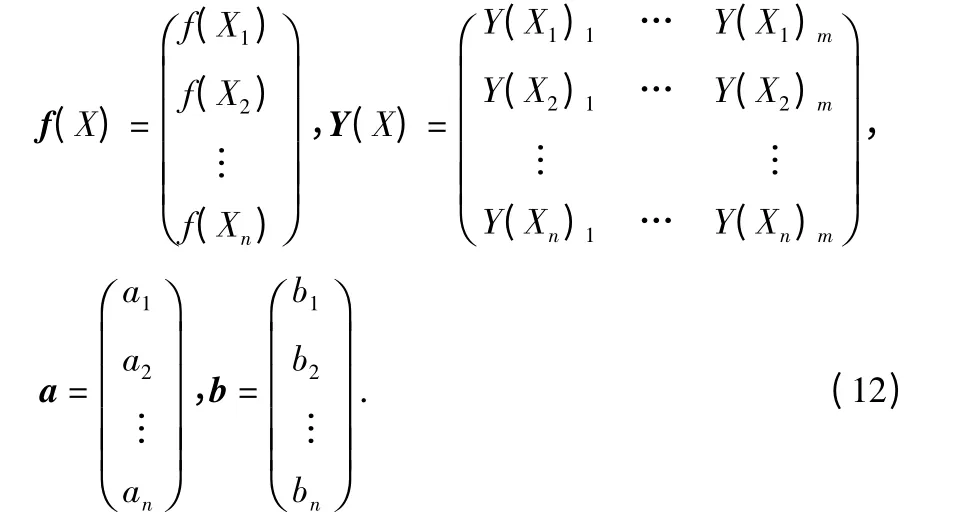
由于观测值不可避免地存在误差，也受噪声干扰，需要通过更多观测值来评估模型的回归系数向量a。n ＞m 时，线性方程组个数大于回归系数的个数，不可能找到满足所有的n 个方程的解，而只能从许多近似解中找到一组使方程组的残差平方和最小的估计的解

3 实验结果

3.1 模型验证

根据对半导体气体传感器特性曲线分析和推导出来的函数关系，同时为了方便比较，在拟合函数上，分别采用了线性拟合、分段幂函数拟合两种方法。图4 即为运用分段幂函数拟合的方法得到的拟合曲线和原始曲线(真实值与峰高对应点连接折线)、线性拟合的对比图。

从图4 可以看到，采用分段幂函数，在气体体积分数较低的条件下，拟合曲线与原始曲线重合度很高，而线性函数拟合的效果，与原始曲线对比误差很大。采用分段幂函数，单独使用高体积分数采样点拟合得出的曲线，也比较接近真实值。从图4 可以看出，拟合曲线不管在低体积分数还是在高体积分数与原始曲线重合率很高。

图4 分段幂函数拟合曲线Fig 4 Fitting curve of piecewise power function

3.2 实验测试

本文选用甲烷气体作为代表气体进行实验，其他气体的测量方法类似。分别对6 种不同体积分数进行定标，测出在不同体积分数下，电压峰值UBS和在没有甲烷通过时的稳定电压(基线电压)UB0，将得到其中5 组峰高比(UBS/UB0)和对应的气体体积分数真实值运用分段幂函数曲线拟合方法进行拟合，利用最小二乘法函数对曲线优化，然后根据拟合曲线进行自身数据检测，由峰高比计算剩下一组气体体积分数，得到气体体积分数实验值，与标称值比较，计算出相对误差。甲烷体积分数拟合实验值和真实值比较如表1 所示。

表1 甲烷体积分数拟合实验值和标称值比较Tab 1 Comparison of experimental value and real value of methane volume fraction fitting

4 结束语

智能化已成为科技时代的主流，智能精确地安全监测成为家庭智能化、变电站智能化等不可或缺的部分。所以，传统的报警监测已经满足不了需求，实现高精度、远程以及实时监测具有重要的意义。利用气体传感器灵敏度特性，运用分段幂函数拟合计算气体精确度达到10-7，实现动态分析气体成分的走向，可以预测安全状况，方便提前做出对应措施，避免危险发生。

［1］ Chang Yanhong，Yao Yunfeng，Wang Bin，et al.Reduced graphene oxide mediated SnO2nanocrystals for enhanced gas-sensing properties［J］.Science China:Technological Sciences，2013，29(2):157-160.

［2］ 梅军鹏，张覃轶，韩雪亮.Mn 掺杂纳米SnO2的气敏性能研究［J］.传感器与微系统，2013，32(1):76-78，82.

［3］ 刘 阳，李 勃，姚有为，等.改善SnO2气体传感器气敏性能的研究进展［J］.传感器与微系统，2012，31(12):5-8.

［4］ 禹春生，王朝晖，焦斌亮.具有无线收发功能的可燃气体检测装置［J］.传感器与微系统，2010，29(6):118-119，127.

［5］ Takao N，Toshimasa K H，Yoshitake Y，et al.Impedance characteristics and data processing for stomach regions for simple and complex meals using scintigraphy［J］.IEEE Transactions on Nuclear Science，2002，49(5):2328-2331.

［6］ 邓立三.气体检测与计量［M］.郑州:黄河水利出版社，2011:92-96.

［7］ Xu Hongya，Cui Deliang，Cao Bingqiang.Effect of nanoparticle size on gas-sensing properties of tin dioxide sensors［J］.Chemical Research in Chinese Universities，2012，28(6):1086-1090.

［8］ 刘天模，曾 文.纳米SnO2-TiO2复合材料的氢敏性能及气敏机理［J］.功能材料，2009，40(7):1229-1232.

［9］ 王彩君，吴兴惠.气敏传感器线性化电路的设计［J］.传感技术学报，1996，12(4):23-26.

［10］丁家峰，罗 安，胡志坤，等.固体氧化物燃料电池的气体检测特性［J］.浙江大学学报:工学版，2012，46(6):1008-1013.

［11］焦竹青，熊伟丽，张 林，等.基于曲线拟合的无线传感器网络目标定位算法［J］.东南大学学报:自然科学版，2008，38(9):249-252.

［12］乔立山，王玉兰，曾锦光.实验数据处理中曲线拟合方法探讨［J］.成都理工大学学报:自然科学版，2004，31(2):91-95.

［13］王贵增，叶 昊.主元分析与偏最小二乘法［M］.北京:清华大学出版社，2011:25-33.