自适应多趟聚类在检测无线传感器网络安全中的应用*

滕少华，洪 源，李日贵，张 巍，刘冬宁

(广东工业大学 计算机学院，广东 广州510006)

0 引 言

数据库技术的快速发展和数据库管理系统的广泛应用，使得各种组织结构积累了海量数据。人们迫切希望从海量数据中找到有用的知识和信息，从而在市场竞争中抢占先机。面对这种挑战，数据挖掘技术获得了迅速发展，不仅在理论上有众多成果［1，2］，且已广泛走向工业应用。聚类分析是数据挖掘的主要方法之一［2］，它是分析数据并从中发现信息和知识的一种手段。对聚类分析，人们取得了一系列研究成果。K-Means 算法［3］是经典的聚类算法之一，但需要预先给定聚类个数和初始值，开销大且对数据输入顺序敏感;文献［4］提到的Rock 算法是一种经典的层次聚类算法，针对包含分类属性的数据集使用链接(两个对象间共同的近邻数目)，不但考虑了对象间的相似度，还考虑了邻域信息;改进的DBSCAN 算法［5］是一种基于高密度联通区域的基于密度的聚类方法，可以有效地找出任意形状的簇。

无线网络传感器［6］作为一种检测装置，能够获得周围的信息，并将这些信息按照一定的规律转换为其他需要形式的信息，满足传输、存储等功能。通过无线传感器收集的信息，这里成为无线网络数据集，本文在提出了自适应的多趟聚类分析方法，并将其运用到无线数据中，发现数据特征，寻找离群信息，对于一般的离群点，往往有重要研究价值，可以用于研究无线传感器节点的安全信息［7］。

1 KSummary 算法

1.1 KSummary 算法与相关概念

KSummary 算法［8］能够处理分类属性与混合属性数据，提出使用聚类摘要信息(cluster summary information，CSI)来表示一个簇，算法给出了自己的相似度计算方法。

设D 为数据集合，D 中任意一条记录有m 个属性，其中有mc个分类属性和mN个数值属性，显然满足m=mc+mN。用Di表示第i 个属性取值的集合，x=2。下面给出KSummary 算法的定义［9］:

定义1 给定簇C，a∈Di，a 在C 中关于Di的频度定义为C 在Di上的投影中包含a 的个数

定义2 给定簇C，n=|C|表示C 的大小，C 的CSI 定义为CSI={n，summary}，由数值型属性的质心和分类属性中不同取值的频度信息两部分组成，即

定义3 设C，C1，C2为数据集合D 划分的簇，p=［p1，p2，…，pm］，q=［q1，q2，…，qm］表示两个对象，x ＞0。

1)对象p 到簇C 的距离d(p，C)定义为p 与簇C 的摘要之间的距离

对于dif(pi，Ci)，当Di表示分类属性时，该值定义为p与C 中每个对象在属性Di上的距离的算术平均值，即

当Di是数值属性时，定义为

2)簇C1和簇C2间的距离d(C1，C2)定义为两个簇的摘要间的距离

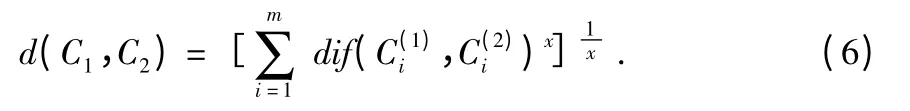
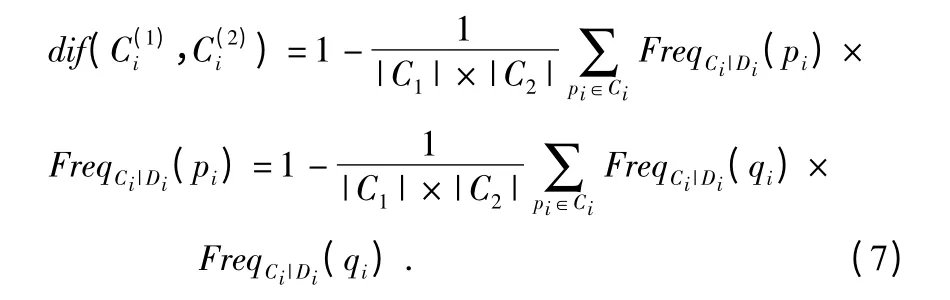
若Di为数值属性，则该值定义为

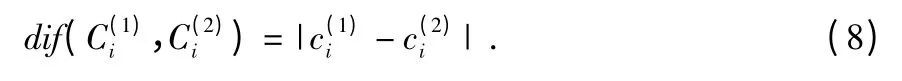
3)dif(pi，qi)表示两个对象p，q 在属性Di上距离，dif(p，q)表示对象p，q 之间的距离

a.若Di是二值属性或分类属性或:

当pi=qi，dif(pi，qi)=0;

当pi≠qi，dif(pi，qi)=1 .

b.若Di是顺序属性或连续数值属性

c.两个对象p，q 间的距离为

1.2 KSummary 算法的不足

KSummary 算法能够很好地处理混合型数据集［9］，但需要解决下列问题:1)预先给定聚类个数k 值，k 的取值直接影响聚类结果;2)需要随机选择k 个初始聚类中心，记为集合Q，但是KSummary 算法的聚类结果对Q 存在依赖关系。

2 自适应多趟聚类分析方法

2.1 体系结构

本文提出自适应多趟聚类分析方法，采用层次聚类、基于密度聚类和KSummary 聚类算法相结合的思想，对数据集进行多趟聚类。多趟聚类体系结构如图1 所示。

2.2 自适应层次聚类

本阶段在层次聚类的基础上，使用自适应［10］层次聚类算法。实施时，对于数据集，根据公式(11)，给出阈值R，R值会选择的相对大些，这样在调整阈值时可以直接减小该值。通过计算簇内和簇间对象的相似度，得到一个评价函数。

若评价函数偏高，则减小阈值R，继续刚才的聚类，得到新的层次聚类，直到评价函数［2］的值达到理想条件为止，这样获得聚类结果依赖于具体的数据集，使得算法更实用和可靠。

算法阈值［11，12］R 定义为

其中，total(D)为数据集D 中对象间的距离之和，n 为指对象个数，α 为阈值调节系数。对于不熟悉的数据集，α值一般都是要通过经验值来获得。

文中使用均衡化的评价函数［11，12］，对于聚类C 计算类内相似度D(C)和类间相似度L(C)，获得了评价函数为

当满足距离代价最小时，可以得到最优的空间聚类结果。自适应层次聚类的流程图图2。

2.3 密度聚类与迭代过程

本文使用的密度聚类［2］方法是在已经有一组聚类基础上进行的。用D 来表示数据集，Ci(i=1，2，..，k)表示簇。本阶段通过计算各个簇中对象密度，选择簇中密度相对较大的点作为该簇的代表点，并选为下一步算法的初始聚类中心。将簇Ci中的任意对象pi的密度定义为density(pi)［11，12］

图2 自适应层次聚类流程Fig 2 Flow chart of adaptive hierarchical clustering

其中，x 为pi所在簇中的对象个数，pj为该簇内对pi有影响的的任一对象，d(pi，pj)为pi到pj的距离，∂为对象之间可以相互影响的阈值。对象pi密度是在该对象所在的簇内计算，因而，阈值∂仅和该簇内对象有关，不同簇中的∂值也是不同的。

获得初始聚类个数k 和初始聚类中心Q 以后，运用KSummary 算法，重复迭代，不断更新簇的摘要信息和对象所属的簇，直到每个对象所属的簇不再发生变化时，算法终止。

2.4 传感器数据集

使用无线传感器收集手机通信信息，从传感器收集的信息要经过多重处理，包括数据压缩和融合等［13，14］，这样在经过处理后会产生能够使用的数据集，这样的数据集适用于自适应多趟聚类算法。数据集的主要属性包括:移动信号强度(MSPOWER)、上行接收信号(RXLEV)、时间延迟量(TA)等。数据集的每条记录，都有标记其来源的若干属性，这样在聚类后，记录位置变化后，仍能找到获得该记录的传感器设备，这样的数据特征有助于分析实验结果。

数据集经过数据预处理［15］后，能够获得切合实际并且适合聚类方法的数据集，部分数据如下

3 实验结果和分析

3.1 实验环境

本文使用了无线传感器收集数据，用于接收手机发出的无线电信号。数据处理和聚类算法使用在机器为:CPU:Inter Core(TM)T5800，RAM:2GB，32 位操作系统。工具为Weka 3.7，Vs 2010.使用精度、平均评价函数、统计方法［16，17］等来对实验结果分析。

3.2 实验和结果

聚类分析的统计结果见图3、表2 和图4。

图3 两种方法在不同聚类个数下的精度Fig 3 Precision of the two methods under different number of clustering

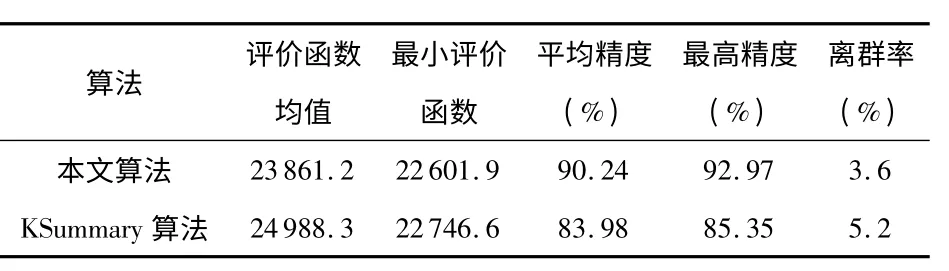
表1 实验结果统计Tab 1 Statistics of experimental results

表1 记录了实验过程的计算结果，结合图3 可以看到:本文算法得到的评价函数、平均评价函数都比原算法低，而最高精度和平均精度也优于原算法的处理结果。图3 也说明自适应多趟聚类算法可以找到在无线网络数据集上的最佳聚类个数，聚类的精度也达到了比较理想的数值。

图4 簇中对象的个数Fig 4 Number of objects in each cluster

图4 给出了聚类后的数据分布，给出了簇中数据对象的个数，容易发现第2，10 簇中数据比其他簇少很多，所以，这些对象就很大概率是要找的离群点，通过对这些对象的分析，可以定位到收集这些信息的无线传感器，进一步研究可以分析出该传感器某个节点的安全状况。

4 结束语

自适应多趟聚类分析方法相比传统KSummary 算法，从平均评价函数和平均精度都有更好的效果。自适应多趟聚类算法是将整个过程分为三趟聚类，三趟之间属于串行。与KSummary 算法相比，确实增加了一定的时间开销，但是在数量级与指数级上都没有增加，而且聚类的效果要好于原算法。

使用自适应多趟聚类算法，应用于传感器收集的无线网络数据中，离群点表现出来的信息与其他信息会有较大差异，这在本算法中会有明显的体现，实验结果也说明了这个问题。对聚类后找到的可疑离群点进行分析，定位到收集该信息的传感器，就能够知道该设备的节点是否处于安全的工作状态。

［1］ 王令剑，滕少华.聚类和时间序列分析在入侵检测中的应用［J］.计算机应用，2010，30(3):699-701.

［2］ Han Jianwei，Micheline Kamber，Pei Jian.数据挖掘概念与技术［M］.范 明，孟小峰，译.3 版.北京:机械工业出版社，2012.

［3］ Kanungo T，Mount D，Netanyahu N，et al.An efficient k-means clustering algorithm:Analysis and implementation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2002，24(7):881-992.

［4］ Dutta M，Kakoti A Mahanta，Arun Pujari K.QROCK:A quick version of the ROCK algorithm for clustering of categorical data［J］.Pattern Recognition Letters，2005，26(15):2364-2373.

［5］ 周水庚，周傲英，金 文，等.FDBSCAN:一种快速DBSCAN算法［J］.软件学报，2000，11(6):735-744.

［6］ 马华东，陶 丹.多媒体传感器网络及其研究进展［J］.软件学报，2006，17(9):2013-2028.

［7］ 陈 娟，张宏莉.无线传感网络安全研究综述［J］.哈尔滨工业大学学报，2011，43(7):90-95.

［8］ 蒋盛益，李 霞，郑 琪.数据挖掘原理与实践［M］.北京:电子工业出版社，2011.

［9］ 蒋盛益，李庆华.一种增强的K-Means 聚类算法［J］.计算机工程与科学，2006，28(11):56-59.

［10］马 力，焦李成，白 琳，等.自适应多克隆聚类算法及收敛性分析［J］.模式识别与人工智能，2008，21(1):72-83.

［11］汪 中，刘贵全，陈恩红.一种优化初始中心点的K-Means 算法［J］.模式识别与人工智能，2009，22(2):299-305.

［12］袁 方，周志勇，宋 鑫.初始聚类中心点优化的K-Means 算法［J］.计算机工程，2007，33(3):65-69.

［13］尹亚光，贵 广.无线传感器网络中的数据压缩技术研究［J］.计算机应用与软件，2010，27(7):1-4.

［14］张 军，杨子晨.多传感器数据采集系统中的数据融合研究［J］.传感器与微系统，2014，33(3):52-57.

［15］赵 伟，何丕廉，陈 霞，等.Web 日志挖掘中的数据预处理技术研究［J］.计算机应用，2003，23(5):62-67.

［16］Yosr N，Kaouther B S.Interpretability-based validity methods for clustering results evaluation［J］.Journal of Intelligent Information Systems，2012，39(1):109-139.

［17］Peter T，Jana H.Mathematical tools of cluster analysis［J］.Applied Mathematics，2003，4(5):814-816.

［18］古 平，刘海波，罗志恒.一种基于多重聚类的离群点检测算法［J］.计算机应用研究，2013，30(3):751-756.