一种GMI 传感器目标探测模型*

肖 晶，段修生，师菁菁

(1.军械工程学院，河北 石家庄050003;2.68129 部队，甘肃 兰州730060)

0 引 言

磁感应(magneto-induction，MI)自1992 年被日本名古屋大学的Mohri K 教授发现以来［1］就受到广泛关注。一方面，深入研究巨磁阻抗(giant magneto-impedance，GMI)效应的机理和模型，通过直流退火等工艺制得了阻抗变化倍数较高的非晶丝材料;另一方面，利用高阻抗变化倍数的非晶丝制成了GMI 传感器，设计了传感器的信号调理电路，并对其应用进行了探索［2～6］。日本、西班牙等国家在磁性标签和磁传感器领域已经实现了产品的商业化，国内相关研究主要是基于GMI 效应的电流传感器和弱磁场传感器，利用GMI 效应曲线的线性区实现了非接触测量。在军事领域，弱磁测量是地磁导航的关键技术之一，也是对潜艇、舰船、装甲车辆等目标无源探测的重要手段之一。北京理工大学的孙骥等人将GMI 效应应用于近感探测，使GMI 传感器在军事上受到了关注［7］。GMI 传感器的分辨率可达10－9T甚至更高，其体积小、能耗低、分辨精度高、响应速度快、宽适温湿压，且易于维护［8］，在目标的探测上具有巨大的优势。然而，军事目标探测中如果像电流传感器一样将GMI效应曲线的应用范围限制在较小的线性区域内，显然不能满足要求，也不利于发挥GMI 传感器灵敏度高的特点。

本文提出了一种GMI 传感器目标探测模型，引入曲线拟合与神经网络的思想，在保证测量精度的基础上拓展了探测范围。

1 GMI 传感器输出信号的特征提取和选择

GMI 传感器输出信号的提取应用较多的是包络检波，通过提取信号的幅值，建立与外加磁场的关系，多采用二极管包络检波电路［9］。这种方法简单且易实现，但只提取了信号的包络，忽略了输出信号的内在特征，可能影响传感器的性能。

为了便于研究GMI 传感器应用于坦克、潜艇等磁性目标的探测，在实验室环境下利用小磁体(直径1 cm、厚0.4cm、环状)模拟目标相对传感器运动，建立了由GMI传感器实验板、模拟磁性目标、同心圆距离指示板(相邻圆间隔0.5 cm)、台湾固纬(INSTEK)GFG—3015 函数信号发生器及泰克(Tektronix)TDS5104B 型数字示波器组成的实验系统，如图1(a)所示。由于纵向激励时非晶丝对与其轴向垂直方向的磁场不敏感［8］，因此，为了最大程度降低磁场对实验结果的影响，实验之前调整传感器的位置使示波器显示信号的幅值最小，此时可认为地磁场与传感器的轴向垂直，记为初始位置。

实验时，由信号发生器产生10 MHz 的正弦信号作为GMI 传感器的激励信号，让模拟磁性目标相对传感器做直线运动，输出信号由示波器采集并存储，图1(b)给出了几个典型位置的信号波形。

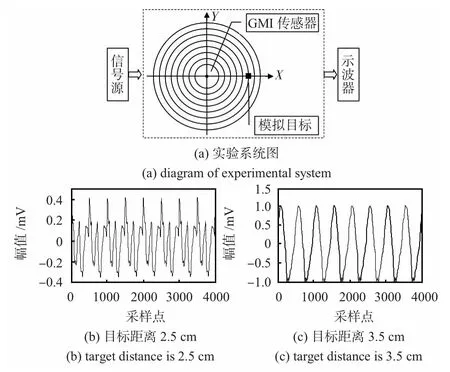
图1 实验系统图和两个典型位置的信号波形图Fig 1 Diagram of experimental system and signal waveforms at position of 2.5 cm and 3.5 cm

图1 (b)，(c)中信号幅值随着目标运动而变化，其脉内特征也变化明显。对给定方向的采集信号进行快速傅里叶变换(FFT)，观察其频谱变化，可知此时信号的频谱成分也在连续变化，且其谐波成分的变化非常显著。

任意一个实值函数，都可以写成式(1)傅里叶级数的形式

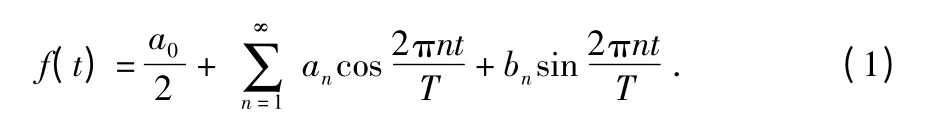
其中，an和bn为实频率分量的振幅，a0为直流分量的幅值的2 倍，T 为函数的周期。基于Matlab 对采集的数据进行离散FFT，变换后第n 点(表示为an+bni)对应的频率分量的频率、幅值与相位可以通过下式计算

其中，N 为采样的点数，Fs为采样频率，An为在fn频率下信号的幅值，A0为直流分量的幅值，pn为对应的相位。为了更清楚地表现各次谐波对信号波形的影响，按式(6)合成新的信号

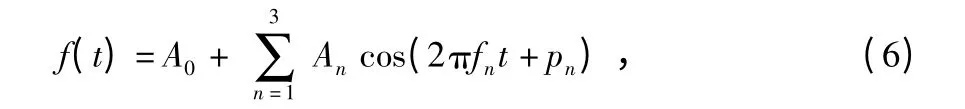
并与原始信号进行比较，结果见图2。

图2 是2 cm 位置的原信号和由不同频率成分按照式(6)合成的信号。可见，基频和二次谐波信息占据了主要部分，其次是三次谐波，加上四次谐波后的重构图像与三次谐波的结果基本相同(图中没有列出)，说明四次谐波和更高次的谐波对输出信号的影响很小。正是因为各次谐波的影响，造成了信号的正负幅值不对称，并且在某些距离范围(如图1 中2.5，3.5 cm 位置)出现了多个波峰的情况。为了改进单纯应用幅值特征的局限性，除了提取信号的电压幅值和功率信息外，还利用小波分析对波形的内部特征进行了提取。

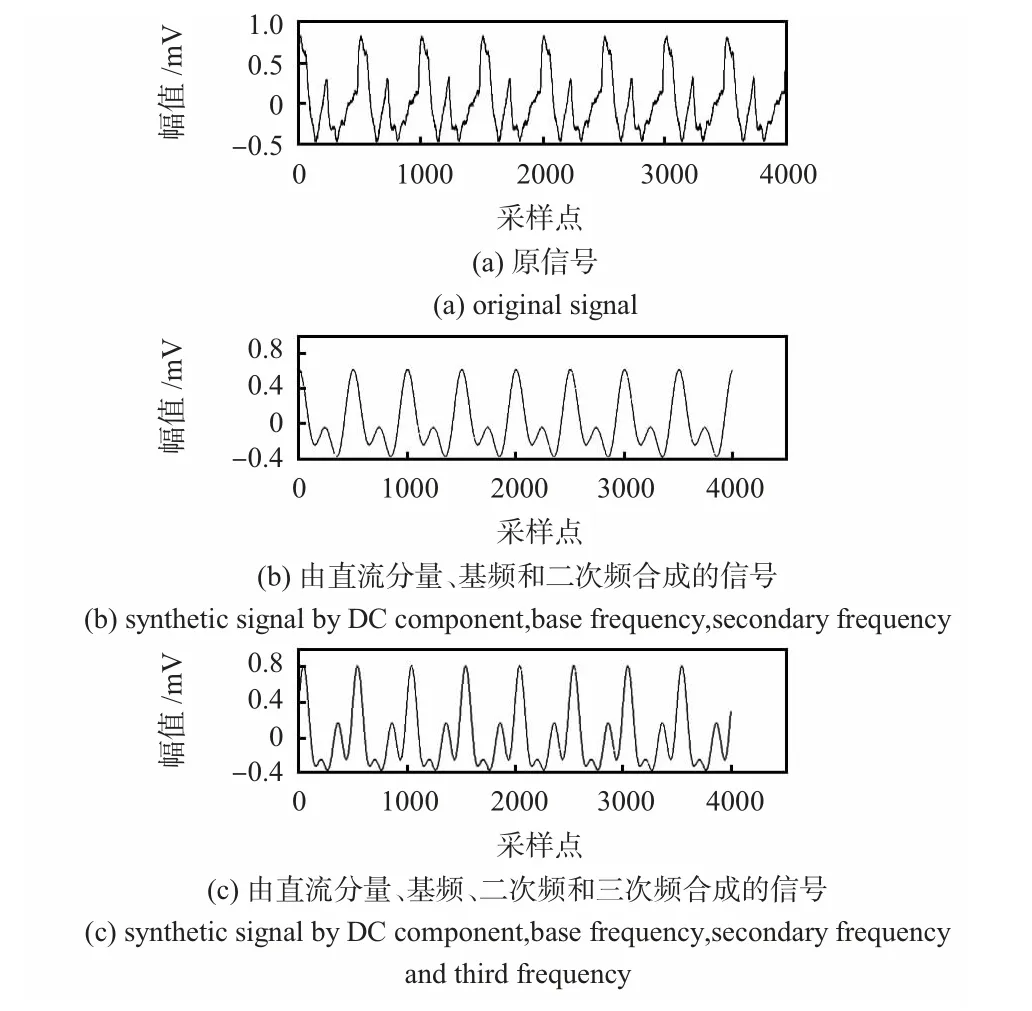
图2 2 cm 位置的信号FFT 与重构的结果Fig 2 FFT and reconstruction result of signal at position of 2 cm

先定义电压变化倍数Ur(i)和功率变化倍数Pr(i)两个特征量

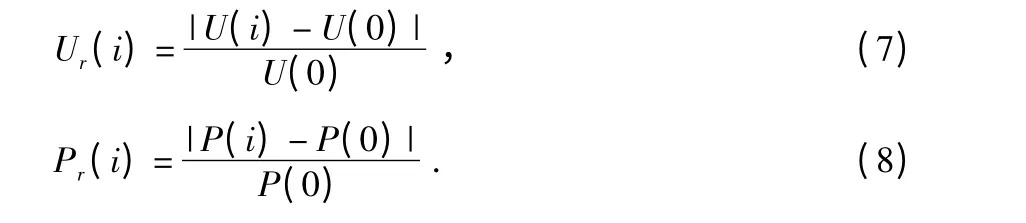
其中，U(i)和P(i)为目标在某一位置的电压幅值和功率，Ur(i)和Pr(i)为对应的电压幅值变化倍数和功率变化倍数，其算法如下:

1)采集初始状态和任一位置时传感器的输出信号;

2)通过过零点检测法提取N 个周期Num 个采样点的电压幅值A(i);

5)按定义计算电压幅值变化倍数Ur(i)与功率变化倍数Pr(i)。

图3 是所得的电压幅值和功率变化倍数曲线。

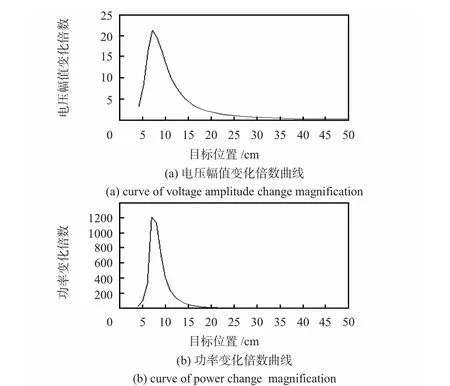
图3 电压幅值变化倍数曲线和功率变化倍数曲线Fig 3 Curves of voltage amplitude and power change magnification

两者的变化规律基本一致，都是先增大，经过一个最大值后逐渐衰减，最后趋于0。这与GMI 效应的变化规律一致，也在侧面验证了所取特征的有效性。两个变化倍数曲线都有一段近似直线的区域，一般的传感器多是基于该区域利用直线拟合模型设计的［10］。为了使设计的传感器能适应远距离的军事目标探测，本文引入非线性曲线拟合的方法，通过神经网络建立电压幅值与功率特征的融合模型，并以此标定传感器，达到拓展传感器探测范围的目的。

2 基于电压幅值与功率特征的传感器融合模型

2.1 基于电压幅值与功率特征的独立模型

首先单独以电压幅值变化倍数和功率变化倍数建立曲线模型，以其变化倍数的最大值为分界点将变化倍数曲线分为两段，建立各自的拟合模型，如图4。

图4(a)为电压幅值变化倍数拟合结果，可以表示为

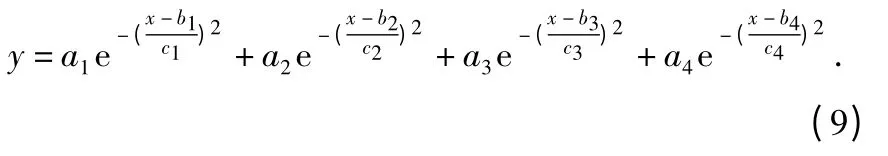
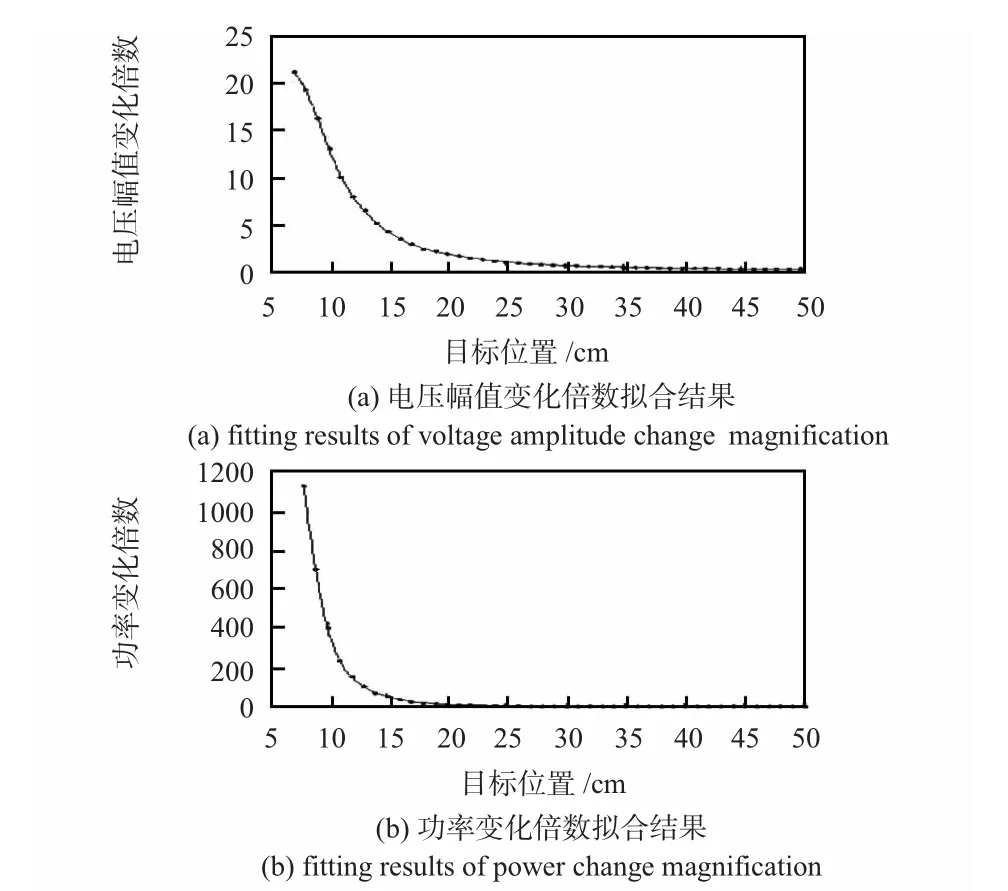
图4 电压幅值与功率变化倍数拟合结果Fig 4 Fitting result of voltage amplitude and power change magnification

其中，a1=2.564，b1=2.098，c1=2.072，a2=25.26，b2=－4.442，c2=8.652，a3=4.639×1013，b3=－979.2，c3=177，a4=0.6274，b4=11.35，c4=7.978。其误差的平方和为0.05，标准差为0.04。

图4(b)为功率变化倍数拟合结果，可以表示为

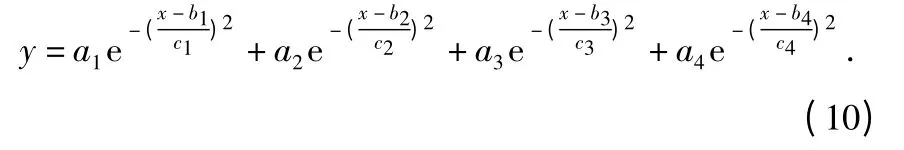
其中，a1=136 2，b1=5.544，c1=3.185，a2=1.309×1015，b2=－757.5，c2=135.1，a3=15.35，b3=12.37，c3=1.446，a4=2.712×105，b4=－37.1，c4=17.55。误差的平方和为3.785，标准差为0.349 4。

为了验证上述两个拟合模型，再采集几个位置的数据，通过求其电压幅值变化倍数与功率变化倍数预测目标相对传感器的位置，结果见表1。

由表可见，两者的预测结果各有特点，功率特征预测值在25 cm 之前有较好的精度，之后精度变低，因为此时功率的变化已经很小，用该段定位精度必然较低。电压幅值特征预测值在某些位置的预测精度较低，但可以相对精确地预测较远位置的目标。因此，需建立融合模型以克服二者单独应用时的缺点。

2.2 基于电压幅值、功率和小波分析的融合模型

建立基于电压幅值变化倍数与功率变化倍数的融合模型，只需在功率变化倍数模型预测精度不高时切换到电压幅值变化倍数模型。模型的切换通过BP 神经网络结合小波分解的系数实现，具体流程如图5 所示。

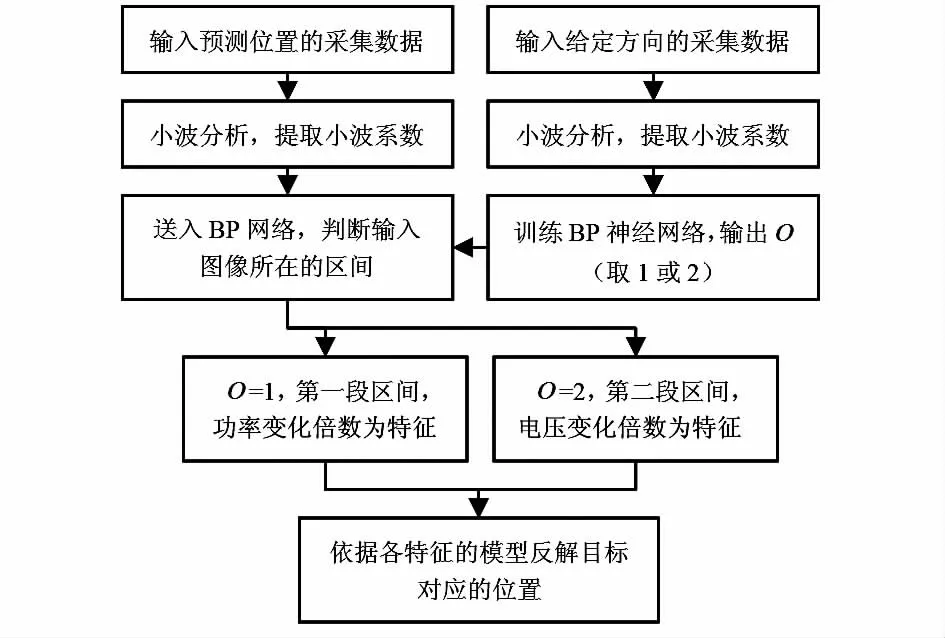
图5 融合模型的算法流程Fig 5 Algorithm flow chart of fusion model

先训练BP 神经网络，对给定方向的所有数据以“db5”小波进行4 层分解，得到小波分解的近似系数a4和细节系数d1，d2，d3，d4，经过多次实验发现只取近似系数a4和细节系数d1的能量值作为一个位置的特征量有较理想的预测结果，这样小波分解的结果使每个位置都对应一个含2 个能量值的特征向量，以该向量为神经网络的输入，并规定网络对位置25 cm 之前的信号输出为1，表示预测特征为功率变化倍数特征，该位置之后的输出为2，表示预测特征为电压幅值变化倍数特征，由此完成了模型的切换。在确定预测模型之后，就可以用曲线拟合模型求待预测的位置。

表1 的融合模型给出目标在8 个未知位置时的预测结果。由表可知，在39.5 cm 位置时该模型还可以保证很高的预测精度，并且相对误差控制在±1.33%之内，整体的预测效果优于独立使用电压幅值变化倍数和功率变化倍数特征预测的结果。位置43.3 cm 处精度不高主要是因为目标距离传感器较远，基本不能引起其交流阻抗的变化。

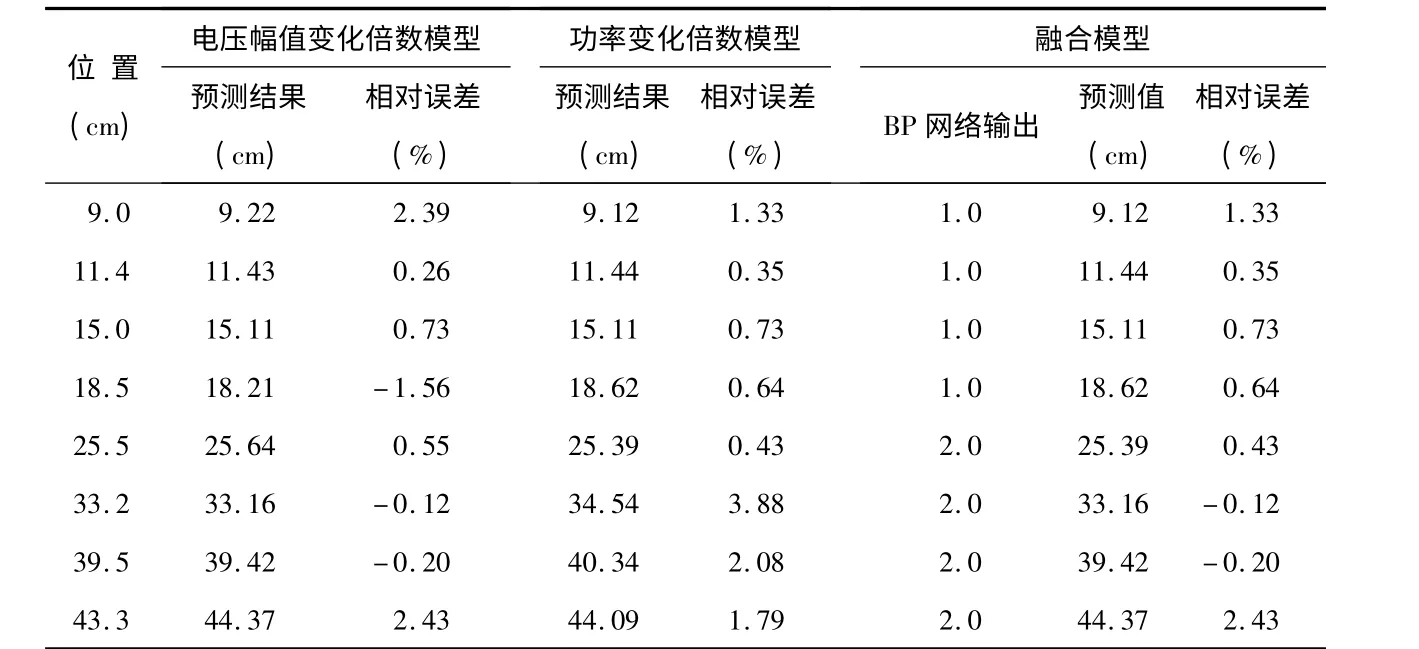
表1 融合模型的预测结果Tab 1 Prediction results of fusion model

3 结 论

军事应用中要求目标探测传感器在保证探测精度的前提下探测距离尽量远，本文提出的GMI 传感器目标探测模型对GMI 信号处理时的直线拟合方法进行了改进，并通过实验验证了该模型的有效性。该模型操作简便，易于实现，且定位精度高，在目标定位与跟踪领域具有很大的发展空间。但本文的研究只是实现任意位置目标探测的基础，要在军事目标探测中实现应用还需更深入的研究。

［1］ Mohri K，Kkohsawa T，Kawshima K，et al.Magneto-inductive effect(MI effect)in amorphous wires［J］.IEEE Transactions on Magnetics，1992，28(5):3150－3152.

［2］ Hoon Song，Duck-gun Park.Application of the magnetoimpedance to biosensors［J］.Journal of the Korean Physical Society，2012，61(10):1636－1640.

［3］ Wu Caipeng，Deng Jiahao，Sun Ji，et al.A design of linear AGMI sensor and its application for tank target detection［C］∥Proceedings of 9th International Conference on Electronic Measurement and Instruments，ICEMI 2009:Beijing，IEEE Computer Society，2009:21021－21026.

［4］ Yu Geliang，Bu Xiongzhu，Yang Bo，et al.Differential-type GMI magnetic sensor based on longitudinal excitation［J］.IEEE Sensors Journal，2011，11(10):2273－2278.

［5］ Han Bing，Zhang Tao，Huang Dongyan，et al.Giant magnetoimpedance current sensor with spiral structure double-probe［J］.IEEE Transactions on Magnetics，2009，45(4):1999－2002.

［6］ 柴秀丽，张延宇.巨磁阻抗磁传感器研究进展［J］.传感器与微系统，2011，30(12):11－13.

［7］ 孙 骥，邓甲昊，高 珍，等.基于巨磁阻抗效应的新型微磁近感探测技术［J］.仪表技术与传感器，2009(4):93－96.

［8］ 柴秀丽，曾德长，刘桂雄，等.非晶纳米晶带材巨磁阻抗磁传感器特性分析［J］.传感器与微系统，2008，27(9):63－65.

［9］ 于葛亮，雄 洙，史晓君，等.基于纵向激励的铁基非晶带弱磁传感器研究［J］.南京理工大学学报，2011，35(3):338－342.

［10］Tarun Das，Pallab Banerji，Banerji Pallab.An embedded magnetic field sensing device utilizing giant magnetoimpedance(GMI)effect［C］∥Proceedings of the International Conference on Sensing Technology，Kolkata，ICST 2012，Washington:IEEE Computer Society，2012:102－107.