脉冲磁场传感器频率特性分析与拓宽频带方法

贺 海，马少杰，史云雷

(南京理工大学 机械工程学院，江苏 南京210094)

0 引 言

长期以来，电磁脉冲对电子、电力系统构成的巨大威胁已引起人们的高度重视。电磁脉冲是一种瞬变的电磁现象，除了人们熟知的雷电会产生电磁脉冲以外，静电放电和大功率电子、电气开关也会产生电磁脉冲［1，2］。尤其是核爆炸产生的电磁脉冲，峰值场强极高，上升时间极短［3］。电磁脉冲频率范围比较广，被测信号包含各种频率成分，而且在空间各处的幅值不同，其脉冲的上升沿分布从μs 级到ns 级，产生的瞬变电磁场幅值范围大、频带宽。

本文针对线圈型磁场传感器，分析了其测量原理及其频率特性，提出了拓宽传感器工作频带的方法，在此基础上，设计并测试一种测量宽频带磁场的线圈型磁场传感器。

1 线圈型磁场传感器的测量原理

线圈型磁场传感器以法拉第电磁感应定律为基础，与普通电子类传感器相比，适用范围广，可以实现直流磁场、交流磁场、脉冲磁场的测量，可测磁场强度和频率范围大。磁场传感器结构如图1 所示，为了消除电场对线圈的影响，通常采用顶部带间隙的环状屏蔽套，屏蔽套可以采用任何非磁性的良导体［4］。其工作原理是外导体在间隙处感应出开路电压，这一电压经过两侧半圆的屏蔽层传至负载端，形成平衡的差动输出。线圈与电阻RL并联，通过BNC 电缆接头将电阻RL两端的电压输出。整个环是屏蔽对称的结构，抗干扰能力得到了增强。

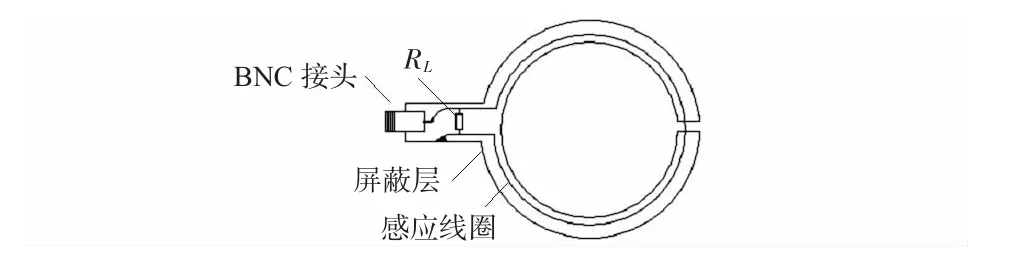
图1 磁场传感器示意图Fig 1 Schematic diagram of magnetic field sensor

磁场传感器的等效电路如图2 所示。图中，R0为磁场传感器的自电阻，C0为线圈的自身电容，L0为线圈自身电感，RL为磁场传感器的负载电阻。根据电磁感应定律，当把截面积为A、绕有匝数为N 的探测线圈置于磁感应强度为B 的随时间变化的被测磁场中时，在探测线圈中会产生感应电动势。

假设磁场强度B 与测量线圈平面相互垂直，由此得到的感应电动势emf为

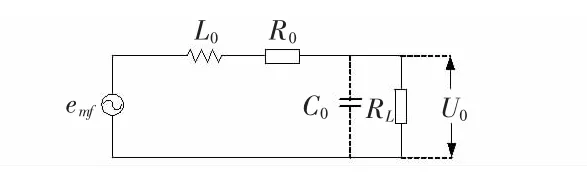
图2 磁场传感器的等效电路图Fig 2 Equivalent circuit diagram of magnetic field sensor

经傅里叶变换得到

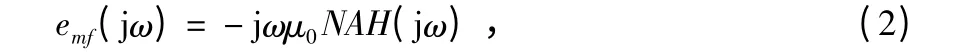
式中 Φ 为穿过线圈的磁通量，H 为磁场强度。

R0相对与线圈的感抗ωL0来说可以忽略不计，由此得到探头的输出电压为

式中 ω 为磁场的角频率;μ0=4π×10－7H/m 为自由空间的磁导率。

多匝线圈的电感计算公式为［5］

式中 a 为线圈的半径，b 为绕制探测线圈用的导线的半径。

2 负载电阻RL 对测量频率范围的影响

探测线圈的输出电压与待测场的频率和负载电阻值有一定的关系。要使磁场传感器的频率响应在所有希望的频率范围内比较平滑，可以通过调节传感器终端的负载电阻来达到所要求的频率范围。对测量频率范围的影响具体分析，实际上自积分电阻RL总并联有一定的杂散电容C0(包括线圈的分布电容、间隙电容)。

根据克希荷夫电压定律得到电路微分方程为

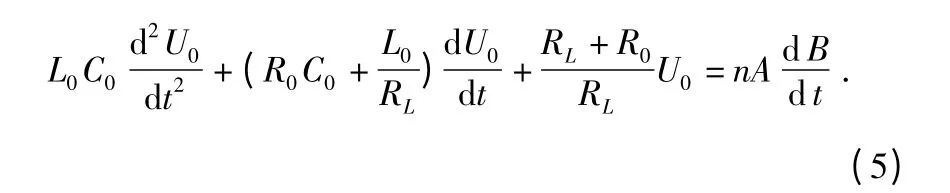
2.1 忽略C0 影响

磁场传感器中C0很小，即C0=0，将等效电路简化为一阶电路，即

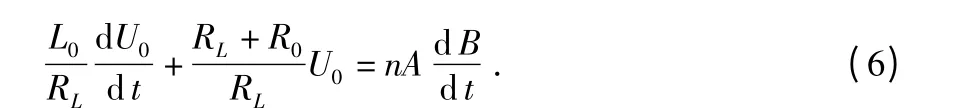
当ω 很小时，满足ωL0≪RL+R0，输出电压为

即输出电压U0与所测磁感应强度B 的微分呈正比，此时，在频域中可以认为探头的输出电压与外界磁场的频率呈正比，在时域中表现为输出电压与待测磁场的时间导数呈正比，具有这种特性的磁场传感器被称为 ˙B(B－dot)磁场传感器。

当ω 很大时，满足ωL0≫RL+R0，输出电压为

在这种条件下，RL与L0构成一个RL积分器，使传感器实现了自积分，输出U0与磁感应强度B 呈正比，测得信号直接反映磁感应强度，此时传感器的输出电压就与待测磁场的频率无关，而且与场强值B(H)呈正比，具有这种特性的磁场传感器被称为B(H)磁场传感器。随着磁场频率的增加，线圈型磁场传感器的工作方式由 ˙B(B－dot)传感器向B(H)传感器转换，工作方式发生转换的磁场频率称为转换频率fC［6］

2.2 考虑C0 影响

当考虑C0影响时，等效电路图所示电路的微分方程为

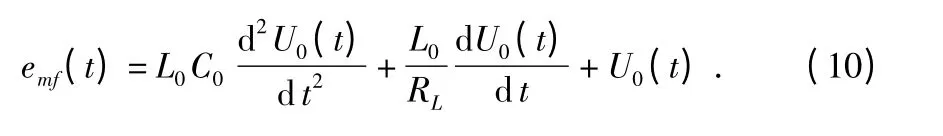
将上式进行拉普拉斯变换，可以得出传递函数为

由此可以得到探测线圈的归一化传递函数为

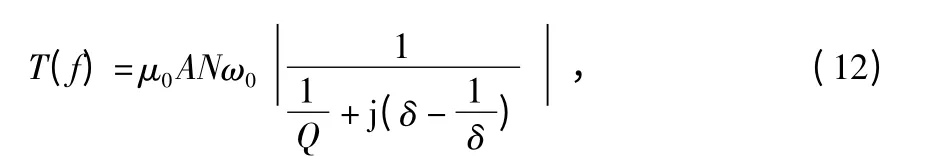
式中 线圈的自谐振频率为ω0，探测线圈的品质因数为

由归一化曲线函数可以得到线圈归一化曲线频率上－3 dB截止频率分别为

上截止频率

下截止频率

带宽为

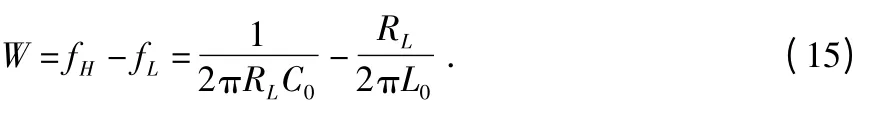
探测线圈要获得较大的带宽，应使fH尽量大，而fL应尽可能小，即，使L0尽可能大，RL，C0尽可能小。

3 灵敏度分析

传感器输出电压U0与测量线圈的面积A 呈正比，故线圈面积越大，测量的灵敏度就越高，但这种探测线圈测量的是线圈面积内的平均磁场强度，所以，线圈面积越大，测量结果偏离中心点场强值的误差就越大。

传感器的灵敏度就是传感器输出信号与被测信号的比例，磁场传感器输出电压为

由此得到传感器的灵敏度S 为

由式(17)可知，增大a(即探测线圈面积)，RL，b，减小N 可提高S。但是减小N、增大RL将减小带宽W，实际设计时应综合考虑参数的选择。

4 仿真与实验研究

根据传感器的灵敏度要求，取线圈直径a=65 mm，导线半径b=0.5 mm，线圈匝数为1 匝。根据式(4)算得自感L0=0.21 μH。

根据传递函数，通过改变探测线圈的品质因素，也就是改变与探测线圈并联的负载电阻RL的值，就可以使上述传递函数在所考虑的频率范围内有比较平滑的响应，通过仿真可以得到不同电阻RH时的归一化频率特性图(图3)。

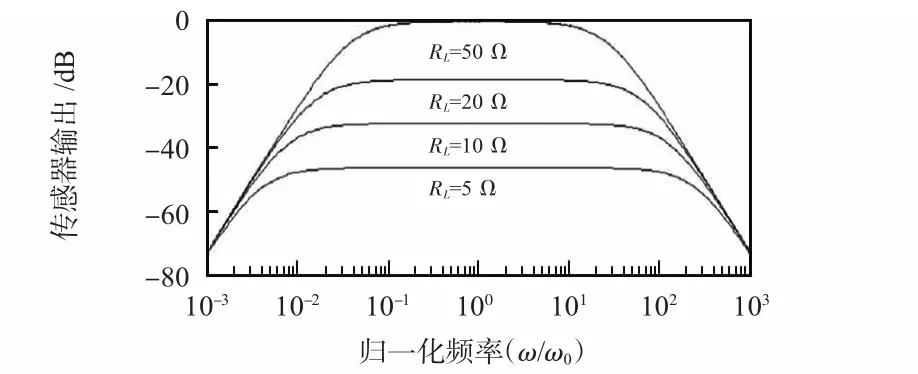
图3 探测线圈传递函数归一化频率特性Fig 3 Normalized frequency characteristic of detecting coil transfer function

根据式(13)、式(14)可以计算出与探测线圈相连的负载电阻RL不同的阻值对应的探测线圈上、下截止频率fH，fL的值以及品质因素Q 的值，如表1 所示。

表1 探测线圈频率特性参数Tab 1 Frequency characteristics parameters of detecting coil

由探测线圈传递函数归一化频率特性曲线可以看出，在只改变RL值的情况下，随着RL值的减小，探测线圈的有效带宽值越大，品质因素Q 的值越小，即其获得平滑响应的频率范围越大。随着RL的值增大，探测线圈的输出值越大。RL值的取值还受到探测线圈的灵敏度和转折频率的限制，图4 为磁场传感器RL=10 Ω 时，磁场传感器的传递函数曲线，fC=7 MHz;图5 是在100 kHz 频率下的响应曲线和对其进行系数处理后积分得到的磁感应强度曲线;图6是在10 MHz 频率下的响应曲线。为了避免测得的磁场信号紊乱，所设计的探测线圈的转折频率不能处于所测磁场频率的范围内。

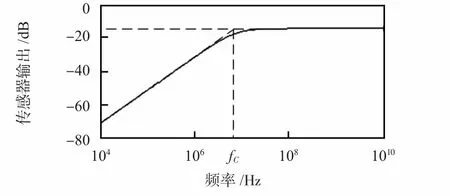
图4 磁场传感器的传递函数曲线Fig 4 Transfer function curve of magnetic field sensor

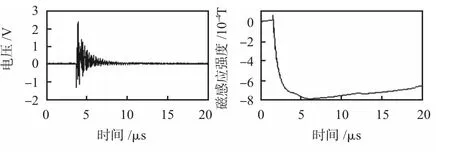
图5 100 kHz 频率下脉冲响应曲线及其积分曲线Fig 5 Pulse response curve and its integral curve at frequency of 100 kHz

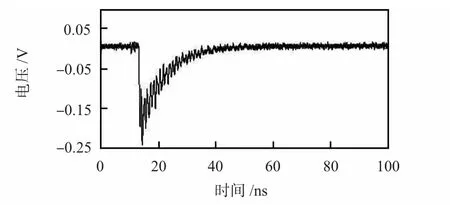
图6 10 MHz 脉冲响应曲线Fig 6 Pulse response curve at frequency of 10 MHz

5 结 论

本文提出了一种线圈型磁场传感器和拓宽频带的方法，仿真得出通过改变线圈的负载电阻，可以改变磁场探测线圈的频率特性，拓宽频带;改善线圈的设计参数，可以改变线圈的固有频率，选择合适的负载电阻RL，可以增大探测线圈的有效频率响应范围。在选择合适的RL时，还需要考虑线圈的灵敏度和转折频率，以选择探测线圈工作时是微分环还是积分环。实验表明:通过这些改善方法，可以拓宽磁场探测线圈的频率响应范围，增大线圈的工作频带，使其具有很好的暂态响应，提高系统的测量性能。

［1］ 王泽忠，李云伟，卢斌先，等.变电站电磁脉冲耦合倾斜二次电缆数值分析［J］.高电压技术，2007，33(7):98－101.

［2］ 田世杰.变电站开关操作瞬态电磁环境研究［J］.吉林电力，2011，39(2):20－22.

［3］ Longmire C L.On the electromagnetic pulse produced by nuclear explosions［J］.IEEE Transaction on Antennas and Propagation，1978，20(1):3－13.

［4］ 李 雪，刘泰康，姜 云.电磁屏蔽技术分析［J］.电子工艺技术，2007，28(1):49－51.

［5］ 刘修泉，曾昭瑞，黄 平.空心线圈电感的计算与实验分析［J］.工程设计学报，2008，15(2):149－153.

［6］ 丁 炜，彭 涛，辜承林.脉冲强磁场探测系统的基本实现［J］.核电子学与探测技术，2006，26(3):998－1000.