基于熔融纺丝PAN原丝的数值模拟研究

刘婷婷，甘学辉，纪俊洋

(东华大学机械工程学院，上海201620)

高性能聚丙烯腈(PAN)原丝是制备PAN基碳纤维最核心的技术，也是制备高性能碳纤维的关键。PAN原丝质量是制约碳纤维工业发展的瓶颈问题［1］。目前，人们采用各种各样的方法提高PAN原丝的质量和碳纤维的力学性能，并把碳纤维列入21世纪的尖端材料［2］。

由于丙烯腈聚合物氰基之间因偶极作用而产生的链的僵硬和偶合引起的熔点高(317℃)，在加热时还未熔融就已分解，因此只能用溶液纺丝生产PAN纤维。如果PAN纤维能够实现熔融纺丝，不仅节约溶剂消耗，而且省去了溶剂回收工艺和设备及水洗过程，可以大大降低生产成本，消除由于使用溶剂引起的严重环境污染问题。

多年来，一些科研机构一直致力于PAN熔融纺丝技术的研究。1952年，C.D.Coxe首先报道了在PAN类共聚物中增添少量的水可以将其熔点降至熔纺要求的温度［3］。近20年来，国外许多生产公司对PAN纤维的熔融纺丝进行了大量的研究，如有美国的氰胺公司、杜邦公司、英国的BP Chemical公司、日本的三菱人造丝公司、爱克斯纶公司、旭化成公司、东邦贝斯伦公司等先后开展了熔融纺丝法制备PAN纤维的研究开发，取得了一定的研究进展，但是至今仍没有实现工业化生产。

碳纤维的加工是一项成本很高的产业，无法通过大量的实验优化原丝的性能。由此，数值仿真模拟技术是一个不可替代的环节，通过对熔融纺丝制备PAN原丝的模拟，可随时优化其工艺参数与力学模型，对我国研究PAN纤维的熔融纺丝新工艺，对低成本制备PAN碳纤维原丝具有重要意义。

1 熔融纺丝制备PAN原丝的数学模型

1.1 熔融纺丝技术

从图1可见，纺丝熔体由喷丝孔挤出时，恒定的温度(T0)、流量与喷丝孔的直径(d0)及材料的密度一起决定了挤出速度(V0)。卷绕装置距喷丝头的距离为L，纤维有恒定的卷绕速度，与纺织纤维的平均直径有关。沿纺程(x)即从挤出(x为0)到卷绕(x为L)之间，流体细流经变形、冷却、固化成具有超分子结构的纤维。图1中V为丝条运行速度，T为丝条的温度，d为纤维直径，TL，VL，dL分别为进入卷绕时丝条的温度、速度和直径。熔融纺丝的主要工艺参数为挤出温度、聚合物通过喷丝板各孔的质量流速、卷绕速度、纺程的冷却条件、喷丝孔形状、尺寸及间距和纺程长度［4］。这些参数之间相互关联，例如纺程长度常常受纺程上冷却效率的控制，高效的冷却可以缩短纺程;冷却空气的速度、温度及分布对丝条的冷却有很大的影响。

图1 熔融纺丝熔体挤出过程Fig.1 Melt extrusion process during melt spinning

1.2 制备PAN初生纤维及原丝

PAN粉末:相对分子质量50 000～150 000，南京斯泰宝贸易有限公司产。采用日本进口单螺杆挤出机对增塑PAN粉末进行熔融纺丝，经过卷绕装置、水浴拉伸装置制得PAN原丝。在纺丝温度200 ℃，微孔流量1.25 ×10－8m3/s，拉伸倍数2倍的条件下，1#，2#，3#试样的卷绕速度分别为 30，100，200 m/min。其纺丝工艺流程和纺丝工艺参数分别见图2和表1。

图2 PAN熔融纺丝工艺流程Fig.2 Flow diagram of PAN melt spinning process

表1 PAN纺丝工艺参数Tab.1 PAN spinning process parameters

1.3 熔融纺丝基本数学方程

高聚物熔体有很高的黏度，流动时的雷诺数较小，因此可以假定高聚物熔体的流动为不可压缩的稳定层流，另外高聚物熔体的惯性力和质量力相对于粘性力相当小，因此可忽略不计。在上述假设条件下，在流动域上，高聚物熔体满足3个守恒方程，即质量守恒方程、动量守恒方程和能量守恒方程［5－8］。

连续性方程:

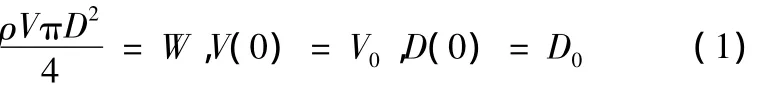
动量守恒方程:

能量守恒方程:

本构方程:

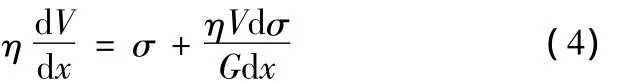
式中:ρ为熔体密度;D为丝条的横截面直径;W为泵供量;F为丝条沿纺丝线的轴向张力;g为重力加速度;τf为丝条与空气摩擦引起的剪切应力;h为传热系数;T为丝条的温度;Cp为比热;η为拉伸黏度;G为弹性系数;σ为丝条单位截面上的应力。

2 数值模拟研究

基于CFD的有限元方法求解聚合物成形问题应用非常广泛［9－11］，应用该方法可对速度场、温度场等参数进行计算机可视化研究。Polyflow软件可以对聚合物成型加工过程进行模拟，用来求解高聚物熔体流动过程中的温度场、速度场、压力场、剪切应力场、黏度、流线的分布，可以动态、在线实时、定量地反映熔体的流动过程，为优化成型设备的设计提供科学依据。

2.1 微分粘弹模型

Phan-Thien-Tanner(PTT)是微分粘弹性模型中最实际的模型之一，它可以表现高剪切速率流体的剪切变稀和存在法向应力差的流变行为。

2.2 边界条件

微孔壁面:无滑移流动，即

式中:Vn为法向速度;Vs为切向速度。

熔体入口(Inflow)流量(Q)为 1.25×10－8m3/s。

熔体出口(Outflow)V为30 m/min，不考虑牵引速度影响，即

式中:fn为挤出端自由面的法向力;fs为挤出端自由面的切向力。

迭代方法:为了减少计算量，压力和应力采用线性迭代，黏度采用Picard迭代，速度采用Minielement迭代。

2.3 模拟参数

模拟的模型和材料参数见图3和表2。工艺参数为:纺丝温度200℃，微孔流量1.25×10－8m3/s，卷绕速度30 m/min，无拉伸。

图3 数值模型Fig.3 Numerical model

表2 PAN材料参数Tab.2 PAN material parameters

3 结果与讨论

3.1 数值模拟结果分析

3.1.1 纤维直径模拟

通过数值模拟从理论上预测了纺丝过程中丝条沿纺程上的直径变化，并同实验测得的数据进行了比较，见图4。从图4可知，在距喷丝板0～10 cm处纤维直径急剧缩小，10～20 cm处开始缓慢减小，之后趋于稳定，说明纤维趋于固化完全。此外，模拟数据和实验数据能够较好地拟合，说明本数值模拟采用的模型可以较准确地模拟PAN熔融纺丝过程直径变化。

图4 沿纺程上的丝条直径变化曲线Fig.4 Filament diameter change along spinning path

3.1.2 速度场模拟

在数值模拟中，在纺程上各点卷绕速度值称为拉伸速率，则拉伸速率的收敛值即纺丝卷绕速度。本模拟比较了纺丝卷绕速度为30 m/min时，纤维中心和纤维表面的速度变化。从图5可见，纤维表面和纤维中心速度分布几乎完全重合，这表明在纤维横向断面上拉伸速率是均匀的，拉伸成形受力均匀。模拟与实验计算结果进行对比，结果表明，数值模拟预测的拉伸速率与实际的纺丝速度变化规律十分接近，说明本数值模拟采用的模型可以较准确地模拟PAN熔融纺丝过程速率变化。此外，速度变化较均匀，对纤维成型有利，避免纤维粗细不均，在后期牵伸过程中断裂。

图5 沿纺程上的纺丝速度变化曲线Fig.5 Spinning velocity change along spinning path

3.1.3 温度场模拟

在数值模拟中，温度分布的收敛值即纤维完全固化温度。建立2D轴对称的模拟模型不仅可以显示纤维表面与外界冷却气体之间的对流过程，而且还能预测纤维径向的温度梯度。实验中仅能测量纤维表面的温度分布，数值模拟计算预测的纤维温度分布与实验值比较见图6。从图6可以看出，纤维中心温度比纤维表面一直要高，尤其是离喷丝孔不远处(x为2～15 cm)，纤维中心与纤维表面温差一直很大，之后温差变小。这是由于在熔体纺丝过程中，纤维不仅与冷却气体进行对流传热，而且存在结晶放热，这两种相反的传热机制致使纤维中心温度高于纤维表面温度。本文数值模拟温差值最大15℃属正常范畴。

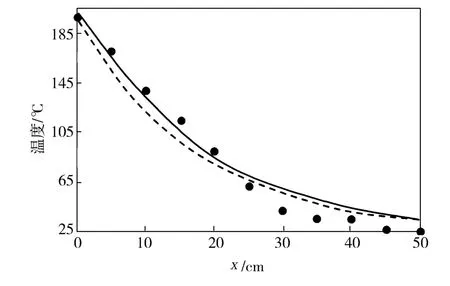
图6 沿纺程上的纤维温度Fig.6 Filament temperature along spinning path

纤维表面和纤维中心的温度差如果太大，不仅影响结晶度，纤维中心和表面的晶粒尺寸也会相差很大，进而造成纤维粗细不均，影响纤维的拉伸性能。由于缓慢降温可以提高结晶率，所以纺丝速度不能一味增大。在一定速度范围内，纺丝卷绕速度越低，纤维内外温差越小，纤维整体结晶越均匀，结晶度也会越大，纤维拉伸强度更高。

3.2 PAN原丝力学性能

从表3可以看出，卷绕速度最大的3#试样，其直径最小为0.029 mm，断裂强度最高为8.92 cN/dtex，断裂伸长率也达到了13.88%。按照日本三菱人造丝公司的专利说明［12］，适合高性能碳纤维的原丝拉伸强度不小于7.0 cN/dtex，原丝质量达到了此标准。

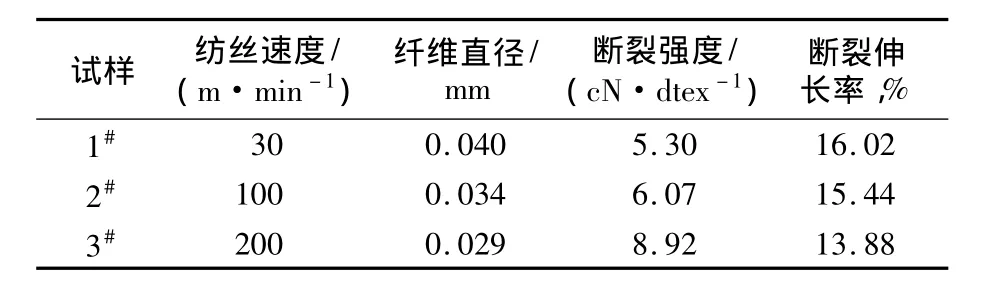
表3 不同纺丝速度下PAN原丝力学性能Tab.3 Mechanical properties of PAN precursor at different spinning velocity

4 结论

a.利用数值模拟从理论上预测了纤维的直径变化、拉伸速率分布、温度分布的规律。在距喷丝板0～10 cm处纤维直径急剧缩小，10～20 cm处开始缓慢减小，之后趋于稳定，表明纤维趋于固化完全;纤维表面和纤维中心速度分布几乎完全重合，表明在纤维横向断面上拉伸速率是均匀的，拉伸成形受力均匀;纤维中心温度比表面一直要高，尤其是离喷丝板不远处(x为2～15 cm)，纤维中心与纤维表面温差一直很大，之后温差变小最终趋于0℃。

b.本数值模拟采用的模型可以较准确地模拟PAN熔融纺丝过程纤维直径、拉伸速率、温度的变化过程。

c.实验制备出的PAN原丝，其力学性能满足高性能碳纤维原丝的强度要求。

［1］ 张旺玺.聚丙烯腈基碳纤维［M］.上海:东华大学出版社，2005:1－10.

［2］ 潘鼎，陈惠芳，秦琪生，等.高纯度PAN基碳纤维及其原丝的研制［J］.中国纺织大学学报，1993，19(6):1 －9.

［3］ Coxe C D.Preparation of shaped articles from acrylonitrile polymers:US，2585444［P］.1952 －02 －12.

［4］ 赵瑞辉，王朝生.细旦中空涤纶-PET-短纤维熔融纺丝动力学研究及应用［D］.上海:东华大学，2009.

［5］ Mitsoulis E，Georgios G C，Kountouriotis Z .A study of various factors affecting Newtonian extrudate swell［J］.Comput Fluids，2012，57(4):195 －207.

［6］ 吕静，陈晋南，胡冬冬.流率和牵引速度对两种聚合物熔体共挤出影响的数值研究［J］.北京理工大学学报，2003，23(6):781－784.

［7］ 张敏，孙胜，贾玉玺，等.聚合物共挤出的挤出胀大有限元分析［J］.高分子材料科学与工程，2006，22(5):36－39.

［8］ Mompean G，Thais L，Tome M F，et al.Numerical prediction of three-dimensional time-dependent viscoelastic extrudate swell using differential and algebraic models［J］.Comput Fluids，2011，44(1):68 －78.

［9］ 马文琦，孙红镱.塑料成型模拟软件技术基础与应用［M］.北京:中国铁道出版社，2006:1－15.

［10］徐佩弦.高聚物流变学及其应用［M］.北京:化学工业出版社，2003:1－20.

［11］陈晋南，胡冬冬，彭炯.Polyflow软件包在聚合物挤出成型中的应用［J］.世界科技研究与发展，2002(1):28 －34.

［12］ Okuya T，Hamada M，Kageyama Y，et al.Acrylonitrile-based precursor fiber for carbon fiber and method for production thereof:EP，1130140A［P］.2001 －05 －09.