纺丝组件中多孔介质对PA6熔体流动性能的影响

甘丽华，李 健，唐兵兵，韩 娜，李 鑫

(1.天津工业大学改性与功能纤维天津市重点实验室，天津300387;2.中国纺织科学研究院生物源纤维制造技术国家重点实验室，北京100025)

纺丝组件是纺丝技术中的关键设备，组件内的金属砂、金属网等在熔体过滤、均化、增压等方面起着关键作用，对微细旦、多孔数纤维均匀性和纺丝过程稳定性的影响尤为重要。金属砂、金属网本质上是多孔介质。

对多孔介质中流体流动的研究，多用平行管束模型表征多孔介质中非牛顿流体的渗流问题。修正后的Darcy方程能够较好描述非牛顿流体流动阻力特性，但用于粘弹性流体时，出现较大的偏差，这主要是由于没有考虑到流道直径的变化，只计算了纯剪切流动，忽视了拉伸流动和瞬态粘弹行为的作用。聚合物熔体即使在流速很低的情况下也表现出粘弹性，对熔体在多孔介质中的流动性能有着重要影响，需要在流动方程中添加惯性损耗来描述由弹性作用引起的压力损失［1］。

作者以聚己内酰胺(PA6)熔体为研究对象，采用增加了金属过滤砂的毛细管流变仪，研究了多孔介质目数和表观流速对PA6熔体流动阻力的影响规律，对于新型纺丝组件的开发、高品质和超细旦PA6纤维的开发具有指导作用。

1 实验

1.1 原料及仪器

PA6切片:相对黏度为2.54，纤维级，锦江科技有限公司产，经115℃真空干燥10 h用于测试;不同过滤精度金属砂:其目数相对应的平均粒径(D)如表1所示，亿帝化纤科技有限公司产。

表1 不同目数滤砂对应的粒径Tab.1 Particle size of filter sand with different mesh

Rheograph 25型毛细管流变仪:德国Gottfertt公司产;模拟组件:砂腔直径(d)为15 mm，高度(h)为35 mm，喷丝板及分配板孔径均为1 mm，自制模拟组件见图1。

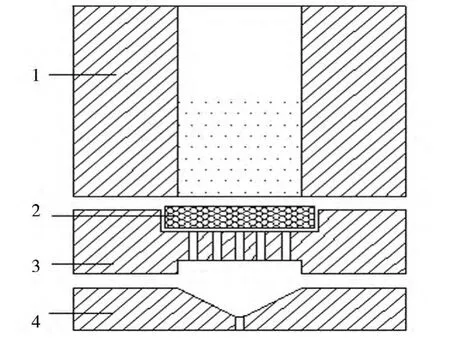
图1 模拟组件结构示意Fig.1 Simulation schematic diagram of spinning pack

1.2 实验方法及数据处理

采用毛细管流变仪及配套模拟组件，实验流速为0.03 ～0.90 mm/s，5 种不同精度过滤砂实验温度为265℃，其中选用60～80目过滤砂分别在255，265，275 ℃熔融5 min后，开始实验。

利用模拟组件入口处的压力传感器，测定熔体流动时的压力。未装填金属砂的不同流速下熔体压力值为P1，在不同过滤精度金属砂的实验中控制装砂高度为10 mm，压力传感器测得不同流速下的压力值为P2，可以通过压力差来表示熔体在通过多孔介质流动时所产生的压力增加值(△P)，即:

根据 Forchheimer方程［2］有:

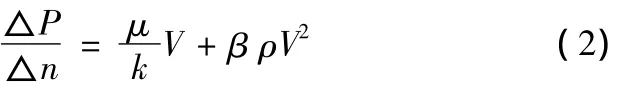
惯性损耗所占比例(W)定义为非Darcy项在总△P中所占的百分比。

2 结果与讨论

2.1 △P与V的关系

从图2可看出:熔体表观流速为0.03～0.90 mm/s时，PA6熔体流动△P随V增加而增大;不论金属砂粒径大小，随着V的增加，PA6熔体在多孔介质中流动所产生的△P都增大，这与牛顿流体和非牛顿流体中的一般粘性流体的流动规律是相符的［3］。同时，PA6为粘弹性流体，除具有粘性外，还具有弹性，这是由PA6分子的多分散性决定的。在通过多孔介质微细通道，尤其是孔径复杂变化的微细通道时，PA6分子及其链段在拉伸流场中发生取向，此时所需能量转化储存为弹性能，从△P的角度则体现为弹性损耗。并且这种弹性损耗会随着V的增加，即拉伸流场的增强而逐渐增加，最终也导致 △P随V的增加而增加［4－5］。在同一V下，过滤精度高的多孔介质比过滤精度低的介质产生的△P高，这主要因为过滤精度高的介质孔隙直径相对较小，空隙弯曲，迂曲度大，熔体在其孔隙中流动时，不但与孔道表面产生很强相互作用力，而且运动轨迹延长，介质对熔体流动的阻碍作用大，相应的△P较大。

图2 不同过滤介质下PA6的△P与V的关系Fig.2 Relationship between △P and V of PA6 through different filter media

图2中实线是按照Forchheimer方程拟合的曲线。1#，2#，3#，4#，5#过滤金属砂的拟合方程及相关系数(R)分别如下:

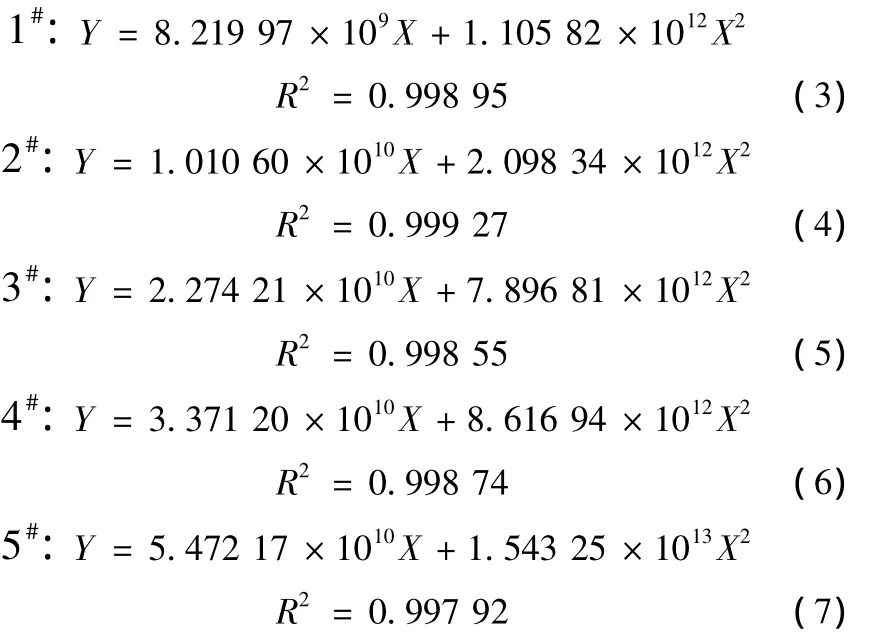
由拟合结果可以看出，各曲线拟合的R2均大于0.997，Forchheimer方程可以较好地描述PA6熔体在多孔介质中流动时△P与V的关系。

2.2 D对β的影响

根据实验所测数据△P与V关系，根据式(2)，即Forchheimer方程拟合，取ρ为970 kg/m3，△n为0.01 m，μ 为138 Pa·s，可求得1/k，β。

从图3可以看出，随着多孔介质D的减小，1/k及β均增大，并且β较1/k大2个数量级，这主要因为当多孔介质粒径减小时，相互之间堆积越紧密，给熔体流动留下的自由空隙减小，此时熔体分子通过多孔介质时受到的拉伸收敛作用越强，从而使得β增加;并且金属砂粒径越小，比表面积越大，与熔体相互作用面积越大，由粘性产生阻力越大，从而使1/k随粒径的减小而增加，如式(2)所示。说明当熔体通过多孔介质的V足够大时，△P中由弹性效应所引起的惯性损耗比粘性所引起的粘性损耗所占比例增加幅度更为显著，导致惯性损耗随着V的增加在总的△P所占比例增加。

图3 1/k及β与D的关系Fig.3 Relationship between 1/k or β and D

2.3 温度对β的影响

从图4可知，随着温度的升高，1/k与β都减小。并且 β的减小幅度比1/k的减小幅度大70%，说明β比1/k对温度更为敏感。这主要因为PA6熔体的黏度随着温度的升高而降低，所以1/k随温度的升高而减小;温度越高，PA6分子及其链段越容易自由运动，在多孔介质孔隙中受到拉伸作用产生的取向越容易发生解取向，此时所需转化为弹性能的能量就减少，从△P的角度则体现为弹性损耗下降，表现为β减小。

图4 1/k和β与温度的关系Fig.4 Relationship between 1/k or β and temperature

2.4 粘性损耗与惯性损耗分析

在整个熔体渗流过程中，粘性损耗和惯性损耗在△P中所占百分比例都随熔体流动速度的变化而变化。从图5可知，随着PA6熔体V的增加，不同过滤精度的多孔介质中由弹性引起的W都增加，增加幅度为10.7% ～22.9%;并且过滤精度越高，增加幅度越明显。这主要由于随着V的增加，PA6分子及链段在多孔介质中流动时受到拉伸引起的弹性效应所储存的能量来不及释放，导致W逐渐增加;并且随着多孔介质过滤精度的增加，流道空隙减小，熔体流动轨迹更加曲折，使熔体流动时产生更多的拉伸收敛，从而W增加更明显。然而，在整个流动过程中，由弹性作用而引起的W为0.75% ～30.6%。由此可知PA6熔体在多孔介质中流动时产生的△P主要来自粘性损耗。

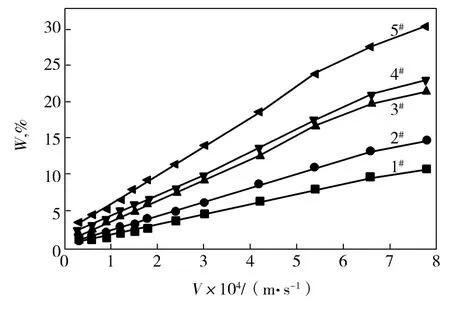
图5 W与V的关系Fig.5 Relationship between W and V

3 结论

a.PA6熔体通过多孔介质流动时，△P随着V与过滤砂精度的增大而增加。

b.PA6熔体通过多孔介质的流动状态函数中△P与V关系能够用Forchheimer方程较好地描述，在温度为265℃时，β比1/k大2个数量级;并且1/k与β都随着温度的升高而减小。

c.PA6熔体通过多孔介质时，△P主要来自粘性损耗，但随着V的增加，由弹性引起的惯性损耗增加，过滤精度越高，这种增加越明显。

［1］ Venkataraman P，Rao P R M.Validation of Forchheimer's law for flow through porous media with converging boundaries［J］.J Hydraul Eng，2000，126:63 －71.

［2］ Whitaker S.The Forchheimer equation:A theoretical development［J］.Trans Porous Media，1996，25(1):27 －61.

［3］ Nided D A，Bejan A.Convection in porous media［M］.New York:Springer Velag Inc，1999:124 －145.

［4］ 许元泽.高分子结构流变学［M］.成都:四川教育出版社，1990:187－206.

［5］ Bird R B，Dotson P J，Johnson N L.Polymer solution rheology based on a finitely extensible beads-spring chain model［J］.J Non-Newtonian Fluid Mech，1980，7(2/3):213 －235.