基于点估计法的微电网概率优化管理

陈家俊，蒋铁铮

(长沙理工大学 电气与信息工程学院，湖南 长沙410016)

0 引言

微电网作为智能电网的重要组成部分，近年来受到日益广泛的关注［1］。但是，各种不确定变量给微电网优化运行带来巨大影响。如何应对不确定性因素对微电网经济运行的影响值得深入的研究。目前，国内外学者已对微电网的经济运行问题进行了较多研究。文献［2］提出考虑小水电季节特性的微电网经济运行优化，建立了基于分时电价，以计及微网运行、网际交易、折旧等要素的总成本最低为优化目标，并运用APH 层次分析法，验证风-水互补运行对于提高微网经济性重要意义。文献［3］提出了动态微电网的概念。将多代理系统融入动态微电网的优化控制当中，并用改进的二进制粒子群算法求解该模型。文献［4］考虑风力随机出力的含风光柴蓄的独立微电网多目标优化，研究了不同风力以及日照条件下各机组输出功率的变化，从中选取典型调度方案，分析各组件功率，验证了模型的合理性。文献［5］考虑微电网中负荷不确定以及微电源出力随机性等，采用马尔科夫链模型和蒙特卡洛随机采样解决不确定问题，但是蒙特卡洛计算次数较多，计算时间较长。文献［6］全面考虑微电网中风力以及光伏发电、负荷的不确定性，分别建立相应的概率模型，采用半不变量法解决配电网概率潮流点估计法。文献［7］提出基于点估计法的含DG 配电网可靠性分析，将结果与卷积积分法相比较，指出点估计法出力不确定性的优越性。文献［8］提出点估计法在电压稳定性分析中的应用，考虑支路故障随机性的问题，建立相应的模型并且将结果与蒙特卡洛进行比较，验证了点估计具有较高计算精度以及较快的求解速度。文献［9］提出基于萤火虫优化算法的微网源-荷博弈模型及分析，利用算法的亮度和吸引度参数对相互博弈者的策略进行更新，通过算例验证该算法优越性。本文在充分借鉴点估计法在处理概率不确定性问题上的优势，依据风力和光伏输出功率和负荷的概率密度函数构造其出力和负荷需求的估计点，通过估计点与微电网经济运行之间关系，利用改进的萤火虫算法进行求解。

1 点估计法

点估计法是一类根据概率密度函数(PDF)中随机变量的概率分布求取待求随机函数各阶矩的概率统计方法，Hong 在Rosenblueth 的研究［10］的基础上提出了一种改进的点估计法［11］，其较高的计算精度和较低的计算成本使得其在工程系统不确定性问题研究中得到了众多关注。

假设分布式电源随机性以及负荷不确定相关影响因素用n 维随机变量x 函数Y表示:

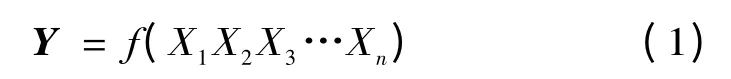
式中:X 为描述微电源出力以及负荷水平的随机变量所构成的随机向量;n 为随机变量的维数。

点估计法主要思想在于，通过DG 和负荷不确定性构成随机变量X1X2X3…Xn，由随机变量的概率密度函数f(xk)得到其高阶中心距Mj(Xk)，然后通过高阶中心矩构取出K 个估计点xk，ii=1，2，…，K，表征Xk概率分布特征。对每个点计算时保持X 的其他分量的值为期望值，这K，n 个点就组成了一个离散的分布，用这个离散的分布的各阶矩来估计总体Y 的各阶矩，得到Y 的统计信息。

根据每一个随机变量的均值μk和方差σk求取估计点:

式中:ξk，i为Xk取点xk，i时的定位系数。

位置系数和权重系数ωk，j之间的关系为

式中:λk，j称为标准中心距，为随机变量Xk的第j阶中心距Mj(Xk)和标准差σ 的j 方之比。

式中:f(xk)为随机变量xk的概率密度函数;Mj(Xk)为随机变量Xk的中心距。

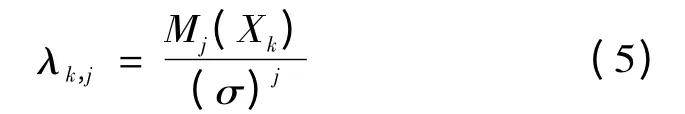
式中:σ 为变量Xk的标准差;λk，1=0，λk，2=1，λk，3，λk，4分别为随机变量Xk的偏度和峰度。对于两点估计法(k=2)，估计点的位置系数ξk，i和权重系数ωk，j如下:

随着随机变量个数n 的增加，估计点xk，1和xk，2将离其均值越来越远，可能会超出随机变量Xk的取值范围。

文献［12］指出当K=3 即三点估计法更加有效。此时位置系数和权重系数的计算为

当计及分布式电源出力以及负荷的不确定性时，在得到定位系数ξk，1和各估计点权重系数ωk，j后，根据力确定性函数关系可求得r 的各阶矩估计值

Y 的均值和标准差可表示为:

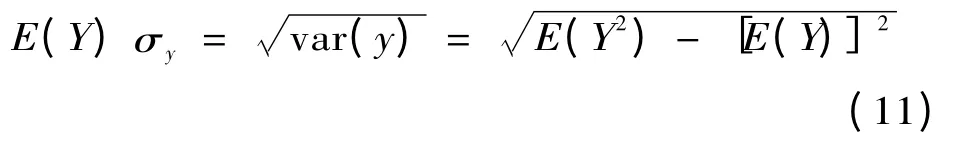
两点估计法与三点估计法相比计算简单，但是输入的随机变量Xk较多时，其估计效果不明显。而三点估计法，其中的一个点取平均值，因此三点法的计算次数仅比两点估计法多1 次，并且在构造估计点的同时，考虑了随机变量的峰度λk，4，其计算的效率与两点法非常接近，但是精度却明显高于两点法。

2 微电网的运行管理模型

2.1 风力发电的模型

多数研究指出风力发电机组的风速与输出功率之间的关系可以用威布尔风速表示［13］。风力发电输出功率的概率密度函数(PDF):

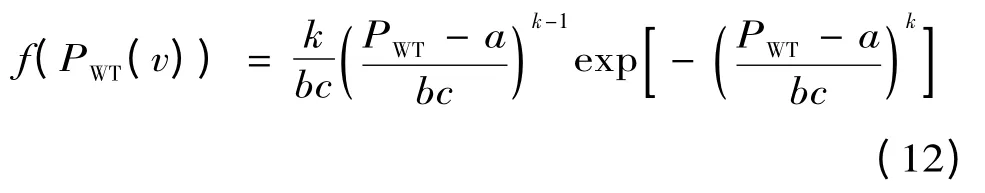
式中:k，c 为风速的威布尔分布的形状和尺度;a=Prvci/(vci- vr);b=Pr/(vr- vci);vci是切入风速;vr为额定风速;Pr为额定风速下风力发电机输出功率。

2.2 光伏发电模型

假设光照强度I 近似服从Beta 分布，则光伏发电输出功率的概率密度函数表示如下14］:

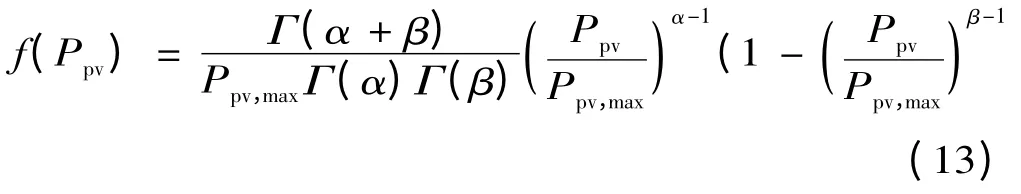
式中:Ppv，max是光伏发电最大输出功率;α，β 是Beta函数的形状参数。

2.3 负荷模型

负荷模型可以用正态分布模型描述，本文采用负荷模型表述如下［15］:

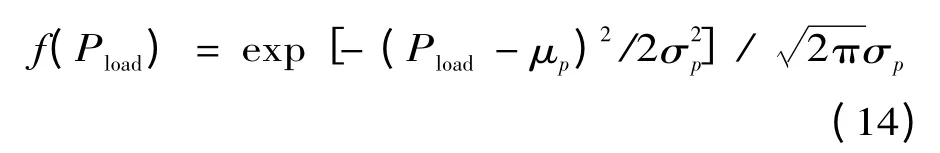
式中:μp/σp指的是负荷的平均值和标准差。

2.4 微型燃气轮机模型

微型燃气轮机使用的燃料包括天然气、成品油、柴油和沼气。其发电费用表述如下:

式中:Cng为燃料的价格;QLHV为燃料的低热值;为燃料机的输出功率;为t 时刻燃料机的发电效率。

2.5 燃料电池

燃料电池主要将化学能转化为电能，其发电成本表述如下:

2.6 电池组

蓄电池实际可用容量S 是电池温度的函数

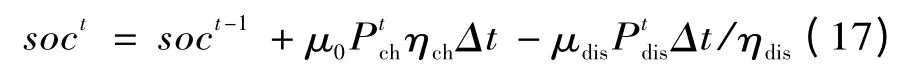
式中:soc 为电池充电状态;μch为1 时电池工作在充电模式，为0 时电池工作放电或者闲置模式。是有限时间内充电和放电的功率限制。μch/μdis为充放电的效率。

2.7 目标函数数学模型

微电网运行的总成本包括:发电成本以及运行维护的成本和系统购电成本。

式中:NG为发电单元的个数;Ki为个发电机组维护费用;分别为表示发电单元i 的输出功率、从微电网购买的电量、当前的用电费用。T为运行总的时间。

等式约束

不等式约束

(1)电源出力约束

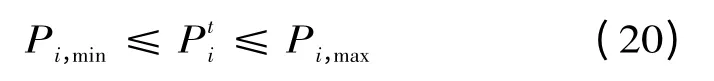
式中:Pi，min，Pi，max分别为代表输电电源最大和最小输出功率。

(2)机组爬坡速率约束

式中:ri，upΔt，ri，downΔt 为输电机组爬坡速度上下限。

(3)电池充电约束

式中:socmin，socmax为池容量上下限;Pch，max，Pdis，max是单位时间段内最大的充放电功率。

3 萤火虫算法

3.1 FA 优化机理

FA 算法是由杨新射等人通过模拟自然界萤火虫的群体行为而提出智能优化算法［16］。

将微电网经济运行目标函转化为萤火虫个体亮度，每一个萤火虫根据自己亮度(即目标函数优劣)决定空间位置更新，亮度较亮的具有较强的吸引能力。将萤火群体之间的互相吸引转化为目标函数求解过程。

3.2 FA 算法数学描述

从数学角度对萤火虫算法优化过程描述如:定义1:萤火虫的相对荧光亮度为

式中:I0为萤火虫的最大萤光亮度，即自身(r=0)荧光亮度;γ 为光强吸收因子，表示亮度受传播介质的影响而变化的特性，设为常数;rij表示萤火虫i 与萤火虫j 的空间距离。

定义2:萤火虫的吸引度为

式中:β0为最大吸引度，即最大荧光亮度所处位置的吸引度大小。

定义3:萤火虫i 在向比其亮的萤火虫j 移动时，空间位置的更新遵循下列公式

式中:x(i)表示萤火虫的初始化空间位置，在这里α［rand-0．5］是一个随机扰动，避免陷入局部最优值。

3.3 FA 算法改进

3.3.1 混沌搜索策略

为了避免陷入局部最优解，在算法种群初始化时候利用混沌搜索策略保持种群多样性。基本思想:将控制变量通过self-logical mapping 函数来产生混沌序列的取值区间内，采用混沌搜索的随机性和遍历性以及规律性寻优搜索，然后将优化解线性转化到解空间中［17］。混沌序列产生的数学表达式为:

式中:n=0，1，…，N;s=0，1，…，d;y(n)，s∈(-1，0)∪(0，1);d 是解空间的搜索维度;N 是混沌序列的最大迭代次数;bi，s，ai，s分别是xi，s最大值和最小值。

应用产生混沌序列的3 个步骤:

(1)将位于D 解空间中第i 个萤火虫个体，利用公式(27)映射到［-1，1］上。

(2)利用公式(26)产生新的混沌序列y(n+1)，s。

(3)最后根据公式(28)得到新的xi，s个体，带入目标函数求取适应度值。

在混沌序列产生中，寻找到更高质量的解，则将其代替原始萤火虫i 个体的原先位置;否则，继续进行混沌搜索，直到达到最大迭代次数。

3.3.2 引入全局最优值

从萤火虫的更新位置公式(25)可以发现，萤火虫的寻优只与周围的萤火虫的亮度有关，这里忽略了全局最优值［18］。本文在萤火虫的移动过程中引入全局最优的思想，在改进算法的每次迭代中处于当前全局最优的萤火虫可以影响周围的萤火虫，并吸引它们向自己移动。

在改进的萤火虫算法中，使用笛卡尔距离来计算其他萤火虫与当前处于全局最优萤火虫位置的距离，计算公式如下:

式中:Xgbest表示全局最优值的位置;rigbest表示当前萤火虫与全局最优值萤火虫之间的距离。

3.3.3 微电网概率优化管理求解步骤

(1)导入原始数据:确定目标函数内随机变量及其个数n 以及算法的相关参数，本文考虑风电的随机性以及光伏发电不确定性等、负荷不确定性。然后利用各自概率密度函数(PDF)求得各高阶中心矩，由式(6)求得λk，i。

(2)通过公式构造出估计点:由式(8)或(9)求出各估计点位置系数ξk，i以及权重系数ωi，j，然后通过式(2)求各变量的估计点xk，i。

(3)利用改进萤火虫算法对每个估计点xk，i进行优化式(18)给出模型，得到每一个估计点各个时间段的总运行费用。

(4)求出输出变量:由步骤(3)的结果代入式(4)得到各时间段总运行费用的各阶矩估计，然后利用公式(10)和(11)得到相应的均值和标准差信息。

4 算例分析

4.1 算例主要参数

本文图1 微电网系统为例［19］，系统包括风力发电、光伏发电、燃气机组、燃油机组、蓄电池机组。另外，此系统可以从电网购买电能。表1，2 分别是微电网系统的单元参数和不同时段的电价。图2，3，4 分别是24 h 风速以及日照强度和负荷变化。

图1 测试系统图

表1 DER 单元运行参数

表2 不同时段电价

图2 24 h 风速变化

微电网其他参数设置，Cng=1．98 REB/m3，ηFC=50%，ηMT=30%，QLHV=9．7 kW·h/m3，ηch=90%，soc0=200 kW·h，socmin=40 kW·h，socmax=360 kW·h。算法参数设置:萤火虫种群规模pop=30，最大迭代次数gen=200，步长因子α=0．25，初始吸引度β=0．2，光强吸引系数γ=1。

图3 24 h 日照强度

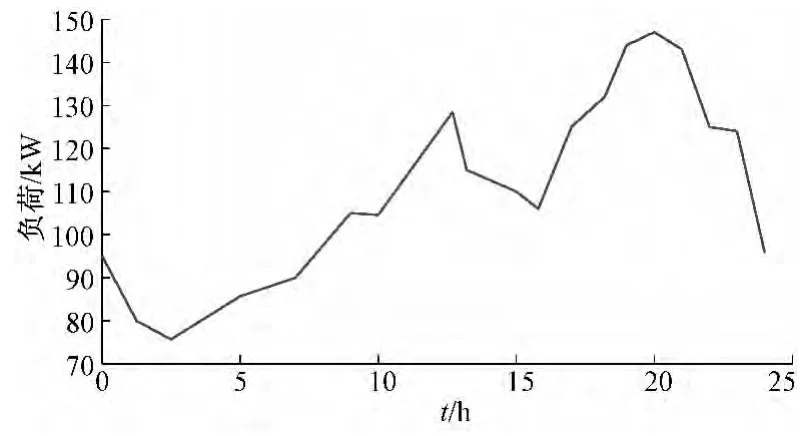
图4 24 h 负荷变化

4.2 算例结果分析

4.2.1 确定性分析

为验证本文改进算法具有更高优化能力，假设各个不确定性变量的变化与预测的相同。

图5 是进行独立20 次的最优情况下的收敛曲线，分析得出，MPSO 及FA 收敛速度较慢，并且容易陷入局部最小值。融入混沌策略丰富了萤火虫个体的行为，并能够调高种群利用率，使得算法能够避免陷入局部最优值，减少了无效迭代。另外，自适应调整策略，相对延长了算法探索和开发的过度过程，能够在寻优前期调高算法全局搜索能力，在后期提高算法的局部搜索能力。

表3 是3 种算法运行总费用的平均值以及标准偏差，从表3 中得出MFA 比较能够寻找更高质量的解，并且收敛速度也较快。

图5 算法收敛曲线图

表3 3 种算法寻优结果

图6 是使用本文算法得到的优化结果，分析得出，在负荷低谷时期，微电网购买大量的电能向负荷供电，并向电池充电。在负荷高峰时期，购电价钱较高时，电池开始放电，间接达到削峰填谷的作用。

图6 微电源1 天的输出功率

4.2.2 概率分析

本文中所有的随机变量都有确定概率密度函数，每一个时间的平均值都等于预测值，分布式电源的标准差取平均值的10%。为了研究负荷波动对于总运行成本的影响，分别取负荷标准差为平均值的2．5%，5%，10%。采用3 点估计法(3PEM)，即K=3 时，解方程组式(10)，求取各取值点的权重系数和位置系数。用Gram-Charlier 级数展开方法得到总费用的概率密度函数。

从表4 可以分析得出，运行总成本随着负荷不确定性的增加而增加，以弥补负荷波动。另外从表4 可以发现，三点法比二点法取值点要多，计算精度要高。

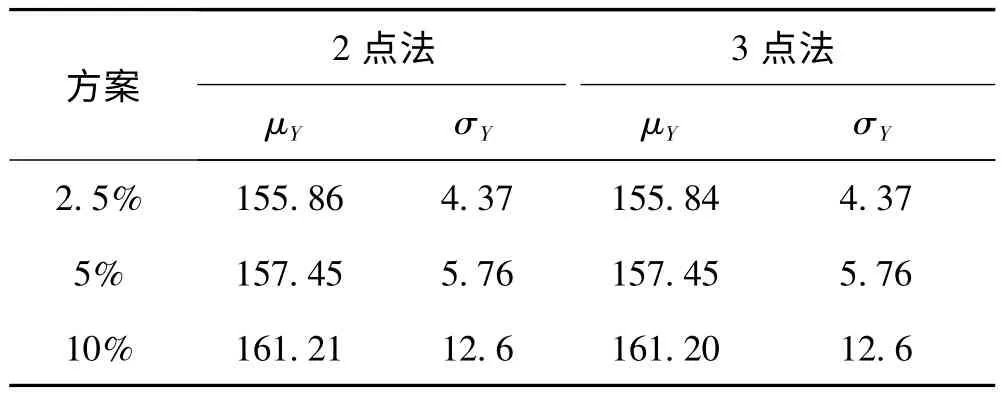
表4 3 种方法对比结果

在不同的负荷标准差取值下，应用三点估计法和本文改进萤火虫算法得到总运行费用的概率密度函数如图7 所示。

图7 概率密度函数

当负荷正态分布取方差为平均值的10%时，运行成本明显增加，三点法计算的结果总的运行成本以143 为均值，以5．6 为标准差。在150～160 千元之间呈高斯分布。当取值为5%时，运行成本以123 千元为均值，以6．5 为标准差，在150～165 千元之间呈高斯分布。当负荷正态分布取方差为平均值的2．5%时，运行成本以115 千元为均值，以6．2 为标准差，在145～178 千元之间呈高斯分布。

5 结论

(1)本文实现了点估计法在分析风光以及负荷不确定性的出力，通过各自概率密度函数，构造相应的取值点，评估不确定性对于微电优化管理影响，研究了负荷波动对于运行总成本的影响，并将结果与其他方法进对比，验证点估计法优点。

(2)提出改进的萤火虫算法，该算法引入混沌理论以及自适应调整策略的思想，对FA 算法进行混沌序列初始化，提高种群的利用率，然后利用自适应调整控制算法的参数，兼顾算法的开发和探索能力，最后通过算例验证所提算法具有较好适应性。

［1］Basu A K，Chowdhury S P，Chowdhury S，et al．Microgrids:energy management by strategic deployment of DERs-A comprehensive survey［J］．Renewable and Sustainable Energy Reviews，2011，15(9):4348-4856．

［2］黄伟，崔屹平，黄婷，等．考虑小水电特性季节特性的微网经济运行［J］．现代电力，2014，31(1):1-6．

［3］王兆宇，艾芊．基于QPSO 与BPSO 算法的动态微电网多目标优化自愈［J］．电网技术，2012，36(10):23-29．

［4］路欣怡，黄扬琪，刘念，等．含风光柴蓄的海岛独立微电网多目标优化调度方法［J］．现代电力，2014，31(5):43-48．

［5］茆美琴，周松林，苏建徽，等．基于风光联合概率分布的微电网概率潮流预测［J］．电工技术学报，2014，29(2):55-63．

［6］余昆，曹一家，陈星莺，等．含分布式电源的地区电网动态概率潮流计算［J］．中国电机工程学报，2011，31(1):20-25．

［7］芦晶晶，赵渊，赵勇帅，等．含分布式电源配电网可靠性评估的点估计法［J］．电网技术，2013，37(8):2250-2257．

［8］吴蓓，张焰，吴越，等．点估计法在电压稳定性分析中的应用［J］．中国电机工程学报，2008，28(25):38-43．

［9］王晶，王宗礼，陈俊宇，等．基于萤火虫优化算法的微网源—荷博弈模型及分析［J］．电力系统自动化，2014，38(21):7-12．

［10］王宇，贾志刚，李晓，等．边坡模糊随机可靠性分析的模糊点估计法［J］．岩土力学，2012，33(6):1795-1800．

［11］魏刚毅．基于点估计法的时变随机疲劳分析及其应用［D］．重庆:重庆大学，2014．

［12］杨欢，邹斌．含相关性随机变量的概率潮流三点估计法［J］．电力系统自动化，2012，36(15):51-56．

［13］余洋，陈盈今，刘立卿，等．大规模风电接入对电网电压稳定性影响的研究［J］．电力科学与工程，2010，26(4):1-4．

［14］刘芃伶，郭薇，马燕峰，等．家庭太阳能分布式并网发电系统［J］．电力科学与工程，2014，30(5):17-22，55．

［15］Lei D，Cheng W D，Bao H，et al．Probabilistic load flow analysis for power system containing wind farms［C］．Power and energy engineering conference(APPEEC)，Chengdu，China，28-31 March，2010:1-4．

［16］Yang X S．Nature-inspired Metaheuristic Algorithms［M］．Frome，U K:Luniver Press，2008:83-96．

［17］周勇，陈家俊，姜飞，等．基于改进萤火虫算法的分布式电源优化配置研究［J］．现代电力，2014，31(5):54-58．

［18］刘鹏，刘弘，郑向伟，等．基于改进萤火虫算法的动态自动聚集路径规划方法［J］．计算机应用研究，2011，28(11):4146-4149．

［19］Li P，Xu D．Optimal operation of microgrid based on improved binary particle swarm optimization algorithm with double-structure coding［C］．2014 International Conference on Power System Technology，2014:3141-3146．