输电线温度及载流量ANSYS 计算方法及修正因数

陈锡阳，刘 洋，马燕鹏，刘云鹏，吴振扬

(1．广东电网公司 东莞供电局，广东 东莞523000;2．华北电力大学 河北省输变电设备安全防御重点实验室，河北 保定071003;3．华北电力大学 数理学院，河北 保定071003)

0 引言

我国在架空输电线路设计中，载流量的计算模型主要采用摩尔根计算公式，采用的气象条件分别为风速0．5 m/s、日照强度1 000 W/m2、环境温度40 ℃等［1］。文献［2，3］利用ANSYS 仿真实际运行线路在一定载流下的导线温度，计算发热率时日照强度参数取固定值1 000 W/m2，但是实际运行时，日照强度随季节、地域不同而变化，其大小对输电线温度和载流能力具有重要影响。文献中仿真结果与摩尔根公式计算结果之间存在误差，虽然误差在工程误差允许范围内，但文献中并未对误差影响因素进行分析研究。

因此，本文采用ANSYS 仿真时，综合考虑日照强度随季节的变化情况，使其更加接近实际线路运行所处的气象环境。并采用摩尔根公式计算相同载流量下的导线温度，计算参数取仿真相对应的日照强度值，校验ANSYS 仿真结果的准确性，并进行误差分析。分析日照强度、复合散热系数及载流量大小对误差的影响，并根据分析结果，确定误差影响因素，并利用Matlab 进行多元线性回归分析法提出修正因数，使ANSYS 仿真结果更加精确。

1 ANSYS 热分析的基本原理及仿真结果

ANSYS 热分析的基本原理是将所处理的物理系统划分成有限个单元，根据能量守恒原理求解一定边界条件和初始条件下每一个节点处的热平衡方程，从“场”的角度通过数值方式求解导线的温度场，进而计算导线载流量［4］。

1.1 数学模型建立

以LGJ240/40 钢芯铝绞线为例，在ANSYS 中以导线中心为坐标原点，建立导线的3D 模型［5］，导线内外径分别为7．98 mm，21．66 mm，如图1。

钢芯铝绞线内部三维热传导方程、初始条件、第三类边界条件为

图1 钢芯铝绞线仿真模型

式中:t 为导线温度;λ 为材料热导率;x，y，z为空间直角坐标;φ1为钢芯单位体积的发热率;φ2为铝线单位体积的发热率;ρ 为材料密度;c 为材料比热容;τ 为时间;t0为初始温度;q 为外表面某一点的热流密度矢量;n 为该点的等温线上的法向单位矢量;acon为对流散热系数;tw为导线表面温度;tf为环境温度，此处取20;qr为导线表面与周围介质之间的净辐射换热热流密度;S 为导线的外表面。

1.2 发热率计算

钢芯、铝线单位体积的发热率φ1，φ2为

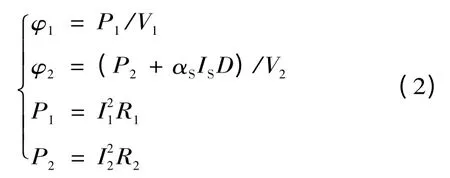
式中:P1，P2为单位长度的钢芯、铝线通电后的发热功率;V1，V2为钢芯和铝线的体积;I1，I2为钢芯和铝线中的载流量;R1，R2为单位长度的钢芯、铝线电阻值;αS为导线的吸热系数;D 为导线计算外径;IS为日照强度。

(1)文 献［2，3］中 IS取 我 国 标 准 值1 000 W/m2，本文考虑各种方位因素的影响［6～9］，采用CIGRE 中日照吸收热量的计算方法来计算。

导体单位长度吸收的太阳热量为:

其中

式中:HS为太阳高度角;γS和γC分别为太阳和导体的方位角;Φ 为季节变化引起的角度变化;η 为阳光的等效入射角;δS为赤纬角度;N 为1 年当中日照的天数;Z 为太阳的分时角度，从正午为0°开始，以每小时15°变化;ID为阳光直射热量;Id为阳光散热热量，晴朗天空取直射热量的10%;F 为反照率，此处取0．2;αS对于光亮的导体为0．27，工业环境下风化导体取为0．95，一般取为0．5。

选取北纬38°为代表地域，以此地理参数计算6 月及12 月份正午12 点的日照强度及太阳热量值，结果如表1。

表1 日照强度及太阳热量值

(2)文献［2，3］中R1，R2均取直流电阻值，文献［10］中用集肤效应系数和铁损系数的乘积表示交直流电阻比，但在工程计算中过于复杂。通常，钢芯铝绞线的交直流电阻比范围在1．016 4～1．022 4 之间，因此，本文选用固定值1．02［11］。则交流电阻计算公式为

导线参数取值如表2。

表2 导线参数取值

1.3 复合散热系数计算

表面散热由对流散热和辐射散热共同作用，该作用可用复合散热系数α 来统一描述。

表面的散热功率为

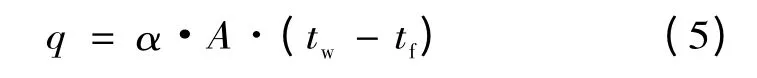
式中:A 为散热面积;tw为导线温度;tf为环境温度;α=α1+αrad，α1为强制对流系数，αrad为辐射散热系数。

本文只考虑强制对流情况，风速取为1 m/s，分别计算此风速下的强制对流系数α1与辐射散热系数αrad。由此得到钢芯铝绞线外表面在不同温度时的复合散热系数α，结果如表3。

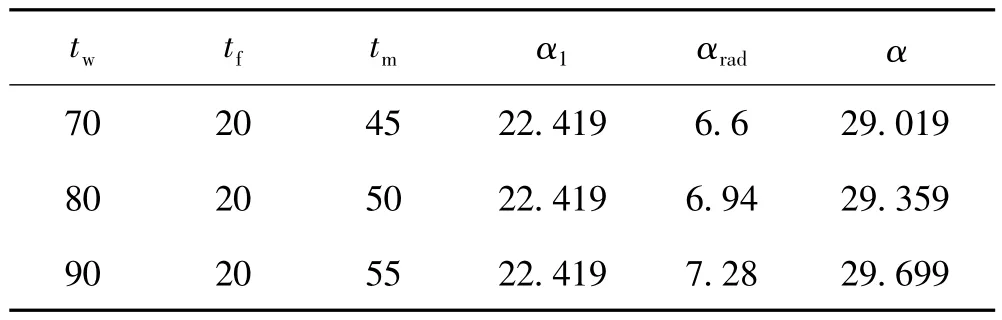
表3 复合散热系数计算结果(风速1 m/s)

1.4 仿真结果

利用ANSYS 仿真载流量由440 A 增加到800 A 时导线的温度，复合散热系数分别取29．019，29．359 和29．699，导线温度仿真结果如表4。

表4 载流量I 与导线温度t 的关系(风速1 m/s)

由表4 可知，钢芯铝绞线的温度随着导线载流值的增大而单调增加，随复合散热系数的增大而单调减小，且随着季节的变化，导线温度相差较大。

2 误差分析

2.1 摩尔根公式计算结果

根据仿真参数，采用摩尔根公式计算相同载流量作用下的导线温度［12～14］，结果如表5。

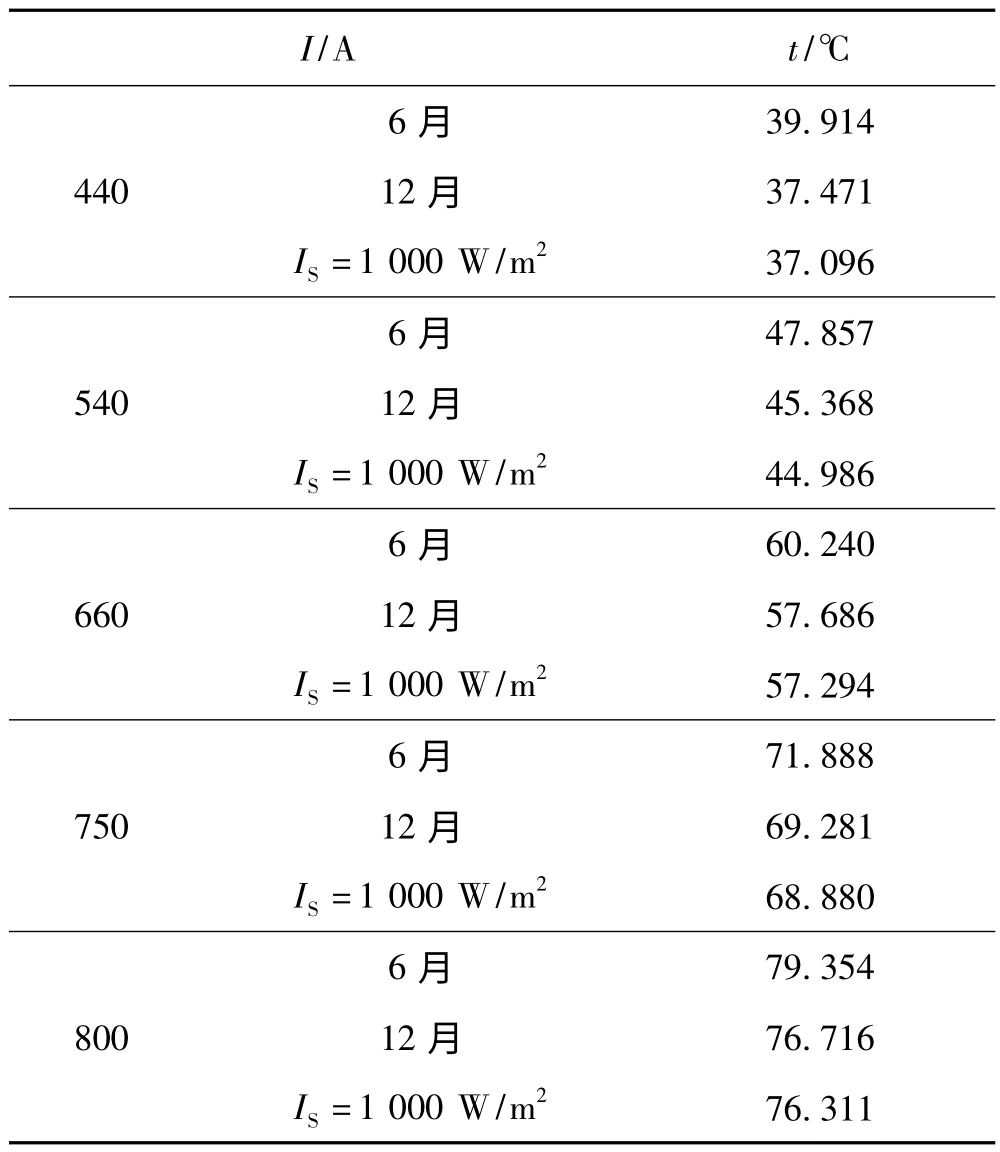
表5 摩尔根公式计算结果

2.2 误差影响因素分析

以摩尔根公式计算结果为准，对比分析不同日照强度、不同复合散热系数下的仿真结果与计算结果，得出仿真结果与计算结果的相对误差，即误差=×100%，并作出误差曲线图，如图2。

(1)由图2(a)可以看出，随日照强度的变化仿真误差基本不变，处于一个固定值，可知日照强度的变化对误差影响很小，可以不考虑日照强度的影响。

(2)由图2(b)可以看出，仿真误差随复合散热系数的增大而减小，基本呈线性关系，可知复合散热系数的变化对误差有一定影响。

(3)综合图2(a)、(b)两幅误差曲线图可以看出，仿真误差整体随仿真载流量的增大而减小，基本呈线性关系，可知载流量的变化对误差有一定影响。

由此可知:修正因数为复合散热系数与载流量的数学关系式，并可以根据两者与误差的线性关系提出修正因数的基本关系式。

图2 误差曲线

3 修正因数及修正结果

3.1 修正因数

忽略日照强度对误差的影响，选取IS=1 000 W/m2时的仿真结果进行修正。针对载流量及复合散热系数两种影响因素，利用Matlab 多元线性回归分析方法，分析的数据如表6。

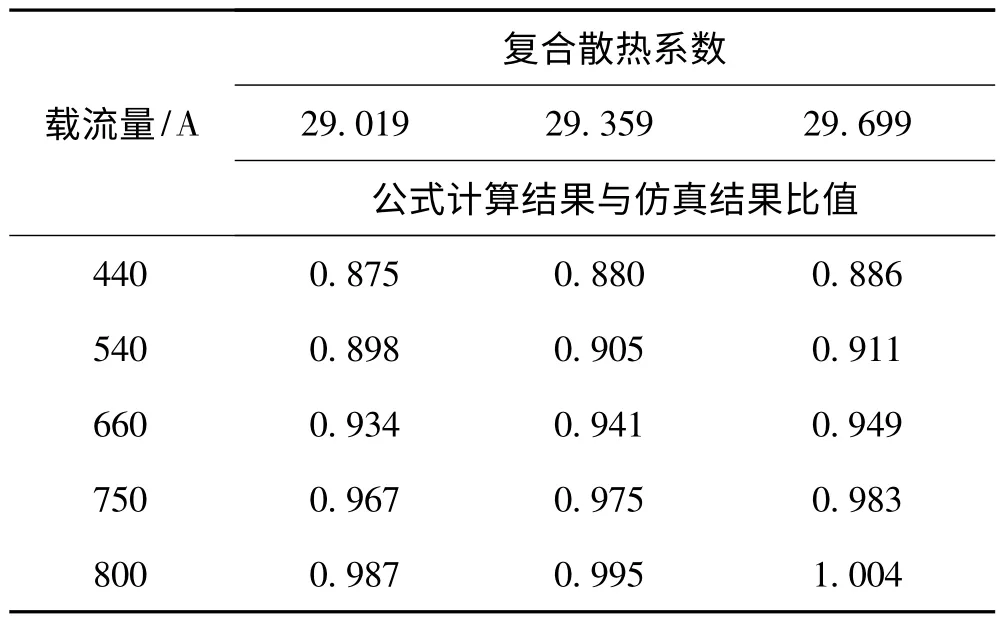
表6 分析的数据

取公式计算结果与仿真结果比值为y，即修正因数。以复合散热系数与载流量为两个变量x1，x2，Matlab 多元线性回归分析结果为

由结果可知:r2=0．991 8≈1，表明回归模型与数据十分吻合;显著性水平p=0 ＜0．05，表明回归模型与数据存在显著性相关。因此确定回归模型成立，修正因数y 关系式成立。

3.2 修正结果

将修正因数y 代入仿真结果中，可得到修正结果，修正前后误差曲线对比图如图3。

图3 修正前后误差曲线对比图

图3 中，第一象限中3 条曲线为修正前的不同复合散热系数下的误差曲线，第四象限为修正后的不同复合散热系数下的误差曲线，可以看出修正后误差均处在-2．23%～-0．82%之间，且载流量与复合散热系数对误差的影响很小。由此可见修正因数的选取是合理的、准确的。

4 结论

ANSYS 仿真结果与摩尔根公式计算结果存在一定误差，以摩尔根公式计算结果为准，分析仿真误差影响因素，结果表明:日照强度的变化对误差影响很小，可以忽略日照强度对误差的影响;误差随复合散热系数的增大而减小，随仿真载流量的增大而减小。由此针对载流量及复合散热系数两种影响因素，提出了修正因数，利用Matlab多元线性回归分析法，得出了修正因数的数学关系式，并对仿真结果进行修正。修正结果表明:代入修正因数后，ANSYS 仿真结果更加准确，由此计算输电线温度及载流量更加准确、可信。

［1］DL/T 5092-1999．110～500kV 架空送电线路设计技术规程［S］．

［2］何整杰，李震彪，梁盼望．输电线温度及载流量的ANSYS 计算方法［J］．浙江电力，2010，29(8):1-5．

［3］何整杰．220kV 输电线路增容研究［D］．武汉:华中科技大学，2009．

［4］韩芳，徐青松，候炜，等．架空导线动态载流量计算方法的应用［J］．电力建设，2008，(1):39-43．

［5］张建伟，白海波，李昕．ANSYS 14．0 超级学习手册［M］．北京:人民邮电出版社，2013．

［6］IEEE Standard 738-2006 IEEE Standard for Calculating the Current-Temperature of Bare Overhead Conductors［S］．

［7］Schmidt N P．Comparison between IEEE and CIGRE ampacity standards［J］．CIGRE Transactions on Power Delivery，1999，14(4):1555-1559．

［8］张辉，韩学山，王艳玲．架空输电线路运行载流量分析［J］．电网技术，2008，32(14):31-35．

［9］张辉．运行条件下输电线路热载荷能力研究［D］．济南:山东大学，2008．

［10］林玉章．高压架空输电线路载流量和温度计算［J］．南方电网技术，2012，6(4):23-27．

［11］丁咏竹．基于参数辨识的输电线路热容量评估［D］．重庆:重庆大学，2012．

［12］叶鸿声，龚大卫，黄伟中，等．提高导线允许温度的可行性研究和工程实施［J］．电力建设，2004，25(9):1-7．

［13］Chen S L，Black W Z，Loard H W．High Temperature Ampacity Model for Overhead Conductors［J］．IEEE Transactions on Power Delivery，2002，17(4):1136-1141．

［14］陈锡阳，王艳玲，黄河，等．一种新的架空输电线路安全限距计算模型［J］．电力科学与工程，2015，31(2):60-65．