一种新型升降压DC-DC变换器的建模与控制

吴苓芝， 丁新平， 魏文健， 王伯荣， 王天兵

(青岛理工大学 自动化工程学院，山东 青岛 266520)

一种新型升降压DC-DC变换器的建模与控制

吴苓芝， 丁新平， 魏文健， 王伯荣， 王天兵

(青岛理工大学 自动化工程学院，山东 青岛 266520)

对一种新型升降压DC-DC变换器进行了研究，新型变换器具有任意升降压功能，对稳态时的工作原理进行了分析，根据状态空间平均法建立了新型升降压DC-DC网络在电流连续工作模式下(CCM)的交流小信号模型，对模型进行分析，获得了控制至输出的传递函数，实现了输出电压闭环控制。最后建立实验样机，进行了实验验证，实验结果与理论分析相吻合。

升降压；DC-DC变换器；状态空间平均法；小信号模型；闭环控制

0 引 言

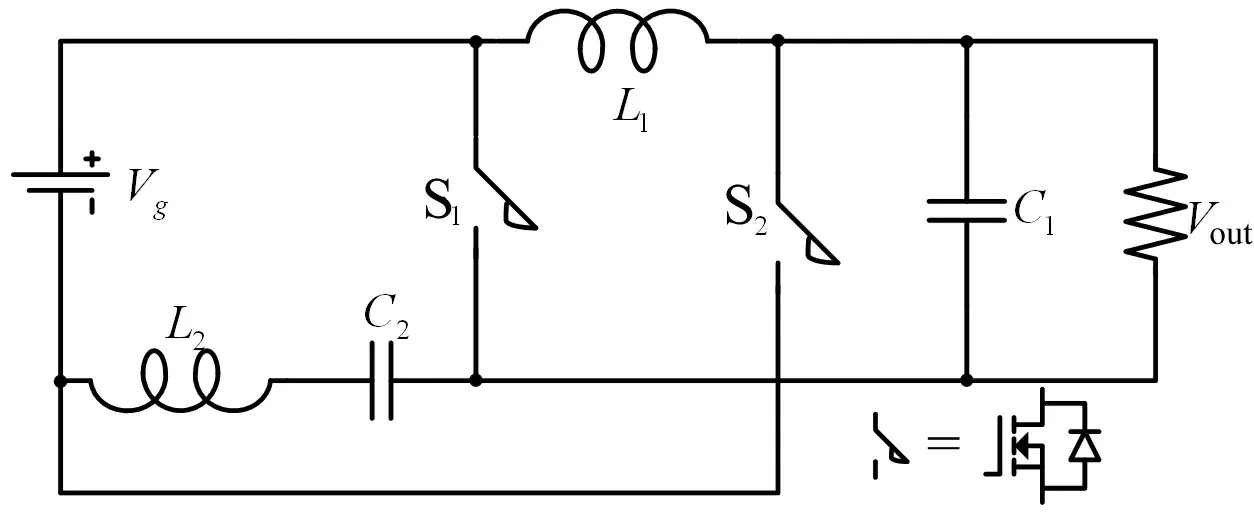
图1 新型升降压DC-DC网络

具有任意升降压功能的新型升降压DC-DC变换器如图1所示。对电力电子电路进行分析与控制，其前提是对它的网络拓扑进行建模。根据状态空间平均法建立了新型升降压DC-DC网络在电流连续工作模式(CCM)下的交流小信号模型[1]，获得了控制至输出的传递函数，为新型升降压DC-DC网络设计控制策略提供理论依据。

1 稳态分析

稳态时，新型升降压DC-DC变换器运行在CCM模式下的两种工作状态，其工作原理等效电路如图2所示。设一个开关周期内，开关管S1的导通时间为T0，关断时间为T1，则有：T0+T1=TS。

图2 稳态时新型升降压DC-DC网络的两个等效电路

开关管S1导通时的状态等效电路如图2(a)所示，回路Vg-L2-C2和回路L1-C1(Rload)同时导通，该状态持续的时间为T0。电感L1和L2两端的电压分别为：vL1=-VC1<0，vL2=-Vg-VC2<0，电感电流在负电压的作用下线性下降，在本时段末达到最小值。

开关管S1关断时的状态等效电路如图2(b)所示，回路Vg-L1和回路Vg-L1-C1-C2-L2同时导通，该状态持续的时间为T1。电感L1和L2两端的电压分别为vL1=Vg，vL2=VC1-VC2，电感电流在正电压的作用下线性增加，在本时段末达到最大值。

在稳态条件下，一个开关周期内电感L1和L2两端的平均电压必须相等[2]，否则从一个周期到下一周期，电感电流会产生一个净增加量或减少量，就不是稳态了。所以:

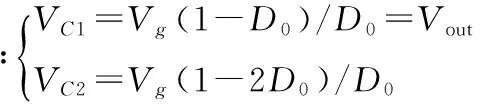
其中D0为开关管S1导通时的占空比。

2 动态模型

2.1 平均状态空间模型

在推导过程中考虑电感寄生电阻r1、r2和电容等效串联电阻R1、R2的影响[3]。选电感电流iL1、iL2和电容电压vC1、vC2为系统状态变量，选输入电压vg、负载电流io及直通占空比d0为模型的输入信号。在CCM模式下,新型升降压DC-DC网络的整个工作过程分为直通模式和非直通模式[4]。

开关管S1导通时的状态等效电路如图3(a)所示，开关管S1关断时的状态等效电路如图3(b)所示，两种状态下，新型升降压DC-DC网络的状态方程分别为:

式中

其中p=d/dt-微分算子；L、C-电感值和电容值；r=r1=r2-电感寄生电阻；R=R1=R2-电容等效串联电阻；io-负载电流；vg-输入电压。

采用状态空间平均法对新型升降压DC-DC网络进行建模，新型升降压DC-DC网络的状态平均方程如下：

(1)

其中A=d0A1+d1A2；B=d0B1+d1B2；d0-动态占空比；<·>TS-开关周期内的平均值。

稳态工作时，新型升降压DC-DC网络电感伏秒平衡，电容安秒平衡，由此得网络的静态工作点为：

AX+BU=0

(2)

其中A=D0A1+D1A2；B=D0B1+D1B2；D0-静态工作点的占空比；D1=1-D0；

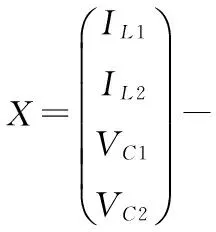
求解方程(2)，得到系统稳态工作时的电感电流和电容电压分别为：

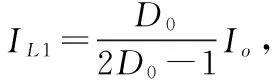
忽略电感寄生电阻r和电容等效串联电阻R，结果和前述稳态工作时的值是一致的，证明了平均状态空间模型的正确性。

2.2 小信号模型

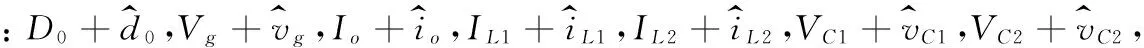
(sE-A)x(s)=Bu(s)+[(A1-A2)X+
(B1-B2)U]d0(s)

(3)

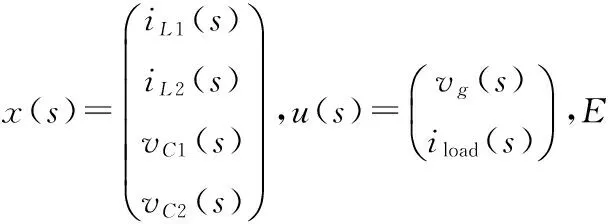
x(s)=(sE-A)-1{Bu(s)+
[(A1-A2)X+(B1-B2)U]d0(s)}

(4)

令k=L2Cs3+2(r+R)LCs2+(2D02r-2D0r+D0R+r)+[(r2+2R2D0-R2D02+2rR)C+(2D02-2D0+1)L]s，I11=IL1+IL2，V11=-RIL1-VC1-Vg-RIo，V12=-RIL2-VC1-Vg-RIo，求解方程(4)，得到两个电感电流和两个电容电压分别为：

(5)

(6)

(7)

其中：

在式(5)～(8)中，令其中两个输入为零，便可得到其中一个输入至系统状态变量的小信号传递函数。在式(7)中令vg(s)=0，io(s)=0，得到直通占空比至新型升降压DC-DC网络输出电容电压的传递函数为：

同理，可以得到任意某个输入至系统状态变量的小信号传递函数。

3 动态性能分析

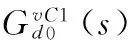
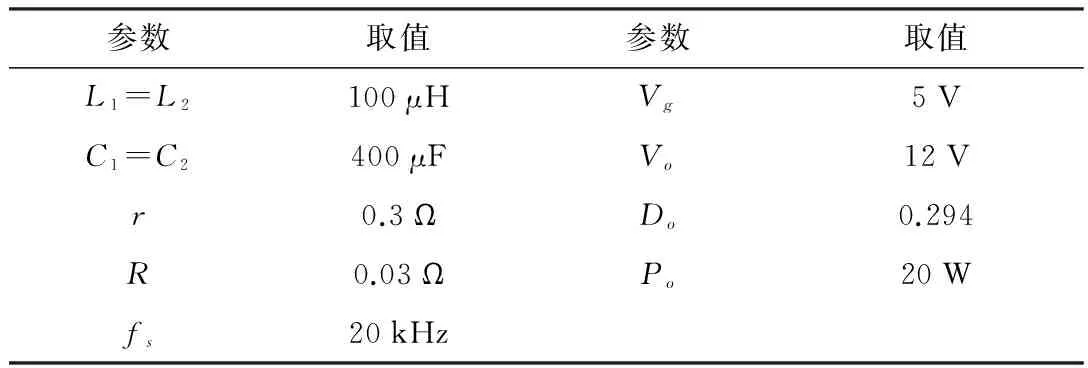
表1 系统额定工作参数

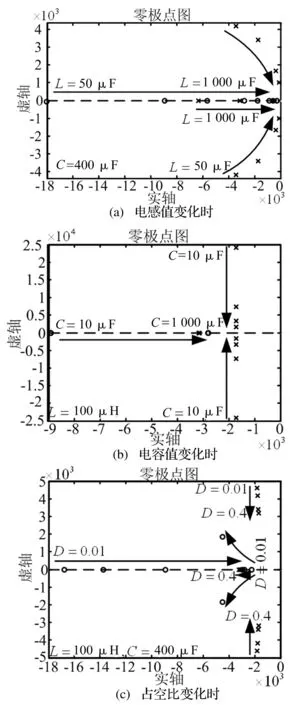
图3 参数变化时传递函数零极点分布图

从稳态工作状态考虑，电感值和电容值的取值越大，可以有效降低纹波电压和电流，但系统动态响应变慢使得非最小相位现象加剧，因此，系统设计时要综合稳态性能和动态响应速度合理的选择电容值和电感值。

为了设计出性能优良的系统，应该综合考虑电流纹波、电压纹波以及输出电压的动态响应来设计系统的无源元件，在此基础上设计系统控制的软、硬件，从而得到良好的系统。通过建立新型升降压DC-DC网络直通占空比-至-输出电容电压的小信号模型，能够定量的求出无源元件对变流器输出电压动态响应的影响。在系统参数一定时，可以据此给系统控制提供定量的参考依据。

4 输出电压闭环控制

由前面推导的小信号模型可知，系统的L、C参数一定时， 影响输出电压的因素有直通占空比、输入电压和负载电流。从控制的角度来看，输入电压扰动和负载电流扰动均可视为外部扰动，当电路有扰动存在时，通过调节直通占空比D0使输出电压保持恒定。采用反馈控制能够同时抑制电源电压和负载电流对输出电压的扰动，使输出电压保持稳定。系统输出电压闭环控制框图如图4所示。

图4 输出电压闭环控制框图

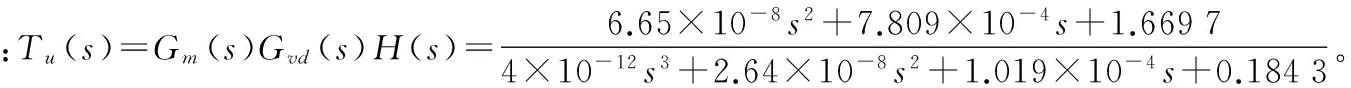
图5 补偿器前后的开环传递函数波特图

为了改善闭环系统的动态性能，同时增加低频段的开环增益，采用电容电压闭环控制，设计了式GC(s)=KP+Ki/s所示PI控制器[6]。取Kp=0.25，Ki=500，得到图5所示的电容电压控制补偿前后系

统的开环传递函数Bode图。电容电压补偿后系统的穿越频率约为1.2 kHz，相角裕度约为59度,系统的低频增益和动态性能得到了明显的提高。

5 实验验证

为了进一步验证理论分析的正确性，在实验室构建了30 W小功率数字电源进行性能分析，对元器件进行了参数计算[7]与选择，设计了新型升降压DC-DC变换电路实验样机。

图6为新型升降压DC-DC变换电路实现升压功能时的实验波形。输入接5伏，占空比D≈0.3时，稳态输出12伏，如图6(a)所示，符合理论计算和分析。图6(b)为输入从0突然变化为5伏时，输入输出电压的动态跟踪能力试验波形，在阶跃输入下，输入输出电压动态响应和静态误差都比较理想，完全满足电源系统需要。图6(c)为负载从23欧姆突变到72欧姆时，输入和输出电压的变化波形，系统对负载扰动具有一定的抑制能力，扰动发生后动态响应很快就进入扰动前的稳态输出电压，和理论分析结果非常吻合。

图7为新型升降压DC-DC变换电路实现降压功能时的实验波形。输入接15伏，输出电压为12伏时，占空比D≈0.6，如图7(a)所示，符合理论计算和分析。图7(b)是输入电压上电时系统的动态响应能力和抑制干扰能力试验波形，图7(c)是负载由23欧姆变为72欧姆时系统的动态响应能力和抑制干扰能力试验波形，扰动发生后，输入输出电压在很短的时间内即恢复到扰动前的稳定状态，试验结果和理论分析结果非常吻合。

图6 电路实现降压功能时的输入输出电压动态响应波形

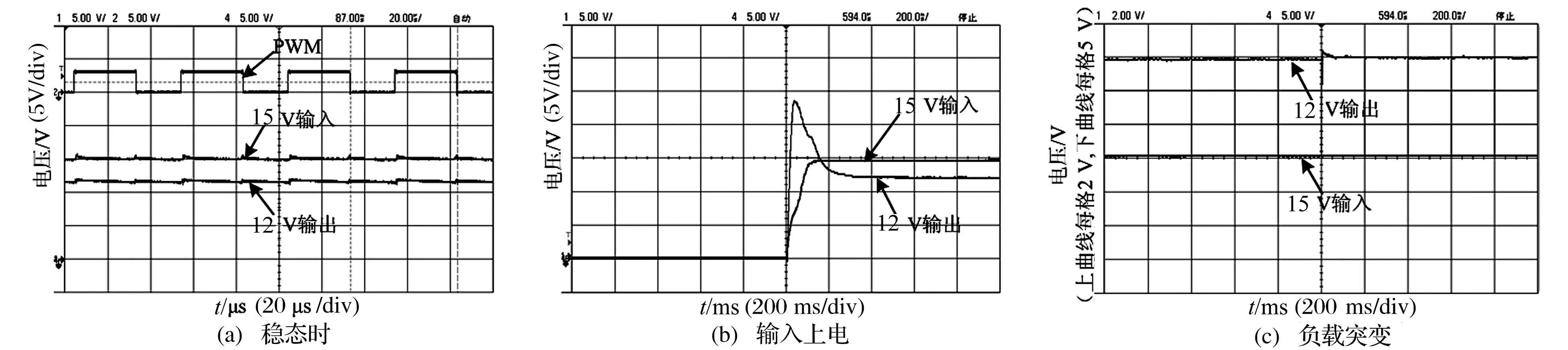
图7 电路实现升压功能时的输入输出电压动态响应波形

6 结束语

对新型DC-DC变换电路进行了稳态分析，根据状态空间平均法建立了系统小信号模型，实现了输出电压闭环控制，并进行了实验验证。实验表明，实验结果与理论分析相吻合。

[1] 徐德鸿. 电力电子系统建模及控制[M]. 北京：机械工业出版社,2005.

[2] JULIO CESAR ROSAS-CARO, FANG ZHENG PENG, HONNYONG CHA, et al. Z-source-converter-based energy-recycling zero-voltage electronic Loads[J]. IEEE Trans. on Industrial Electronics, 2009,56(12):4894-4902.

[3] YUAN LI,SHUAI JIANG, JORGE G,et al. Modeling and control of quasi-z-source inverter for distributed generation applications[J]. IEEE Trans. on Industrial Electronics, 2013,60(4):1532-1541.

[4] HAITHAM ABU-RUB,ATIF IQBAL,SK MOIN AHMED,et al. Quasi-z-source inverter-based photovoltaic generation system with maximum power tracking control using ANFIS[J].IEEE Trans. on Sustaimable Energy, 2013,4(1):11-20.

[5] ERICKSON, ROBERT W. Fundamentals of power electronics[M]. USA: Kluwer Academic Publishers, 2000.

[6] 胡寿松．自动控制原理[M]．5版.北京：科学出版社, 2007.

[7] SANJAYA MANIKTALA. Switching Power Supplies A to Z[M]. Newnes, 2006.

Modeling and Control of a Novel BUCK-boost DC-DC Converter

WU Ling-zhi, DING Xin-ping, WEI Wen-jian, WANG Bo-rong, WANG Tian-bing

(Qingdao University of Science and Technology, Qingdao Shandong 266520, China)

This paper discusses a novel buck-boost DC-DC converter capable of arbitrary bucking and boosting and analyzes its principle of operation in the steady state. In the state space averaging method, a small AC signal model is established for the novel buck-boost DC-DC network in the mode of continuous current mode (CCD). The model is analyzed to obtain the control-to-output transfer function and realize closed-loop control over the output voltage. Finally，an experimental prototype is set up and experimental verification is performed. The experimental results coincide with theoretical analysis.

BUCK-boost; DC-DC inverter; state space averaging; small-signal model; closed-loop control

山东省自然科学基金(ZR2013EEM020)

10.3969/j·issn.1000-3886.2015.02.002

TM46

A

1000-3886(2015)02-0004-04

吴苓芝(1986- )，女，山东人，硕士生，专业控制科学与工程。 丁新平(1975- )，男，甘肃人，副教授，博士，主要从事电力电子系统及应用研究。

定稿日期: 2014-07-18