特殊情况下标准偏差计算在船舶工程中的应用

徐 晖，李翠芳

（中船黄埔文冲船舶有限公司，广州510715）

1 简介

标准偏差在概率统计中最常使用于统计分布程度上的测量，它是总体各单位数值与总体算术平均数之间差值平方的算术平均数的平方根。

假设有一组实数值X1、X2、X3……Xn，其算术平均数为，则用于计算基于给定样本的总体标准偏差的公式为：

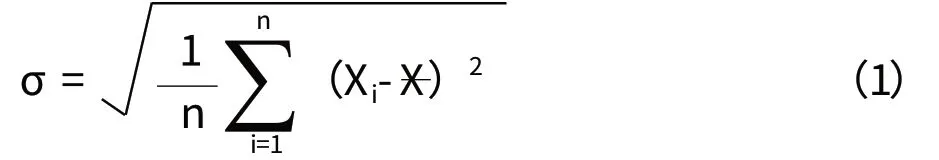
当用于估算基于给定样本的标准偏差时，其公式为：

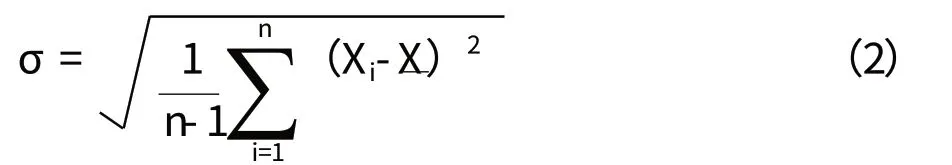
标准偏差用于表示组内各单位数值之间的离散程度，通常用作不确定性的测量，评估一组数据的离散程度。在船舶工程中，标准偏差常用来统计受检产品质量情况或评估受检设备的精确度。

2 工程应用

工程应用中，在误差平均值相同的情况下，样本的标准偏差越小，说明受检对象的测量数值离散度越小，精确度越高。

比如，某船厂购买的两个不同批次的直径要求为8 mm的电缆，经抽样检验A批次的电缆直径检测值ΦA为{8.1 mm、8.0 mm、7.9 mm、8.1 mm、8.0 mm}，B批次的电缆直径检测值ΦB为{8.2 mm、7.9 mm、7.7 mm、8.2 mm、8.1 mm}。两个批次的电缆直径与技术要求之间误差分别为：A批次{0.1 mm、0 mm、-0.1 mm、0.1 mm、0 mm}；B批次{0.2 mm、-0.1 mm、-0.3 mm、0.2 mm、0.1 mm}。

两个批次的电缆直径与技术要求之间误差的算术平均值为：

从两个批次的电缆直径与技术要求之间误差的算术平均值来看，两个批次的电缆直径质量是一样的。但如果分别计算A、B批次电缆直径误差的标准偏差，则有明显的区别：

从标准偏差的计算结果来看，A批次电缆的电缆直径离散度更小，电缆直径控制精确度更高，显然电缆的可靠性也提高。

3 工程应用中的特殊情况

在实际的船舶工程应用中，并不是所有的受检对象都有已知的真实值。这时可以利用已经过有效检定的较高精度的测量设备提供基准值，用于对受检设备的测量数据进行比较并进行测量误差、标准偏差计算。

例如，对船舶上安装的船舶定位仪器进行定位精度检查。由于船舶所处位置的不确定性，无法事先指定经纬度，此时可以利用精度较高的DGPS设备提供船舶所在位置经纬度，利用DGPS设备的测量数据作为基准值，对受检的船舶定位仪器进行检测，并计算出受检设备定位误差、定位精度。

然而，在个别特殊情况下，受检设备的测量值中包含有这样的叠加值：总体方向一致，数值大体一致，无法准确测量却又不可消除。在这样一种特殊情况下，沿用经常使用的标准偏差计算公式会使计算结果出现很大的偏差，导致误判甚至错判结果的出现。

比如，我公司目前建造的船舶上安装的计程仪设备，主要是压差式、电磁式和多普勒式三种，其中以压差式和电磁式最为普遍。从计程仪的工作原理可知，压差式和电磁式计程仪所测得的船舶航行速度值其实是船舶相对于洋流的速度。

假设船舶在以航向H及H±180°航行时，船舶航速保持恒定，使DGPS测得的基准航速保持为V；航向分别为顺流或逆流，洋流速度一直为VL，洋流方向保持不变。下面计算理想情况下的计程仪测量标准偏差。

计程仪设备测量的船舶航行速度分别为：

逆流VH1=V-VL

顺流VH2=V+VL

假设根据试验程序，船舶分别以航向H、H±180°、H航行了三趟测试线长，则得到：

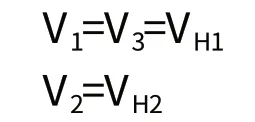
在进行测量结果计算时，V2进行两次计算，即可视为V4=V2，则有：

从以上计算结果可以发现，无论计程仪设备测量结果如何精确，计程仪设备的测量结果都存在着不可忽视的大离散度，并且该离散度大小与试验海区洋流速度大小成正比例的关系。这一计算结果根本无法准确反映计程仪设备的测量精确度,对计程仪设备的测量精确度判定有着严重的影响。

4 对原公式的处理

为了尽可能的消除洋流速度的影响，必须对原有的标准偏差计算公式进行调整。事实上，只要对原计算公式进行一个很小的处理，便可以在理论上消除洋流带来的负面影响。

计算每个航行线长上计程仪测量速度与基准速度之间误差时，对差值取绝对值，则有：

如计算结果所示，通过在误差计算时的取绝对值运算，可以有效的剔除洋流速度对标准偏差的计算影响，使计算结果能够准确的反映计程仪设备测量的精确度。

5 结束语

为了保证船舶的建造质量，不仅要严抓施工质量，从设计上也要考虑受检设备的检验、数据处理方法，才能更好更准确地检测设备的工作精确度，更有力保障产品的建造质量。