无记忆功放的预失真数学模型
侯道琪,杨 正
(电子工程学院,合肥 230037)
无记忆功放的预失真数学模型
侯道琪,杨 正
(电子工程学院,合肥 230037)
研究了无记忆功放的非线性特性,建立了正交基拟合模型,运用内积法求解了模型系数,进行了拟合研究和仿真。针对预失真处理,分别建立了伪记忆模型和伪记忆深化模型,运用了序贯最小二乘法,方便、高效地实现多模型中多个未知参数的求解,实现了功放的输入/输出线性化,进行了拟合仿真。
无记忆功放;预失真;模型;伪记忆
0 引 言
信号功率放大是电子通信系统的关键功能之一,其实现模块称为功率放大器(PA),简称功放[1]。功放输出信号相对于输入信号可能产生非线性变形,此现象称为非线性失真。功率放大器是无线通信系统的重要组成部分,随着数字信号处理能力的不断提升,数字预失真技术将会是以后的重点发展方向。预失真的基本思想是在放大器前构造放大器的逆特性,使预失真器和放大器的联合特性呈线性。
1 问题分析
对于攻放而言,如果某一时刻的输出仅与此时刻的输入相关,则称此攻放为无记忆功放。
本文主要是对无记忆功放的非线性特性进行研究并建立预失真模型,从而使得功放能够达到线性化要求的同时,满足“输出幅度限制”和“功率最大化”等各条件的约束。首先针对功放的非线性特性进行研究,建立非线性特性拟合模型,进而建立预失真模型,使得功放满足多目标优化,最后能够对所建模型进行归一化均方误差(NMSE)评价。
2 无记忆功放的非线性特性数学模型的建立与求解
本文主要是为了通过预失真数学模型改进功放的非线性特性,首先就需要对功放的非线性变形的具体形式进行深入的研究。通过将输入信号和输出信号的幅度和相位进行分离,得出结论:功放的输入/输出呈现非线性的变化,然而相位的变化呈现良好的线性特性。因此,在下面的分析研究中,着重对功放的幅度非线性特性进行研究。
2.1 无记忆功放的非线性特性分析和建立模型
2.1.1 正交基拟合模型的分析
根据函数逼近的Weierstrass定理可知,对解析函数G(x)总可以用一个次数充分大的多项式逼近到任意程度,故可采用计算简单的多项式表示非线性函数[2]。
多项式拟合阶数原则(PFOP):模型多项式的阶次取得太低,拟合就粗糙;阶次太高,拟合“过头”,使数据噪声也被纳入模型。因此,在多项式拟合中,阶数的确定要遵循以下2个基本条件:
(1)χ2量与自由度相近;
(2) 如果Q(χ2,N-(n+1))=1-P(χ2<(N-n-1))与0.5接近,则认为阶次适当。
经过对功放非线性特性的拟合多项式进行χ2量与自由度差值的仿真计算,得到图1中χ2量与自由度差图,可以看出在多项式拟合阶数接近6时,基本满足PFOP中的条件(1);进而对条件(2)进行验证,得到图1中拟合良好度图、拟合残差图和拟合偏差图,可以看出在多项式拟合阶数为5时是最理想的。
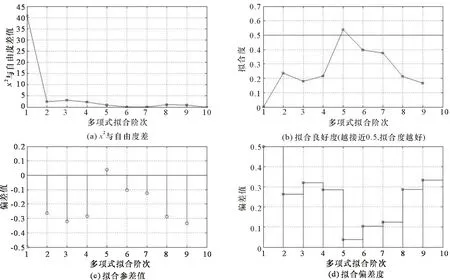
图1 多项式拟合阶次确定
2.1.2 正交基拟合模型的建立

(1)
式中:k=0,1,…。


表1 输出函数的正交基
从而得到正交基的多项式表达式为:
(2)
2.2 无记忆功放的非线性特性模型的求解
对正交基拟合模型的求解可以通过内积的计算方式:
(3)
得到z(t)中各项φi(x)的参数hi,如表2所示。

表2 正交基拟合模型输出函数的系数值
因此,得到的正交基拟合模型为:
z(t)=0.27φ5(x)+(-0.75)φ4(x)+ 0.85φ3(x)+(-1.64)φ2(x)+ 3.72φ1(x)+(-0.54)φ0(x)
(4)
依据正交基拟合模型得到的对比曲线如图2所示。

图2 正交基模型拟合对比曲线
在所建立的正交基拟合模型的基础上,运用NMSE对所得到的正交基拟合模型进行模型准确度评价,得到正交基拟合模型的评估值为-62.75dB。
3 无记忆功放预失真数学模型的建立与求解
在无记忆条件下研究预失真模型,最关键的就是使得功放非线性的特性在加入预失真模块后能够实现线性化。其次还应充分考虑功放最大输出幅度不能超过功放的可承受范围[3]。
在建立预失真模型得到理论的功放线性化输出的基础上,通过真实输入输出数据的实验,得到模型的结果数据。进而将输出结果与理论模型进行误差分析,得到预失真补偿后的归一化均方误差。
本文分析研究了无记忆功放与有记忆功放的输入/输出数据。可以看出,在存在记忆的情况下,功放输入/输出信号的幅度和相位都表现出较好的线性特性。通过分析可以说明,如果“人为”将无记忆性的功放作为有记忆功放进行处理,也就是在预失真处理中,使得当前瞬时信号以及该信号之前的若干个信号共同作用于输出信号,能够达到输入/输出呈线性特性。
3.1 伪记忆模型的建立与求解
当无记忆功放建立伪记忆模型时,首先需要进行的就是记忆深度的研究和确定。本文对记忆深度的确定问题建立了2条基本原则,分别是误差最小化原则(MEP)和操作最简化原则(SOP)。
误差最小化原则(MEP):所选取的记忆深度应为记忆深度的可选取范围,并能够使得归一化均方误差基本接近或到达该可选范围的误差最小值。
操作最简化原则(SOP):所选取的记忆深度应为记忆深度的可选取范围,并能够使得在操作实施中该记忆深度基本接近或到达可选范围的最简,即为记忆深度最小值。
依据以上2条基本原则,通过数据仿真结果,可以确定记忆深度M为3,进而可以得到伪记忆模型为:
(5)
对于该模型的使用,本文运用矩阵逆运算方法,可以简单方便地完成伪记忆模型的系数求解。
(1) 建立运算矩阵
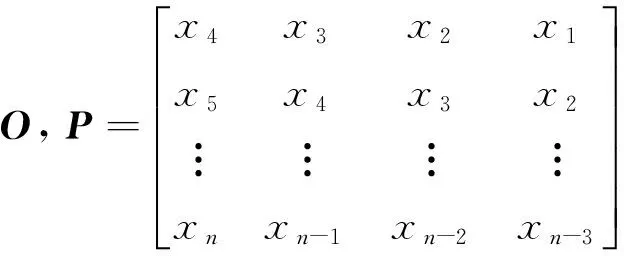
P·H=O
(6)
完成以上对模型的求解,可以得到伪记忆模型的系数值(分别如表3所示)。

表3 伪记忆模型系数值
可以得到确切系数的模型为:
(7)
(3) 依据伪记忆模型,得到的信号是否通过预失真模块的放大效果对比曲线如图3所示。
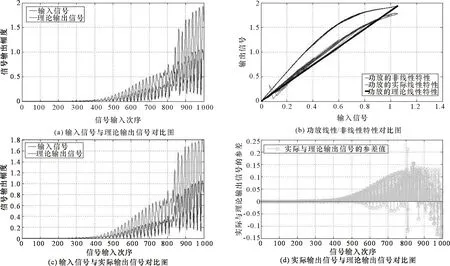
图3 通过预失真模块前后功放的放大效果对比图
(4) 将伪记忆模型进行NMSE准确度评价,得到伪记忆模型的评估值为-20.33 dB。
3.2 伪记忆深化模型的建立与求解
从对伪记忆模型的NMSE评价值可以看出,该模型的准确度相对较低,从图中也可以清晰地看出这一现象。为了进一步增强伪记忆模型的应用价值和可信度,在其基础上同时考虑输入信号的高阶多项式,从而使得考虑因素更全面、更深入。得到伪记忆深化模型[4]:
(8)
(9)
针对本问题大数据量的特点,无法一次完成计算。本文创新性地运用序贯最小二乘估计(基本流程如图4所示),给较大的数据量加上“时间标签”,人为地将全部数据作为随时间逐渐增加的数据流来处理,不必对全部数据进行批处理,从而达到对伪记忆深化模型的系数求解。
图4为求解模型系数估计量的更新过程,其中粗箭头代表了矢量处理[5]。
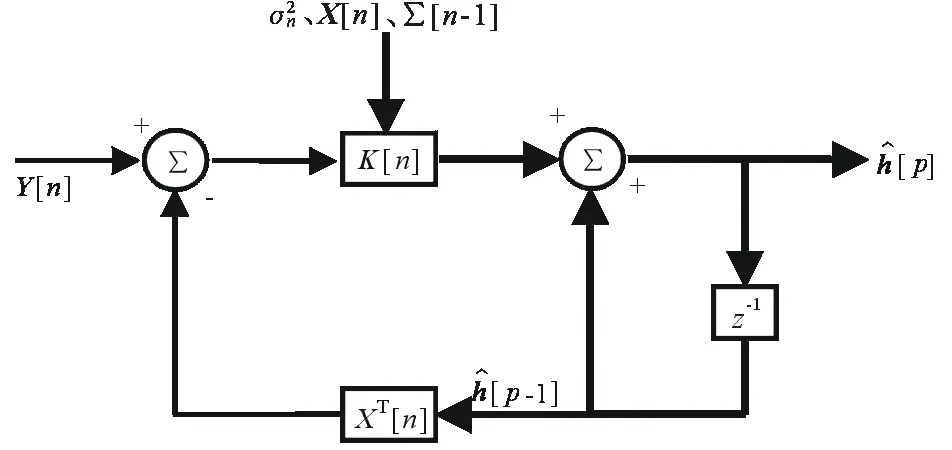
图4 序贯最小二乘估计量流程图
(1) 建立初始矩阵
设定记忆深度为M,最高阶次为K,初始时选择N个数据,则构造一个N×(MK)的矩阵:
(10)
Y[N]=[y(n)y(n+1) …y(n+N-1)]
(11)
(2) 计算批估计量

(12)
通过上式可以得出参数的估计量。
(3) 参数估计量的更新
在已知参数集的基础上,每增加一行新的数据,参数估计量进行一次更新,新的估计量在老的估计的基础上增加一个修正项。修正项随着数据的增多而逐渐下降,从而可以说明,随着数据的增加,参数的估计量越精确化。
进行参数估计量更新的运算:
(13)
(14)
Σ[n-1]=(XT[n]C-1[n]X[n])-1
(15)
(16)
通过计算,得到了记忆深度为3伪记忆深化模型的系数值如表3所示。

表3 伪记忆深化模型的系数值
依据伪记忆模型,得到信号是否通过预失真模块的放大效果对比曲线,如图5所示。
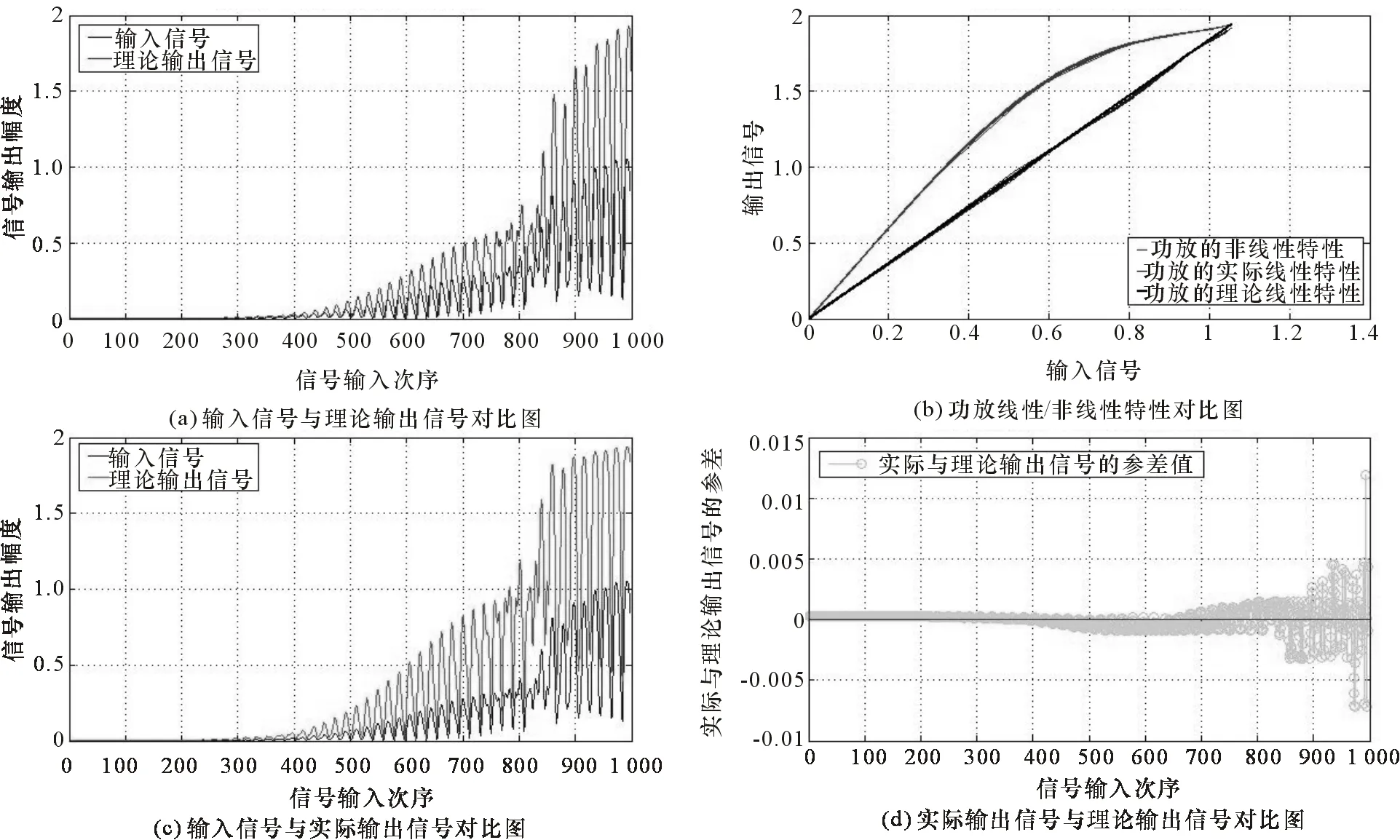
图5 通过预失真模块前后功放的放大效果对比图
将伪记忆模型进行NMSE准确度评价,得到伪记忆模型的评估值为-55.34dB。
4 结束语
本文创造性地提出了多项式拟合阶数原则,将模糊问题定量化,在一定程度上减少了阶数确定的盲目性。能够将复杂问题简单化,极大地提高了运算效率,巧妙地将有记忆功放的特性应用于无记忆功放,实现了简便的线性化特性,提高了预失真处理的效率和精度。但是,如何使模型大众化,普及到非专家化的科研工作者,进一步加强模型的方便和实用是最有意义的改进方向。
[1]RavivRaich.Orthogonalpolynomialsforpoweramplifiermodelingandpredistorterdesign[J].IEEETransactionsonVehicularTechnology,2004,53(5):1468- 1479.
[2]MorganDennisR.AgeneralizedmemorypolynomialmodelfordigitalpredistortionofRFpoweramplifiers[J].IEEETransactionsonSignalProcessing,2006,54(10):3852-3860.
[3] 罗鹏飞.统计信号处理[M].北京:电子工业出版社,2001.
[4] 陈亚勇.MATLAB信号处理详解[M].北京:人民邮电出版社,2001.
[5] 邬学军.数学建模教程[M].杭州:浙江大学出版社,2009.
Pre-distortion Mathematical Model of Memoryless Power Amplifier
HOU Dao-qi,YANG Zheng
(Electronic Engineering Institute,Hefei 230037,China)
This paper studies the nonlinear characteristic of memoryless power amplifier (PA),sets up the orthogonal basis fitting model,uses inner product method to solve the model parameters,performs the fitting research and simulation,aiming at pre-distortion processing,respectively establishes the false memory model and in-depth false memory model,adopts sequence least squares method,can solve multiple unknown parameters in multi-model conveniently and effectively,realizes the input/output linearization of power amplifier,performs the fitting simulation.
memoryless power amplifier;pre-distortion;model;false memory
2015-07-01
TN722.75
A
CN32-1413(2015)04-0056-06
10.16426/j.cnki.jcdzdk.2015.04.015

