图类{K2*Pn+2e}的边-平衡指数集

谭秋月,孙平安,徐梁立,黄立红

1.武夷学院数学与计算机系,福建武夷山354300

2.厦门大学数学科学学院,福建厦门361005

图类{K2*Pn+2e}的边-平衡指数集

谭秋月1,孙平安1,徐梁立1,黄立红2

1.武夷学院数学与计算机系,福建武夷山354300

2.厦门大学数学科学学院,福建厦门361005

研究了特殊图类的边的标号问题，根据字典乘积图概念定义了{K2*Pn+2e}这种特殊图类，并利用图结构的分解和边标号互换的方法给出了该图类的平衡指数集的准确值和证明。

边标号;边平衡指数集;{K2*Pn+2e}图类

1 引言

图的顶点和边标号问题是一个比较有趣的问题，也是图论中的热点问题之一。1992年，Lee等考虑图的顶点友好标号问题[1]。1995年，Kong和Lee提出了相对应的边友好标号问题[2]。

定义1设G=(V(G),E(G))为一个简单图，映射f为对图G所有边的一个{0,1}标号，即f:E(G)→{0,1}，∀e∈E(G)，定义f(e)=0或1，在映射f下标号为0或1的边集记为Ef(0)，Ef(1)，用ef(0)，ef(1)分别来表示此二集合的基数。由f诱导出一个对图的G部分顶点的{0,1}标号函数f*定义如下:图G中的任意一个顶点，若关联的边中标1的边数多于标0的边数时，则顶点标1；若关联的边中标1的边数少于标0的边数时，则顶点v标0；若关联的边中v标1的边数等于标0的边数时顶点v不标号。图G在f诱导出映射f*标号为0或1的顶点集分别记为Vf(0)，Vf(1)，它们的基数分别记为vf(0)，vf(1)。

定义2设f是图G的边集E(G)上的一个0、1标号函数，如果|ef(1)-ef(0)|≤1，那么就称f是图G的边-友好标号。

定义3如果f是图G的边-友好标号，若在边-友好标号f下满足|vf(1)-vf(0)|≤1，则称f为边-平衡标号。定义集合{|vf(1)-vf(0)|}，f为图G的友好标号}为图G的边-平衡指数集，记为EBI(G)，记EBI(G)中最大的元素为maxEBI(G)。

2 相关EBI(G)引理

图G的边平衡指数集没有一般的计算公式，文献[3-6]中计算了Kn×K2、路Pn、圈Cn、完全图Kn、轮Wn和n-möbius梯子的EBI(G)，并给出了一下引理：

引理1若图G的所有顶点都为奇点，则EBI(G)只包含偶数。

引理2若图G为有p个顶点的r正则图，图G存在边-友好标号f，则

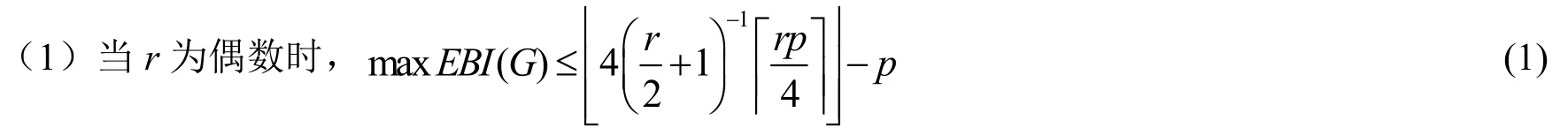
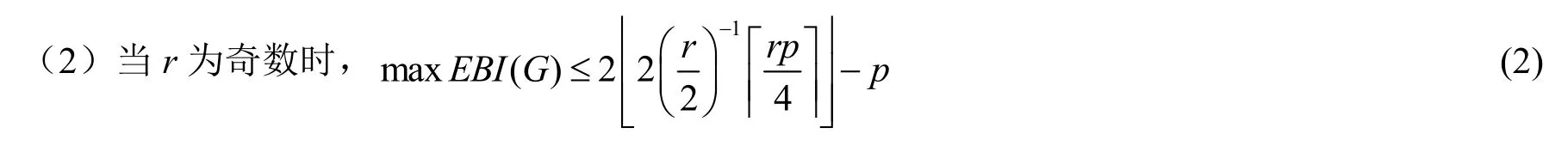
3 结论及其证明

本文所考虑的图都是有限无向简单图。一个图G对应着一个有序对(V(G)，E(G))，记G=(V(G)，E(G))，V(G)和E(G)分别表示图G的顶点集和边集，|V(G)|=p，|E(G)|=q，其他未加说明的术语和符号均引自文献[7]。首先介绍与本论文有关的图的一种运算，称为合成运算。

定义4[7]设G1=(V1,E1)与G2=(V2,E2)是两个图，G1关于G2的合成运算，称为关G1于G2的字典乘积图(lexicographic product)，记作，以为顶点集，并且以为边集组成的图。

定义5设K2=(V1,E1)是2个顶点的完全图，Pn=(V2,E2)是n(n≥2)个顶点的路图，以为顶点集，并且以,或u1=u2且(v1,v2)∈E2﹜+2e(其中为边集组成的图，称为正则图{K2*Pn+2e}(n≥2)。

可见n≥3以后，K2*Pn+2e=K2*Cn。K2*Pn+2e(n≥2)是顶点数为2n，边数为n(n+2)的(n+2)-正则图。为了证明方便，对图类K2*Pn+2e的顶点重新标定，将Pn在K2*Pn+2e中第一行顶点标号为u，u1，L，un-1，Pn在K2*Pn+2e中第二行顶点标号为v，v1，L，vn-1，且uv恰好是K2在K2*Pn+2e中的1个复制，uivi恰好为K2在K2*Pn+2e中的i+1个复制，其中i=1，2，L，n-1，如图1所示为K2*P2+2e，如图2所示为K2*P3+2e。

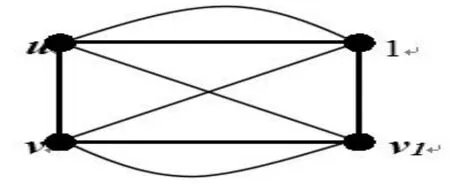
图1 正则图{K2*P2+2e}Fig.1 Canonical graph{K2*P2+2e}

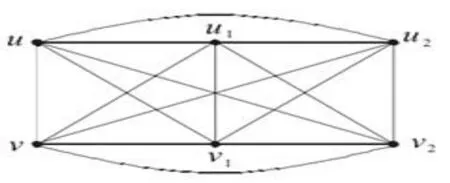
图2 正则图{K2*P3+2e}Fig.2 Canonical graph{K2*P3+2e}

通过分析图类K2*Pn+2e(n≥2)的结构，数学归纳法给出图类{K2*Pn+2e}(n≥2)的maxEBI(G)的边-友好标号，然后通过边互换的方式给出EBI(G)的所有元素，得到了以下定理：

定理1图类{K2*Pn+2e}(n≥2)的边平衡指数集为：

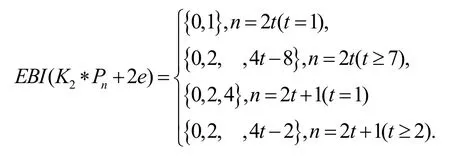
在证明过程中用f(a,b,c)表示图G在边-友好标号f诱导出的顶点标号f*中，标1的顶点数为a个，标0的顶点数为b个，不标号的顶点数为c个，显然有p=a+b+c。

证明（1）当n=2t时，p=4t，q=4t2+4t，r=2t+2。由引理2知

如下图3所示对图类{K2*P2+2e}进行边-友好标号，对顶点v的边0,1标号分类为（1001）（0011）（0101）分别对应图3中(a)(b)(c)的顶点无标号的三种，图正则且对称，0,1边互换后，得到的（0110）（1100）（1010），顶点依然无标号，EBI(G)取不到值。

在图4中，给出了图类{K2*P2+2e}的部分边-友好标号，可见|vf(1)-vf(0)|=0或者1。结合公式（3），得到图类{K2*P2+2e}的EBI(G)值为0,1，即EBI(G)={0,1}。

图3 正则图{K2*P2+2e}Fig.3 Canonical graph{K2*P2+2e}

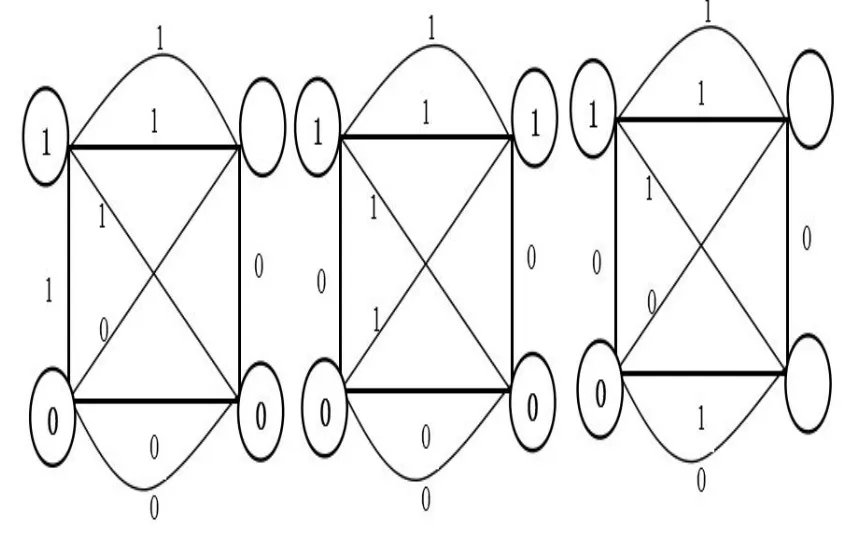
图4 正则图{K2*P2+2e}EBI(G)为0,1的部分情况Fig.4 The partial results ofEBI(G)=0,1 in canonical graph{K2*P2+2e}

当2≤t≤6时，只求出了EBI(G)的最大值

⑦当7≤t≤14时，maxEBI(G)=4t-7；当15≤t时，maxEBI(G)=4t-8。若存在边友好标号f(a,b,c)，

第一步，记顶点集A={u1，u2，L，u2t-2}，B={v1，v2，L，v2t-2}。给定边标号的方式f如下：标0的边是边uu2t-1，边uv2t-1，边vv2t-1，边u2t-1v（即u和u2t-1及u和B的所有顶点连成的边，v和v2t-1及v和A的所有顶点连成的边），边uiui+j(i=1，2，L，2t-2；j=1，2，L，t-1(mod2t-2))；其他边都标1；则ef(0)=4+4×(2t-2)+(2t-2)(t-2)=2t2+2t，因此f为边-友好标好，此时u，v，u2t-1，v2t-1相关联的边中各有2t条边标0，因此f(u)=f(v)=f(u2t-1)=f(v2t-1)=0；ui和vi相关联的边中各有k条边标0，因此f(ui)=f(vi)=1(i=1，2，L，2t-2）。在边标号的f下，|vf(1)-vf(0)|=4t-8。

第二步，通过边互换的方式得到EBI(G)中的其他元素。规定将边互换以后的边标号称为g。顶点u,v,u2t-1,v2t-1最多各有t-2条边0边变成1边而仍不改变这些顶点在g下的标号，做互换uvi←→uivi(1，2，L，t-2)，得到EBI(G)值为4t-9，4t-10，L，3t-6的K2*Pn+2e；将边互换u2t-1vi←→ui-1vi(i=2，3，L，t-1)，得到EBI(G)值为3t-7，3t-8，L，2t-4的K2*P2+2e；将边互换uiv←→uivi+1(i=t-1，t，L，2t-3)，得到图K2*Pn+2e类{K2*Pn+2e}的EBI(G)值为t-3，t-4，L，0。

（2）当n=2t+1时，p=4t+2，q=4t2+8t+3，r=2t+3。每个顶点都为奇点，所以不标号的顶点个数应该为0，f(a,b,c)=f(a,b,0)由引理2知，

（i）当n=3，t=1时，p=4t+2=6，q=4t2+8t+3=15，G={K2*P3+2e}，maxEBI(G)≤4，由引理1可知，EBI(G)值只为偶数，又因为|vf(1)+vf(0)|=6，且f为边友好标号必须满足|ef(1)-ef(0)|≤1，所以EBI(G)只可能为0，2，4。

若f为边友好标号，则f(a,b,0)只可能为f(3,3,0)，f(4,2,0)，f(5,1,0)。如图5（a）-（c）所示，给出图类{K2*P3+2e}的EBI(G)为0,2,4的情况，所以EBI(G)={0，2，4}。如图5（d）所示，f(6,0,0)是不可能的。|vf(1)+vf(0)|=6，但是|ef(1)-ef(0)|≤2，而且每个标1的顶点关联标号为0的边都达到了临界值。所以EBI(G)不可能为6。

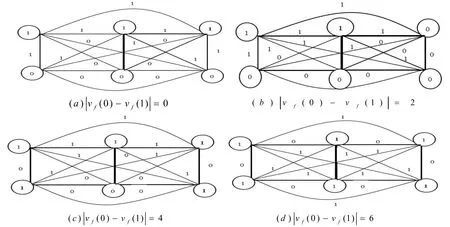
图5 正则图{K2*P3+2e}的EBI(G)为0,2,4的部分情况Fig.5 The partial results ofEBI(G)=0,2,4 in canonical graph{K2*P3+2e}

（ⅱ）当n=5，t=2时，p=4t+2=10，q=4t2+8t+3=35，G=K2*P5+2e，maxEBI(G)≤8，由引理1可知，EBI(G)值只为偶数，又因为|vf(1)+vf(0)|=10，且f为边友好标号必须满足|ef(1)-ef(0)|≤1，所以EBI(G)只可能为0,2,4,6,8。若f为边友好标号，则f(a,b,0)只可能为f(9,1,0),f(8,2,0)，f(7,3,0)，f(6,4,0)和f(5,5,0)。如图6（a）-（d）所示，给出图类{K2*P5+2e}的EBI(G)为0,2,4,6的部分情况，所以EBI(G)=﹛0,2,4,6﹜。如图6（e）所示，要满足|vf(1)+vf(0)|=10，|vf(1)+vf(0)|=8且|ef(1)-ef(0)|≤1，如果f(a,b,0)=f(9,1,0)时，每个标1的顶点关联标号为0的边都达到了临界值，f(9,1,0)取不到图，所以EBI(G)不可能为8，图类{K2*P5+2e}的EBI(G)只可能为0,2,4,6，EBI(G)={0,2,4,6}。在图6中，由于边太多，只标0边，没有标记的边标号都为1。

图6 正则图{K2*P5+2e}的EBI(G)为0,2,4的部分情况Fig.6 The partial results ofEBI(G)=0,2,4 in canonical graph

当t≥3时，，所以maxEBI(G)=8t-(4t+2)=4t-2。

第一步，记顶点集A={u1，u2，L，u2t}，B={v1，v2，L，v2t}。给定边标号的方式f如下：标0的边是边uv，u和B的所有顶点连成的边，v和A的所有顶点连成的边，边uiuj(i=1，2，L，2t；j=i+1，i+2，L，i+t(mod2t))，其他边都标1。

第二步，通过边相互交换的方法得到EBI(G)中的其他元素。规定将边互换以后的边标号称为g。顶点u，v最多各有t-1边标0边变成标1边而仍不改变顶点u，v在g下的标号，做边的相互交换uvi←→uivi(i=1，2，L，t-1），且由引理1知，得到图类{K2*Pn+2e}的EBI(G)值只能为偶数4t-4，4t-6，L，2t；做边的相互交换vui←→uivi(i=t，t+1，L，2t-2)，得到图类{K2*Pn+2e}的EBI(G)值为2t-2，2t-4，L，2；将边uiu2t由标0边变成标1边，此时ef(0)=4t2+4t+2，可见f仍为边-友好标好，但此时f(u2t)=0，f(u)=0，因此得到图类{K2*Pn+2e}的EBI(G)值为0。

4 结语

利用对图组顶点序列号特征，递归到整个图形，进而给出了图类{K2*Pn+2e}边-平衡指数集。

在计算图的边平衡指数集方面，本文虽然解决了图类{K2*Pn+2e}的边平衡指数集，但花费了较多时间尝试着去研究是否存在某种等价定义更通用化更一般化的转化方式使得计算图的边平衡指数集更为简单？目前没有更好的结果，这一方面可以继续更深入研究。另一方面，读者也可以构造和寻找更多的具有良好性质的对称的图类，给出这些图类的顶点和边的平衡指数集，本文中标号函数的设计方法为其他合成图、正则图的研究提供了很好的思路借鉴，所证结果为图论和编码理论提供了重要的公式和数据。

[1]Lee SM,Liu AC,Tan SK.On balanced graphs[J].Congr.Numer.,1992,87:59-64

[2]KONG MC,LEE SM.On edge-balanced graphs[J].Graph Theory,Combinatoric and Algorithms,1995(1):711-722

[3]Kong E,Lee SM,Raridan C.On the edge-balanced index sets of product graphs[J/OL].J.Indones.Math.Soc. http://arxiv.org/abs/1103.4994,2011-03-25

[4]Wang TM,Lin CM,Lee SM.On edge-balanced index sets of regular graphs[A].The 26th Workshop on Combinatorial Mathematics and Computation Theory,218-223

[5]Krop E,Sikes K.On the edge-balanced index sets of complete bipartite graphs[J/OL].Arxiv.http://arxiv.org/abs/1106.1085,2011-06-06

[6]Chopra D,Lee SM,Su HH.On edge-balanced index sets of wheels graphs[J].Int.J.Contemp.Math.sciences,2010,5(53):2605-2620

[7]哈拉里F.图论[M].李蔚萱译.上海:上海科学技术出版社,1968:26

[8]谭秋月.若干图类的平衡指标集[J].昆明理工大学学报:自然科学版,2014,39(12):136-140

The Edge-balanced Index Sets of the Graphs{K2*Pn+2e}

TAN Qiu-yue1,SUN Ping-an1,XU Liang-li1,HUANG Li-hong2
1.Department of Mathematics and Computer/Wuyi College,Wuyishan354300,China
2.College of Mathematics Science/Xiamen University,Xiamen361005,China

In this paper,the edge-balance index for some particular graphs was studied.According to the lexicographic product graph concept,the families of the graphs{K2*Pn+2e}were defined and to provide the accurate value and proof for the exact balance index set of the families of the graphs{K2*Pn+2e}with the interchange between the decomposition of the graph structure and the edge label.

Edge label;edge-balanced index set;families of the graph{K2*Pn+2e}

O157.5

:A

:1000-2324(2015)06-0927-05

2014-04-23

:2014-05-06

福建省自然科学基金项目(2013J05006);若干特殊图类的边-平衡指标集研究(XL201409);福建省大学生创新创业训练计划项目(201510397029);若干图类友好标号问题的研究(JA15513)

谭秋月(1980-),女,硕士研究生,讲师,研究方向为图论、离散数学.E-mail:tqyspa@163.com