汽车座椅电机蜗轮蜗杆传动机构的仿真分析

李新华，刘 洋，陈泽宇

LI Xin-hua, LIU Yang, CHEN Ze-yu

（中南林业科技大学 机电工程学院，长沙 410000）

0 引言

随着汽车行业的蓬勃发展，汽车座椅电机越来越受到汽车制造商的重视，不仅要求电机质量轻，体积小，寿命长，对电机的噪音和振动也提出了很高的要求。电机的蜗轮蜗杆传动机构是影响座椅使用性能的主要因素，利用虚拟样机技术研究这种机构可以有效地缩短开发周期和降低制造大量样品的成本，还可以为其他设计任务以及物理样机的试验提供基础和参考依据。针对该传动机构所进行的运动特性和动态特性的理论研究和分析，具有重要的实际应用意义。

1 汽车座椅电机蜗轮蜗杆传动机构的基本参数和材料性能

该机构的蜗轮为聚甲醛[1]（POM）材料，蜗杆由45钢制造而成。蜗轮蜗杆的齿形基本参数和材料性能如表1所示。

表1 蜗轮蜗杆的齿形基本参数和材料性能

2 汽车座椅电机蜗轮蜗杆传动机构三维模型的建立

在Pro/E中分别对蜗轮和蜗杆进行三维建模，并按照中心距完成装配。图1是该机构的装配简图，图中蜗杆是在实际运动过程中，与蜗轮啮合的部分。该机构蜗杆作为驱动件，蜗轮作为从动件。

图1 蜗轮蜗杆传动机构装配简图

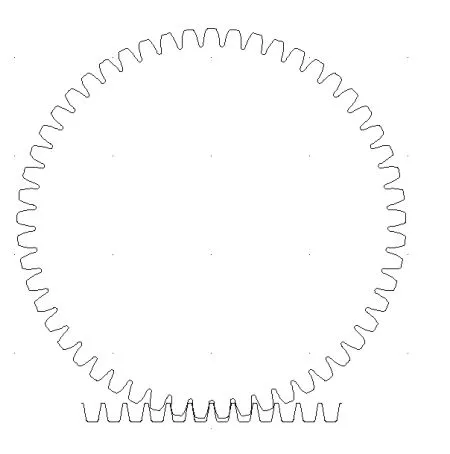
图2 蜗轮蜗杆传动机构啮合示意图

图2 是利用CAXA电子图板[2]生成该机构的齿廓啮合示意图，可见啮合情况很好。

3 汽车座椅电机蜗轮蜗杆传动机构虚拟样机的建立

3.1 三维实体模型导入至ADAMS

把Pro/E中装配好的模型保存为标准转换数据*x.t格式[3]文件，在ADAMS中通过file import导入到ADAMS/View模块，然后定义重力的方向和重力加速度的大小，定义各个部件的质量和密度等材料属性。

3.2 定义运动副

利用ADAMS中的Connectors功能块对各个部件添加运动副。在蜗轮和地面之间定义转动副，转动中心为蜗轮的物理中心；在蜗杆和地面之间定义转动副，转动中心为蜗杆的物理中心；在蜗轮和蜗杆之间添加齿轮副[4]，并确定啮合点的位置。

3.3 选取ADAMS动力碰撞参数[5]

为了使虚拟样机模型更符合物理样机模型，需要在蜗轮和蜗杆之间定义动力碰撞接触力。在ADAMS中有两种不同的接触力计算方法，一种是Impact法，另一种是Restitution法。本文采用Impact法，其函数定义为：

其中，STEP是阶跃函数，q0是两物体之间的初始距离，q是两物体发生碰撞过程中的实际距离，q0-q表示碰撞过程中的变形量。

函数定义式表明：当q≥q0时，两物体不发生碰撞，即F_Impact=0；当q＜q0时，两物体发生碰撞，碰撞力的大小与刚度系数K、变形量q0-q、碰撞指数e、阻尼系数C和阻尼完全作用时变形距离d有关。

刚度系数K取决于两物体的材料和结构，根据Hertz碰撞理论[6]，可由下式计算得到：

式中，R和E分别由下式计算得到：

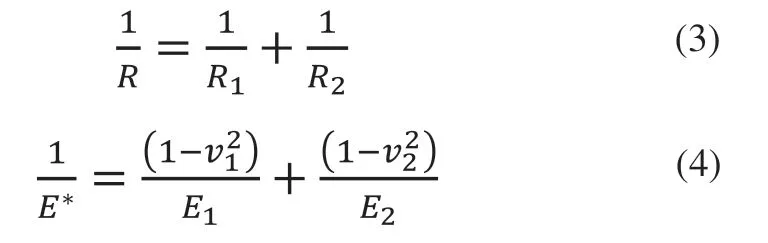
式(3)和式(4)中，R1和R2分别是蜗轮和蜗杆接触点的当量半径，由于齿高和分度圆半径相比较小，因此变动范围不大，可近似用分度圆上的值来代替，这样的近似误差很小[7,8]。E1和E2分别是蜗轮和蜗杆材料的杨氏模量，E1=203GPa，E2=3.1GPa。v1和v2分别是蜗轮和蜗杆材料的泊松比，v1=0.25，v2=0.39。

根据式（2）可得蜗轮蜗杆碰撞的刚度系数为：K=3600N/mm。蜗轮和蜗杆之间进行了润滑脂处理，动摩擦因数取0.05，静摩擦因数取0.08。

3.4 定义驱动件运动方程

在驱动件蜗杆上施加转速驱动。该汽车座椅驱动电机蜗杆的最高转速为36r/min，即216º/s。为了使转速缓慢增加而不出现突变，定义转速的STEP函数[9]为STEP(time,0,0D,0.3,216D)，即蜗杆转速在0.3s内从0缓慢增加到216º/s，其中time是时间变量。图3是驱动件运动方程的曲线图。

图3 驱动件（蜗杆）转速曲线图

3.5 定义从动件负载方程

由于该虚拟样机是刚体模型，在进行模拟时需要施加负载[6]，因此在蜗轮上添加一个恒定的静态负载T=24N·m。为了使负载缓慢增加，提高仿真效果，在蜗杆转速平稳后，定义静态负载方程为STEP(time,0.3,0, 0.5,24000)，即静态负载在0.3s～0.5s内从0缓慢增加到24000N·mm。

至此，利用ADAMS完成了该机构的虚拟样机模型的建立如图4所示。

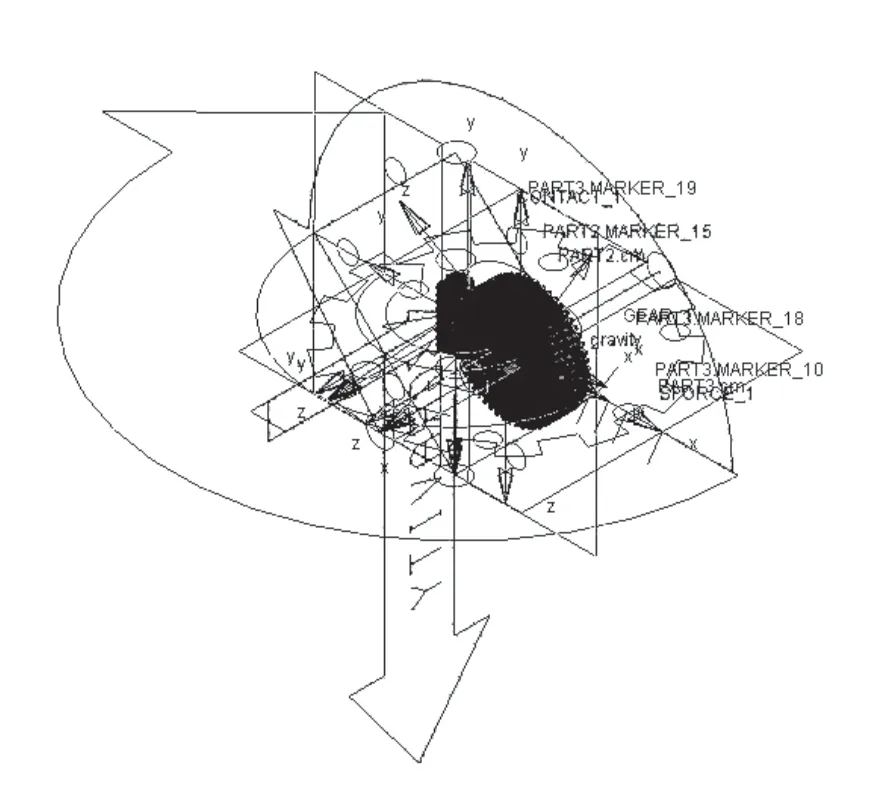
图4 虚拟样机模型

4 汽车座椅电机蜗轮蜗杆传动机构仿真结果分析

4.1 运动学仿真结果分析

取仿真时间为0.5s，步长设定为0.005s。图5是蜗轮的转速随时间的变化曲线，可见在0～0.3s内，蜗轮的转速从0缓慢增加到4.075º/s。图3中蜗杆的转速在0～0.3s内从0缓慢增加到216º/s，据此可以求出该机构的传动比为i=216/4.075=53.01，而该机构的理论传动比为蜗轮蜗杆的齿数比，即53/1=53，说明转速大小与理论上的传动比非常吻合，验证了虚拟样机的正确性。

图5 从动件（蜗轮）转速曲线图

4.2 动力学仿真结果分析

取仿真时间为2 0 s，步长设定为0.0 2 s。利用ADAMS/ProProcessor模块分别得到蜗轮蜗杆沿x方向、y方向上的啮合力CONTACT1的时域图和频域图。以从动件蜗轮作为对象，x方向对应径向力，y方向对应切向力。图6、图7分别是两个力随时间t变化的时域图和随频率f变化的频域图。

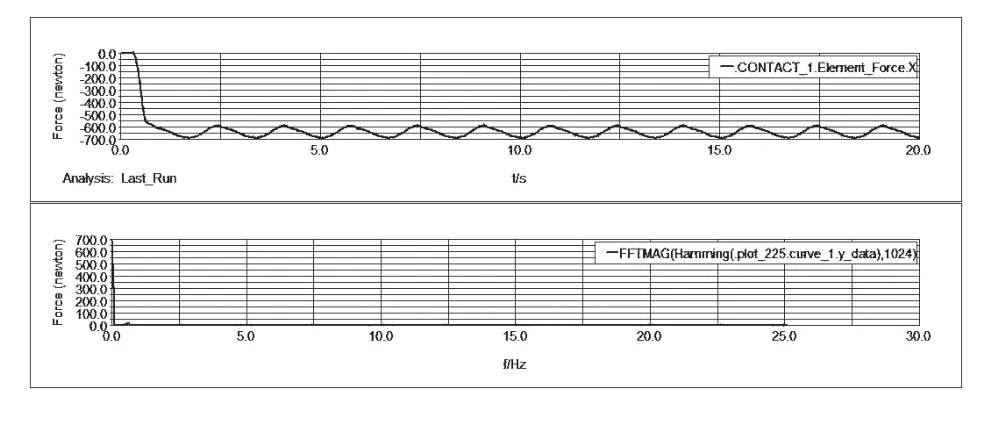
图6 x向啮合力（径向力）时域和频域图

图7 y向啮合力（切向力）时域和频域图

从时域图中可以看出，啮合力在0～0.15s内没有变化，这是因为蜗轮和蜗杆尚未接触，啮合力为0。0.15s～0.3s内，啮合力逐渐增大，这是由于对蜗杆进行了阶段性的加载。0.3s以后，随着加载的稳定，啮合力的波动减小且趋于稳定均值的状态，这是由于蜗轮和蜗杆的周期性碰撞引起的，表明蜗轮和蜗杆啮入啮出情况很好，传动连续，无明显冲击[11]，体现了蜗轮蜗杆传动的特点。

从频域图中可以看出，啮合力均在0.6Hz时达到最大值，因此该机构的啮合频率为0.6Hz。根据齿轮啮合频率理论计算公式[12,13]f=Z·n/60（Z是齿数，n是转速），可求得该机构的啮合频率为0.599，相对误差为0.17%，两者基本吻合，可见从频域上说明了仿真的可信度，同时为驱动电机在实际工作情况下必须规避的频率范围和动态特性优化设计[14]提供了理论依据。

5 结论

对汽车座椅电机的蜗轮蜗杆传动机构进行了仿真分析。利用Pro/E建立起该机构的三维模型，导入到ADAMS后，添加运动副和碰撞力，完成虚拟样机的建立。通过动态仿真，得到了从动件蜗轮的转速以及该机构的传动比，并且与理论计算值相比误差很小。同时还得到了蜗轮和蜗杆的啮合力在xy两个方向上的时域图和频域图，确认了该机构的啮合频率。这些仿真结果都说明了虚拟模型的可行性和可信度，从而可以为该机构以及驱动电机的进一步优化设计提供理论依据。

[1] 樊新民,车剑飞.工程塑料及其应用[M].北京：机械工业出版社,2006.

[2] 董振珂.计算机绘图CAXA电子图板V2[M].北京：化学工业出版社,2007.

[3] 余波,王家序,黄春美,官浩.基于ADAMS的孔销式少齿差行星减速器的设计与仿真分析[J].机械设计与研究,2013,29(3)：23-27.

[4] 葛正浩.ADAMS2007虚拟样机技术[M].北京：化学工业出版社,2010.

[5] 李长群,贾长治,武彩岗.基于虚拟样机技术的齿轮啮合动力学仿真研究[J].系统仿真学报,2007,19(4)：203-206.

[6] 危自强,王家序,肖科,李敏.基于ADAMS的新型滤波器传动件的动力学仿真研究[J].机械传动,2010,34(6)：1-4.

[7] 龙凯,程颖.齿轮啮合力仿真计算的参数选取研究[J].计算机仿真,2002,19(6)：87-88,91.

[8] Kahraman K.Planetary Gear Train Dynamics[J].Journal of Mechanical Design,1994,116(9)：712-720.

[9] HUANG Zeping,MA Jisheng,WU Dalin. Simulation study on contact stress of gear tooth[J].Journal of Mechanical Transmission,2007,31(2)：26-28.

[10] 濮良贵,纪名刚.机械设计[M].北京：高等教育出版社,2001.

[11] 孙伏.基于虚拟样机技术的渐开线少齿数齿轮传动性能分析[J].机械设计与制造,2012,(2)：154-155.

[12] 谭智,周新民.基于ADAMS的齿轮变速箱动态特性仿真分析[J].林业机械与木工设备,2009,37(11)：31-33,36.

[13] 华顺刚,余国权,苏铁明.基于ADAMS的减速器虚拟样机建模及动力学仿真[J].机械设计与研究,2006,22(6)：47-52.

[14] 王雁.基于ADAMS的变速箱齿轮的运动学和动力学仿真[J].制造业自动化,2011,(5)：111-112.