基于ADAMS+MATLAB的移动焊接机器人运动仿真
王 帅,张 华,叶艳辉
WANG Shuai, ZHANG Hua, YE Yan-hui
(南昌大学 江西省机器人与焊接自动化重点实验室,南昌 330031)
0 引言
随着工业的不断发展,焊接技术作为基础技术之一,对于航天航空、船舶制造、特种工业制造等起着决定性的作用。人工焊接作为传统焊接手段,受到环境恶劣、生产率低下等的制约。随着自动化水平不断发展,自动化焊接设备被引入到工业制造中。其中,移动焊接机器人作为典型的焊接机器人,拥有可靠稳定、保证焊接质量等优点,被广泛应用到船舶焊接中。
由于移动焊接机器人是一个复杂的被控对象,移动机构的机械误差、焊接过程中的扰动、轮胎与地面之间的摩擦等因素都会使得机器人产生偏差,使其运动特性受到影响。本文针对狭小空间内平面焊缝自动化焊接的移动焊接机器人进行了建模,讨论了其运动学模型以及跟踪偏差,最后利用ADAMS与MATLAB联合仿真技术对于虚拟样机进行仿真,以指导物理样机焊接实验,减少实验次数,降低研发成本。
1 移动焊接机器人结构建模
如图1所示,为移动焊接机器人结构图,采用轮式移动平台,具有两个独立自由度,配合万向球构成三点支撑,两轮以差速形式使得移动平台转动,当两驱动轮以同速反向运动时,移动平台可完成转弯半径为零的圆周运动。根据焊接精度要求,选取十字滑块作为二维精确运动平台作为主要跟踪机构,其由两相互垂直的滚珠丝杠机构组成,能在平面内任意往复运动,具有运动平稳、精度高和可靠性好等特点。
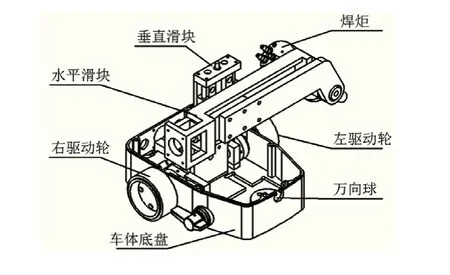
图1 移动焊接机器人结构
焊接自动化系统中最重要的问题是焊缝跟踪与实时控制。因此,焊接传感器决定了移动焊接机器人的焊接跟踪精度。本移动焊接机器人选用旋转电弧传感器作为实时传感。电弧传感不受弧光、磁场、飞溅等因素干扰,焊炬与传感器制为一体,使得检测点与焊接点统一,保证了检测的实时性。其中旋转电弧传感具有旋转频率高、跟踪精度好,且其旋转半径和速度可调等优点,更加适用于狭小焊接环境。
2 移动焊接机器人运动学模型及偏差分析
移动焊接机器人是一个空间内多自由度模型,所以其在空间内运动学计算非常复杂。为了实现移动焊接机器人的运动仿真,必须建立其数学模型,该模型也是研究其控制算法的基础。
如图2所示,为移动焊接机器人焊接跟踪模型。简化模型,假设移动焊接机器人为刚性结构,驱动轮与地面为刚性接触,且做纯滚动,将其建立在笛卡尔平面坐标下。

图2 移动焊接机器人焊接跟踪模型
定义点A为移动焊接机器人移动中心点,焊接初始位置焊接点h具移动中心点距离为L,L为变量,由水平滑块所走位移决定,即取决于水平驱动步进电机的脉冲个数。驱动轮直径为D,驱动轮外侧到机器人移动中心点距离为t。定义焊缝中一点C为焊接参考点,C点与h点之间行程焊接偏差向量车体纵轴线与X轴正方向夹角为φ,焊缝在C点切线方向与X轴正方向夹角为φc。
2.1 运动学方程
由机器人运动学方程可知,当机器人受到m个约束时,在n维广义坐标P=[P1,…,Pn]T中可用下式表达:
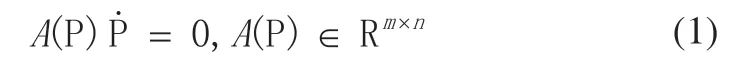
由于移动焊接机器人的运动学模型为非完整约束,在此条件下式(1)中:

式(2)中J(P)为一个n×(n-m)矩阵,K为速度矢量,且满足:

非完成约束移动焊接机器人位置的移动中心点在笛卡尔坐标中为A(xa,ya),其可定义为向量形式:
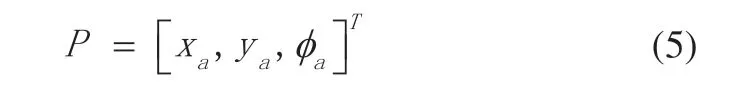
根据假设,驱动轮与地面为刚性接触,且做纯滚动,不发生滑动,式(1)中A(P)可用式(6)表达:

则根据式(3)可推出:

对于左右两驱动轮的角速度ω1、ω2与速度矢量的关系式为:

如图2所示,在笛卡尔坐标系下,可由移动焊接机器人移动中心点A(xa,ya,φa)推导出机器人执行末端旋转电弧传感器实时焊接点h(xh,yh,φh)的运动学方程:

对上式求导即可得出速度方程:
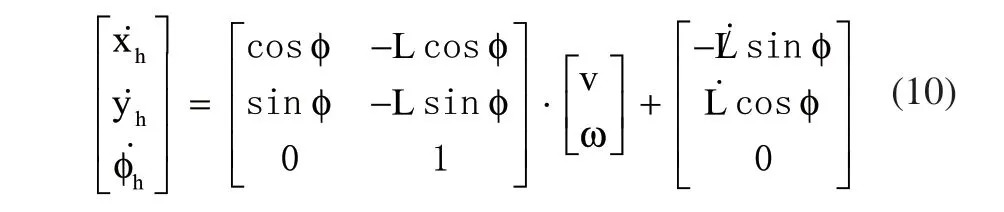
2.2 焊接偏差计算
建立焊缝中一参考点C(xc,yc,φc),并在移动焊接机器人参考坐标系中得出其速度矩阵:
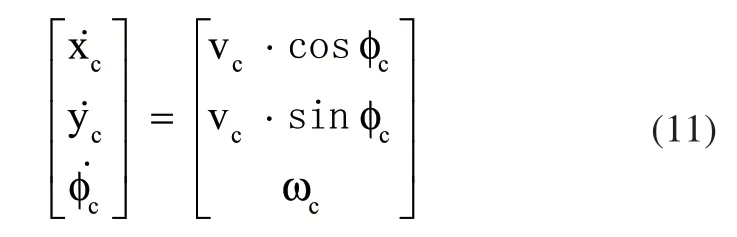
图2中定义了偏差矢量e,则计算得出移动焊接机器人在跟踪平面曲线时的偏差矢量e表示为:

3 建立虚拟样机
ADAMS是美国MDI公司研制的集建模、求解、可视化技术为一体的虚拟样机软件,是世界上使用最广泛的机械系统仿真分析软件。可真实地仿真复杂机械系统的运动过程。设计移动焊接机器人在虚拟样机中进行试验,直到获得优化的工作性能,大大减少了昂贵的物理样机制造和实验次数,提高了设计成功率。
由于ADAMS自身建模能力并不强大,因此借助CATIA建模功能,而Simdesigner是CATIA与ADAMS软件之间的接口模块,可实现二者的无缝连接,利用Simdesigner添加相应的运动约束,再导入ADAMS中,可保证模型的仿真精度。移动焊接机器人是一个复杂机械系统,对其仿真需要大量的计算工作,为了减少计算机计算量,需要对整体移动焊接机器人进行简化,删去螺纹、过渡圆弧等,将其中不发生相对运动的部件进行合并固定,图3为简化后的虚拟样机模型。

图3 虚拟样机模型

图4 弯曲焊缝轨迹
为了验证模型的正确性,对模型进行轨迹仿真。首先对垂直滑块不施加驱动,对两驱动轮和水平滑块分别添加驱动参数。左右两轮分别为180°/s。水平滑块驱动函数为:STEP(time,0,0d,1,-3600d)+STEP(time,1,0d,2,3600d)+STEP(time,2,0d,3,-1800d)+STEP(time,3,0d,4,1800d)。进行仿真后,得出弯曲焊缝轨迹如图4所示,可知此焊接移动机器人模型正确并可完成各种平面运动轨迹。
4 联合仿真
移动焊接机器人本身是一个复杂的机械系统,而焊接过程中的焊缝跟踪又需要复杂的控制系统作为支撑,ADAMS虽然功能强大,但要做到对复杂机械系统进行准确控制,ADAMS自身很难完成。所以本文采用ADAMS与MATLAB联合仿真技术对移动焊接机器人的移动平台进行控制仿真,以获得平台运动性能,为后期控制算法提供依据。
4.1 仿真原理
ADAMS和MATLAB之间的通讯是依靠状态变量进行数据传输的,需建立一组状态变量作为输入和输出,其输入输出关系如图5所示。
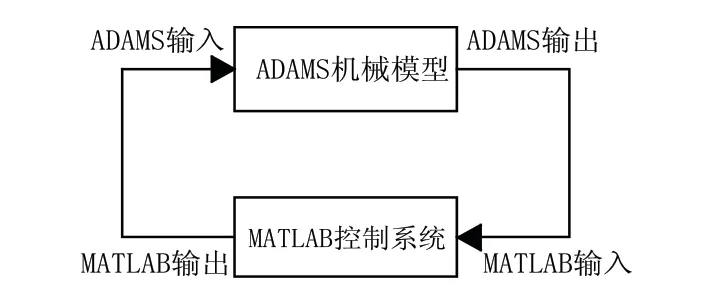
图5 联合仿真输入输出关系
4.2 仿真系统建立
对于移动焊接机器人移动平台的控制,输入必须为力矩,所以建立左右两轮的驱动力矩作为输入状态变量,运用ADAMS中VARVAL函数,控制状态变量实时返回控制力矩的值。设置两轮转速作为输出状态变量,转速单位统一为度/秒。
当对移动平台驱动轮施加同样力矩时,由于移动焊接机器人为非对称结构,使得机器人在行走方向上左轮支反力大于右轮,导致移动焊接机器人行走轨迹不为一条直线。在MATLAB中建立控制系统直接控制两轮转速,消除由于机构原因而带来的行走偏差,可进一步提高焊接跟踪精度
采用PID控制,在MATLAB中建立驱动轮稳速闭环系统,定义反馈量为左右两轮的转速,输入量为一常值与反馈转速的差值,输出量为驱动扭矩。建立闭环系统后的控制模型如图6所示。控制系统中adams_sub为移动焊接机器人机械系统模型。
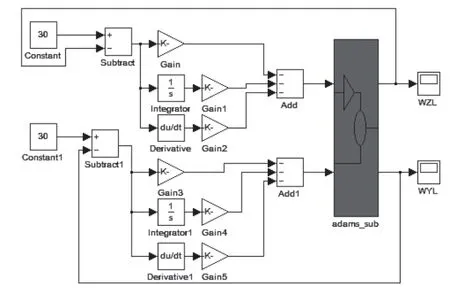
图6 速度仿真控制模型
经过多次仿真实验后,得到合理左右两轮PID控制参数分别为:KP=3,KI=800,KD=100,设定两轮转速均为30°/s,移动焊接机器人两驱动轮速度响应曲线如图7(a)、7(b)所示,由曲线可知,采用PID控制可仿真出移动焊接机器人驱动轮的转速控制特性。
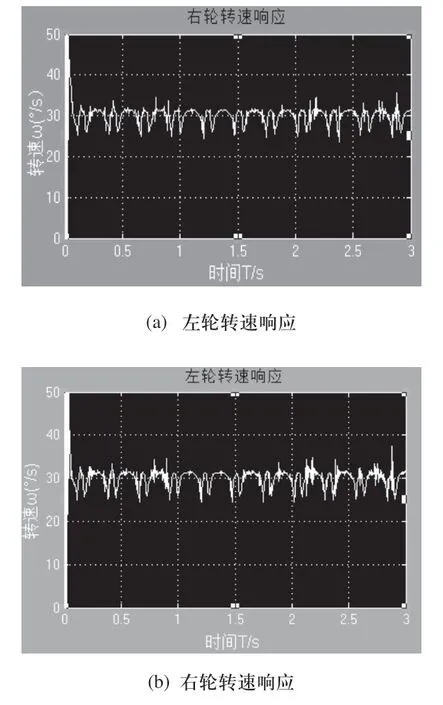
图7 左右转速响应
如图8所示,为根据仿真进行的物理实验,实验参数为焊接电流200A,电压25V,轮子移动速度40cm/min, 焊丝直径1.2mm,保护气体(Ar)80%+(CO2)20%, 保护气流量15L/min,母材的厚度为6mm。

图8 直线焊接实验结果
5 结论
1)本文针对狭小空间内平面焊缝自动化焊接的工况,建立了移动焊接机器人平台,在笛卡尔平面坐标下建立了移动焊接机器人数学模型,并针对弯曲焊缝焊接轨迹进行了运动学方程的建立和偏差计算,为其控制算法提供理论依据。
2)利用虚拟样机技术在ADAMS中建立移动焊接机器人虚拟样机,并进行了轨迹仿真,验证了模型的正确性,证明了移动焊接机器人可完成平面内焊缝焊接工作。
3)对移动焊接机器人移动平台进行了ADAMS+MATLAB联合仿真,根据移动焊接机器人结构特点,建立出其驱动轮速度控制模型,并利用PID控制进行仿真得出了其控制响应曲线,利用算法消除了由于机构特点而带来的行走偏差,为物理样机实验提供了理论依据。最后进行了实验,实验表明修正由于机构原因而带来的行走偏差可进一步提高焊接跟踪精度。
[1] 沈红芳,郑建荣.ADAMS在弧焊机器人运动学中的仿真分析和应用[J].机械设计,2004,21(12):50-52.
[2] 于殿勇,钱玉进.基于ADAMS动力学仿真参数设置的研究[J]. 计算机仿真,2006,23(9):103-107.
[3] 易声耀,潘存云.一种新型移动平台动力学仿真与试验研究[J]. 机械设计与研究,2007,23(2):55-59.
[4] 卞向娟,龚友平,陈国金.焊接机器人的虚拟样机设计与仿真[J]. 机械设计,2008,25(4):27-29.
[5] 毛志伟.旋转电弧传感移动焊接机器人机构设计与仿真[D].南昌:南昌大学,2007.
[6] 符娅波,边美华,许先果.弧焊机器人的应用与发展[J].热加工工艺,2006,35(11):79-81.
[7] 刘晋霞,胡仁喜,康士廷,等.ADAMS2012虚拟样机从入门到精通[M].北京:机械工业出版社,2013.
[8] 游世明,陈思忠,梁贺明.基于ADAMS的并联机器人运动学和动力学仿真[J].计算机仿真,2005,22(8):181-185.
[9] 张华,王海东,徐建宁,等.基于旋转电弧传感的新型轮式自主移动焊接机器人系统[J].机器人,2003,25(6):536-538,553.

