某发动机双边装配线的再平衡问题研究
杨红光,胡小锋,张亚辉
YANG Hong-guang, HU Xiao-feng, ZHANG Ya-hui
(上海交通大学 机械与动力工程学院,上海 200240)
0 引言
当前,我国装备制造业正处于高速发展时期,产品更新换代、技术革新的速度日益加快。但是,在原有装配线上导入新产品,应用新技术或新工艺,将会破坏原有装配线的平衡,使得装配线频繁出现阻塞和饥饿现象,难以高效、稳定地运行,进而导致产品制造成本的急剧上升。因此,装配线再平衡问题的研究具有理论与现实意义。Emanuel亦指出在装配线上的大量实际问题所针对的正是已经应用于生产的装配线,需要的是进行再平衡研究而非平衡,并指出装配线再平衡意义深远,应该给予重视[1]。
近几年,装配线再平衡问题受到越来越多企业和研究人员的关注。Ramirez等针对产品特征变动引起的再平衡问题进行了研究,以系统产出为目标,并应用遗传算法进行求解[2]。Corominas等针对夏季雇佣临时工人来增加产量的再平衡问题,给定再平衡后的节拍时间,以最小化临时工人数量为目标创建模型并进行求解[3]。Gamberini等针对采用新工艺的再平衡问题,以产品装配成本和再平衡前后装配线相似程度为目标,提出了一个多准则的单程启发式算法来求解该问题[4],之后,又针对该问题创建了一个多重单程启发式算法[5]。杨才君等[6~8]、Oliveira等[9]、Zhu等[10]也分别针对混装线的再平衡问题进行了一定的研究。目前,双边装配线广泛应用于大型产品的生产,如发动机和装载机等,因为它可以提供一些单边装配线不具备的优点[11],但对于双边装配线的再平衡问题至今并未有公开发表的研究成果。

图1 发动机装配线布局图
本文以某发动机双边装配线为例,针对其实际生产中频繁出现阻塞和饥饿现象,产量难以达到预期要求等问题,首先对装配线瓶颈周围部分装配工艺进行重新划分,然后以最小化平滑指数为目标,充分考虑设备和空间等约束,通过启发式算法进行任务调整,以提高装配线效率。
1 某发动机装配线的再平衡问题
该发动机装配线的布局如图1所示,S1、S2、…、S22为装配线的工作站编号,P1、P2、…、P31为工位编号,工序1、2、…、78为图中对应工位所要完成的装配作业,如{1,2,3,4}即为工位P1上执行的任务集合。表1为工序对应的信息统计表。

表1 发动机工序信息统计表
在实际生产中,该装配线的日产量大约维持在63台左右,无法满足日产量75台的预期要求。通过对装配线的运行情况进行分析,可以发现,该装配线并没有固定的节拍时间,一个工位完成后,工件移动到下一个工位。若将要移动到的工位上仍在装配,该工件即必须等待,即表明装配线出现阻塞现象;若工件移动到下一个工位时,上一个工位的装配作业还未完成,则称装配线出现饥饿现象。观察发现,装配线的工作站S1、S2、…、S17频繁出现阻塞现象,工作站S20、S21、S22频繁出现饥饿现象,而工作站S18和S19几乎一直处于较忙碌的状态。由于工作站S17操作完成后,需要离线移动到工作站S18,而移动设备要求,移动前所要求的工序任务必须完成,移动后所要求的工序任务也不能前移。因此,考虑对工作站S18、S19周围的装配工艺进行重新划分,即将工作站S18、S19上部分操作任务在满足约束的情况下调整到工作站S20、S21、S22,以减少阻塞和饥饿现象,提高系统产出。
对工作站S18、S19周围的装配工艺进行分析。工序70为各管路油管安装,由于设计到较多的高压及低压油管,密封要求高,精度要求高,而且装配步骤繁琐,所以装配速度较慢。然而考虑到这些油管并非都要按照顺序安装,其中一部分油管可以独立安装而不和其他油管干涉,且油管安装不受工装位置约束,因此将该任务分割成工序70及79这两项。任务73为燃油滤清器及线束1安装,由于是安装两个不同的零部件,因此可将其分割成73和81这两项任务。此外还可将步装工序从任务81中剥离。任务78为检查,是最终对于发动机装配质量外观的一个检查,包括漏装检测,扭矩检测等,涉及到发动机的左右两侧。由于检查工序不需要特殊的工装器具,将其分为左右两个任务78和80。
装配工艺重新划分后,工序信息变动情况如表2所示,工作站{S18,S19,...,S22}的布局及任务分配情况如图2所示。在任务再分配过程中需注意的是:1)由于检测设备的布置要求,工序78和工序80必须分配在最后一个工作站上;2)由于移动成本较高,工序75只能分配到既定工位上;3)任务再分配过程中不增加总的工位个数,即不增加工人数量及相应人工成本。

表2 工序信息变动统计表
2 任务再分配的启发式算法
平滑指数(smoothness index,SI)是表征装配线工位负荷相对平滑性能的指标,定义如式(1)所示。平滑指数越小,装配线越平滑,系统生产效率也就越高[12]。因此,本文以最小化平滑指数为目标对任务进行再分配启发式算法设计以实现装配线的再平衡。

式中STk表示工位k的工作负荷,STmax表示所有工位的最大负荷。
定义问题任务集为T,任务数量为ntask,i、j为两个不同的工序任务,S为工位集,nposition为工位数量,S(k)表示集合S中第k个工位,AssTask(S(k),m)表示工位S(k)上的第m个任务,NumTask(S(k))表示工位S(k)上的数量。设固定工位任务集合为T1,固定工作站任务集合为T2。在调整过程中,若任务j在可以调整到任务i所在工位上并紧邻任务i,则称任务j属于任务i的可相邻工序集T(i)。
算法具体执行步骤如下:
步骤1:从1到nposition计算S(k)的结束时间,作为工位S(k)的装配时间,并对S(k)按时间长短进行排序,依据排序结果将对应k值依次存入数组Seq,令l=1,m=1;
步骤2:从任务集T中搜索工序AssTask(S(Seq(l)),m)的可相邻工序集T(AssTask(S(Seq(l)),m)),令T(AssTask(S(Seq(l)),m))=T(AssTask(S(Seq(l)),m)) -T1,若T(AssTask(S(Seq(l)),m))∩T2= ,执行步骤3,否则执行步骤5;
步骤3:将T(AssTask(S(Seq(l)),m))中任务按其所在工位装配时间长短排序,并依次搜索T(AssTask(S(Seq(l)),m))中工序是否可以调整到工位S(Seq(l))上,若可以调整并且能令SI降低,则进行调整,否则进行下一步;
步骤4:m=m+1,若m>NumTask(S(Seq(l))),且没有任务能分配到工位S(Seq(l))上,则执行步骤7,否则执行步骤2;
步骤5:将T(AssTask(S(Seq(l)),m))-T2中任务按其所在工位装配时间长短排序,并搜索T(AssTask(S(Seq(l)),m))-T2中工序是否可以分配到工位S(Seq(l))上,若可分配且使SI降低则进行分配,否则进行下一步;
步骤6:检测T(AssTask(S(Seq(l)),m))∩T2中任务所在的工作站,并枚举任务AssTask(S(Seq(l)),m)调整到该工作站的情况(包括开启新的工位),若SI降低,则进行调整,然后执行步骤4,否则进行下一步;
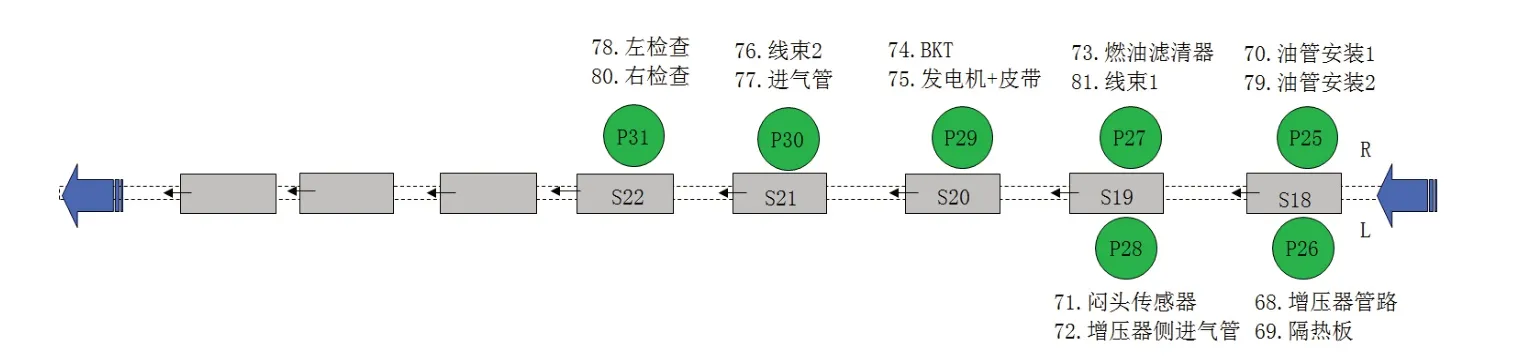
图2 调整后工作站{S18,S19,...,S22}的布局及任务分配图
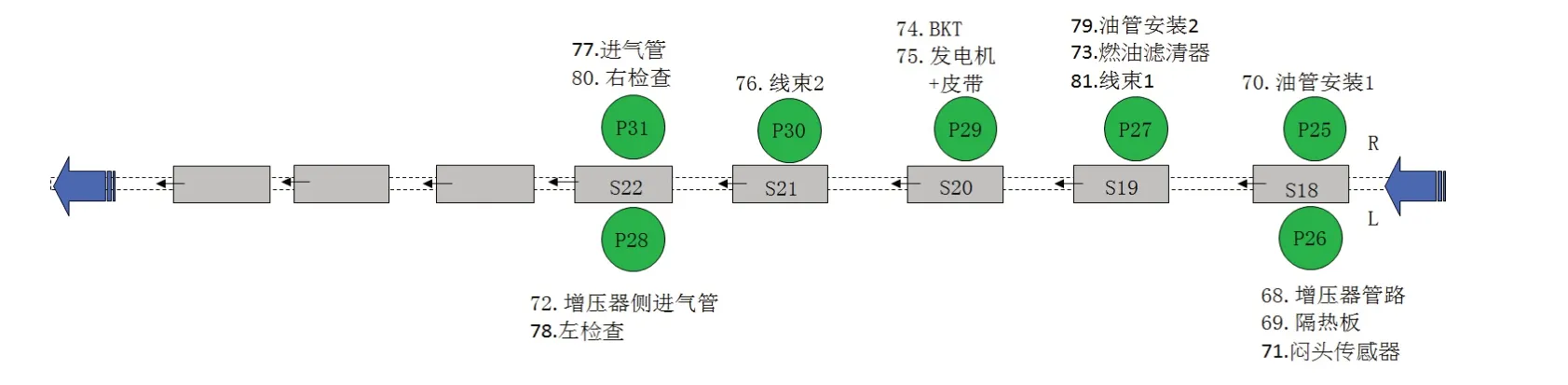
图3 再分配后工作站{S18,S19,...,S22}的布局及任务分配图

图4 发动机装配线的Plant Simulation仿真模型
步骤7:将工位S(Seq(l))从S集合中去除,并判断S集合中任务个数是否小于2,若满足,则结束,否则执行步骤1。
按照该算法对工作站{S18,S19,...,S22}进行任务再分配,再分配后的布局及分配情况如图3所示。
3 仿真分析
根据图1和表1所示,采用Plant Simulation建立该装配线的仿真模型,如图4所示,Station01、Station02、...、Station22分别表示工作站S1、S2、…、S22,P1、P2、…、P31分别表示对应工位,Station1Simulation、Station2Simulation、...、Station22Simulation用于对应工作站上不同工位任务执行过程的仿真控制。同理,可建立任务再分配后的仿真模型。
设定每天工作时间为8小时,无故障仿真运行100天,并分别采集工作站的工作时间、阻塞时间和饥饿时间进行对比,具体如图5所示,工作站的处理时间整体提升,阻塞时间和饥饿时间整体下降,装配线运行效率提升。日产量如表3所示,从63左右提升到了76台左右,产量提升效果十分明显,达到了产量的要求。

表3 日产量统计表
4 结束语
装配线中频繁出现的严重的阻塞和饥饿现象,对系统运行效率影响很大,针对该问题,本文首先对瓶颈工位周围部分装配工艺进行重新划分,然后以最小化平滑指数为目标,在充分考虑设备和空间约束下,制定启发式算法进行任务调整。最后仿真结果表明:再平衡后装配线上阻塞和饥饿现象减少,产量提升十分明显(日产量从63台左右提升到76台左右),该方法为装配线改进提供了一种可行方案。

图5 再平衡前后工作站运行状态对比图
[1] Emanuel FALKENAUER.Line Balancing in the Real World[A].Proceedings of the International Conference on Product Lifecycle Management[C],2005,5:360-370.
[2] S.M. RAMIREZ,L.M.T. TREVINO,M.G. CEDILLO, et al.Assembly Line Reconfiguration Under Disturbances: an Evolutionary Approach to Decision Making[A].Proceedings of the 15th International Conference on Computing[C],2006,6:24-32.
[3] Albert COROMINAS,Rafael PASTOR,Joan PLANS.Balancing Assembly Line with Skilled and Unskilled Workers[J].Omega,2008,36(6):1126-1132.
[4] Rita GAMBERINI,Andrea GRASSI,Bianca RIMINI.A New Multi-objective Heuristic Algorithm for Solving the Stochastic Assembly Line Re-balancing Problem[J].International Journal of Production Economics,2006,102(2):226-243.
[5] Gamberini R, Gebennini E, Grassi A, et al. A multiple singlepass heuristic algorithm solving the stochastic assembly line rebalancing problem[J]. International Journal of Production Research, 2009, 47(8):2141-2164.
[6] 杨才君,高杰,孙林岩.多目标混流装配线再平衡模型与算法[J].系统工程理论与实践,2013(8):1956-1964.
[7] Caijun YANG,Jie GAO,Linyan SUN.A Multi-objective Genetic Algorithm for Mixed-model Assembly Line Rebalancing[J].Computers and Industrial Engineering,2013,65(1):109-116.
[8] CaiJun YANG,Jie GAO.A Multi-objective Genetic-algorithm for Mixed-model Assembly Line Rebalancing Problems[A]. Proceedings of IEEE on Computers and Industrial Engineering[C],2010:1-6.
[9] F.S. OLIVEIRA,K. VITTORI,R.M.O. RUSSEL, et al.Mixed Assembly Line Rebalancing: a Binary Integer Approach Applied to Real World Problems in the Automotive Industry[J].International Journal of Automotive Technology,2012,13(6):933-940.
[10] Zhiyuan ZHU,Jie TAN,Wancheng NI, et al.A Multi-objective Dynamic Rebalancing Scheduling Algorithm for Mixed-model Assembly Line[A].Proceedings of IEEE on Information Science and Service Science and Data Mining[C],2012:586-591.
[11] J.J. BARTHOLDI.Balancing Two-sided Assembly Lines: a Case Study[J].International Journal of Production Research,1993,31(10):2447-2461.
[12] S. G. PONNAMBALAM,P. ARAVINDAN,G. MOGILEESWAR NAIDU.A Multi-objective Genetic Algorithm for Solving Assembly Line Balancing Problem[J].The International Journal of Advanced Manufacturing Technology,2000,16(5):341-352.

