大摆角摆臂式干涉仪非线性干涉信号光谱反演

谢运涛，张玉钧，程玉宝

(电子工程学院脉冲功率激光技术国家重点实验室，安徽合肥230037)

1 引言

傅里叶变换红外光谱仪是一种高灵敏度、高光谱分辨率的红外光谱探测设备，广泛应用于航天高光谱照相［1］、导弹尾焰分析［2］、有毒气体浓度检测［3－4］等领域。

干涉仪是傅里叶变换红外光谱仪的重要组成部分，其性能直接影响到光谱仪的光谱质量。摆臂式干涉仪与传统迈克尔逊干涉仪相比具有体积小、稳定性高、抗干扰能力强等优点［5］，其输出干涉图信噪比相对较高，得到了广泛应用。对于摆臂式干涉仪，在臂长相同的情况下，大摆角干涉仪与小摆角干涉仪相比具有更宽的光程差范围。但大摆角干涉仪的光程差随时间非线性变化，得到的是非线性变化的干涉信号，常规光谱变换方法(FFT)不适用非等间隔采样的信号，因此必须研究更加有效的光谱反演方法［6－7］。对于非线性干涉信号，先要将其转换为线性信号，即利用干涉仪的光程差变化信息对非线性干涉信号进行校正。目前常用的校正方法是光程差替换法［8－9］，但该算法存在复杂度高、时效性差的问题，对于实时性要求较高的场合并不适用。本文研究了一种基于非均匀快速傅里叶变换的非线性信号光谱反演方法，并将该方法应用于摆臂式干涉仪光谱反演，验证了该方法的有效性，同时将反演结果与传统反演方法进行了对比。

2 光程差非线性变化对光谱图质量的影响

摆臂式干涉仪机械结构如图1所示。

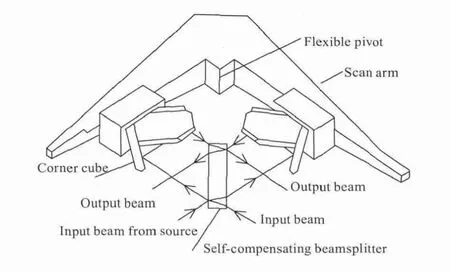
图1 叉骨干涉仪结构Fig.1 Constitution of the swing arm interferometer

摆臂式刚体末端固定了两个立体角镜，干涉仪围绕中心点来回扭摆，实现光程差的改变。结构上，摆臂式干涉仪充分利用光路折叠，在相同的运动范围内，其光程差是传统干涉仪的8倍，有利于实现干涉仪的小型化，其光程差与摆动角度的关系可用式(1)描述［5］:

式中，θ表示叉骨中心线偏离的角度;r表示摆臂长度;δ表示两光束的光程差。

从式(1)可以看出，摆臂式干涉仪光程差随角度呈正弦规律变化。当角度较小时，可近似认为光程差线性变化。当摆角较大时，则非线性效应不可忽略。文献［10］深入研究光程差非线性效应对光谱图影响，得到干涉仪摆动角度对光谱的影响曲线如图2所示。

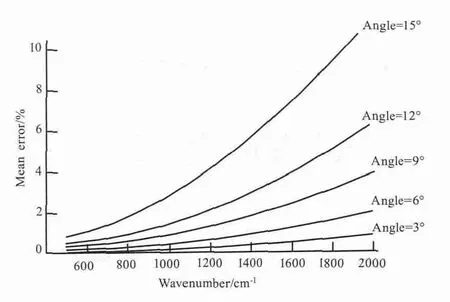
图2 光程差非线性对光谱的影响Fig.2 Effects of the non－linearity of the OPD on the spectrum

从图2可以看出，随着摆臂角度的增大，得到的光谱图平均误差越来越大。当干涉仪摆动角度大于6°时，光程差的非线性效应对光谱图的影响不可忽略。

为此，本文提出一种针对大摆角摆臂式干涉仪的非线性干涉信号光谱反演方法，与传统非线性干涉信号光谱反演方法相比，该方法具有算法复杂度低，反演速度快的特点。

3 非线性干涉信号快速光谱反演

非均匀快速傅里叶变换法将核函数、卷积算法、快速傅里叶变换算法三者相结合［11］，是一种针对非等间隔采样数据的快速时—频转换方法，适合于非线性信号的频谱分析。该方法与光程差替换法相比具有复杂度低、速度快的特点，其反演过程可分为以下几个步骤。

(1)构造非均匀采样信号f(x)。对于离散数据fj，将其构造成如式(2)所示的函数，xj为采样对应的光程差。

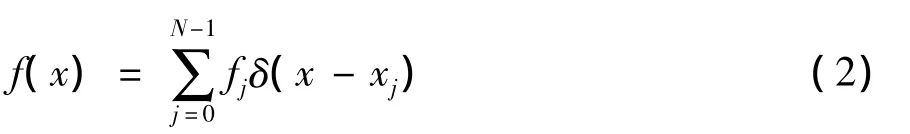
(2)选择合适的卷积核函数gτ(x)。常用的核函数有cosin核函数、B样条核函数、Kaiser－Bessel核函数以及高斯核函数。以高斯核函数为例，其表达式如下:

(3)对非均匀采样信号及核函数进行卷积运算，得到的fτ(x)可以看作是以2π为周期的周期函数:

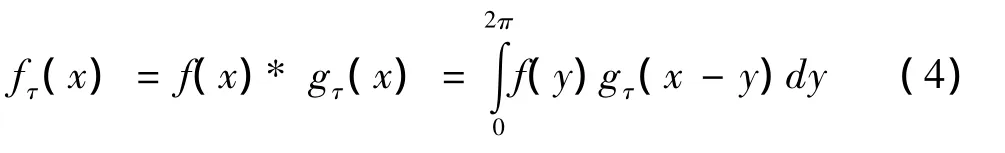
(4)对fτ(x)进行等间隔采样，这样就得到了均匀采样的干涉信号。采用快速傅里叶变换算法(FFT)计算fτ(x)的频率分布:

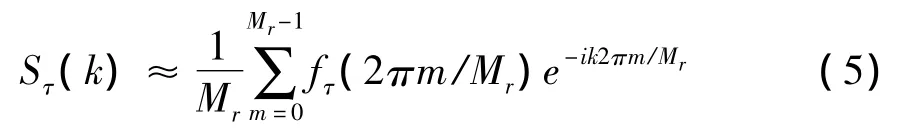
式中，Mr表示对fτ(x)过采样后的采样点数，一般取Mr=2N。

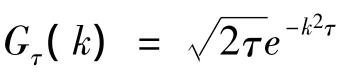
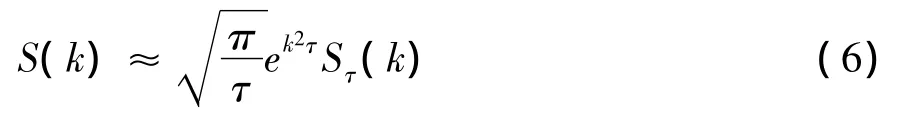
4 实验及结果分析

光程差替换法的本质是一种直接离散傅里叶变换法，它利用权重函数乘以离散采样数据以补偿光程差非线性对结果的影响［10－11］，也能够实现非等间隔采样干涉数据的光谱反演，其缺点在于算法复杂度高、运算速度慢。为比较上述两种方法的光谱反演效果，设置了以下实验进行验证。

实验系统如图3所示。实验中，红外辐射经光学系统准直后入射到干涉仪，经干涉仪调制的红外辐射穿透固定厚度的空气后入射到红外探测器。对得到的干涉信号由采集卡完成信号采集，最终由计算机完成数据的处理，处理时分别采用光程差替换法和NUFFT两种反演方法。实验系统将硅碳棒作为红外光源，DTGS探测器作为红外探测器件，干涉仪摆动角度可调，最大角度为15°，臂长为3 cm，可获得的最大光程差为6.2 cm，计算机采用i3－2120处理器，主频3.3 GHz，内存2 GB，操作系统为Windows xp。

图3 实验系统实物图Fig.3 Picture of the experimental system

分别设定干涉仪最大摆角为 3°、6°、9°及 12°，得到四幅干涉图。采用两种方法进行光谱反演，记录下每次光谱反演的时间，如表1所示。

表1 两种方法反演时间比较Tab.1 Comparison of operating time in different correcting methods

对于每一幅干涉图I，经反演得到三类光谱图，分别是未经校正的光谱图S1、采用光程差替换法校正得到的光谱图S2和采用NUFFT校正得到的光谱图S3。将摆动角度设定为12°时得到的I、S1、S2、S3分别对应图4、图5、图6、图7。

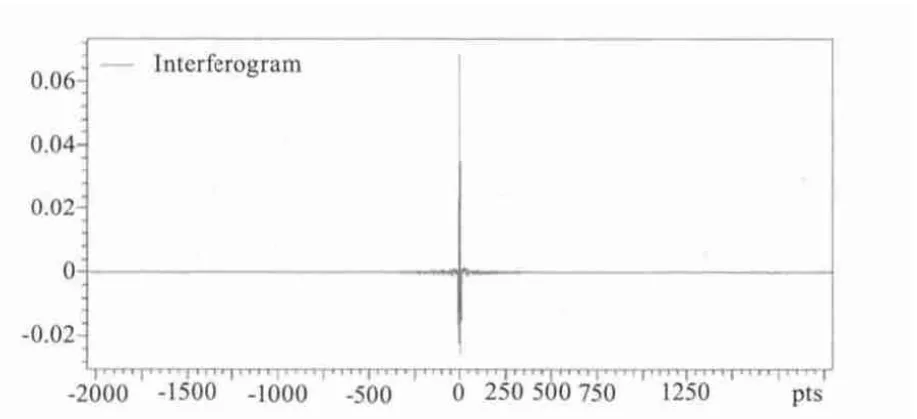
图4 干涉信号图Fig.4 The interferogram

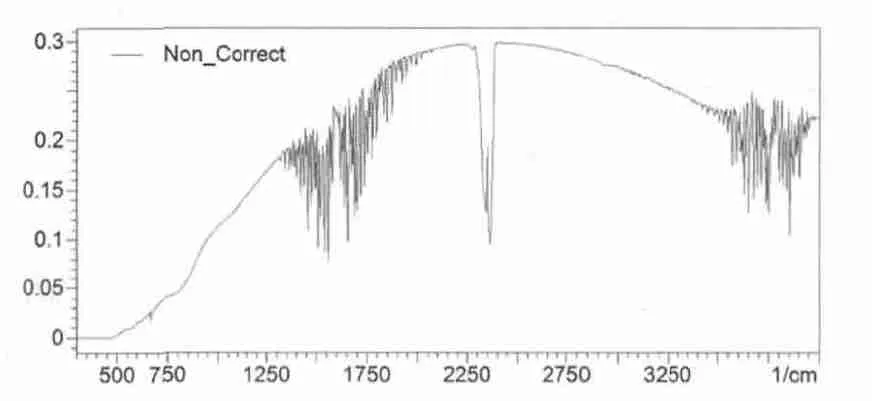
图5 未校正光谱图Fig.5 Non－corrected spectrum

从表1可以看出，非均匀快速傅里叶变换法与光程差替换法相比具有更快的运算速度，而且随着干涉仪摆动角度的增大，NUFFT算法相对于光程差替换法的优势越来越明显。

采用相对光谱误差函数［9］对上述三种光谱图之间的光谱误差进行分析，得到不同摆动角度(3°、6°、9°和12°)时三种光谱图的光谱误差如表2。

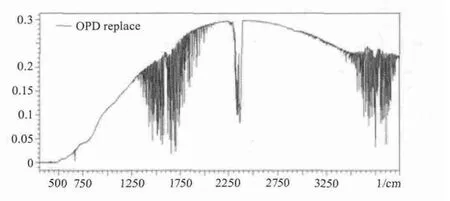
图6 光程差替换法反演光谱Fig.6 Corrected spectrum by OPD replace method

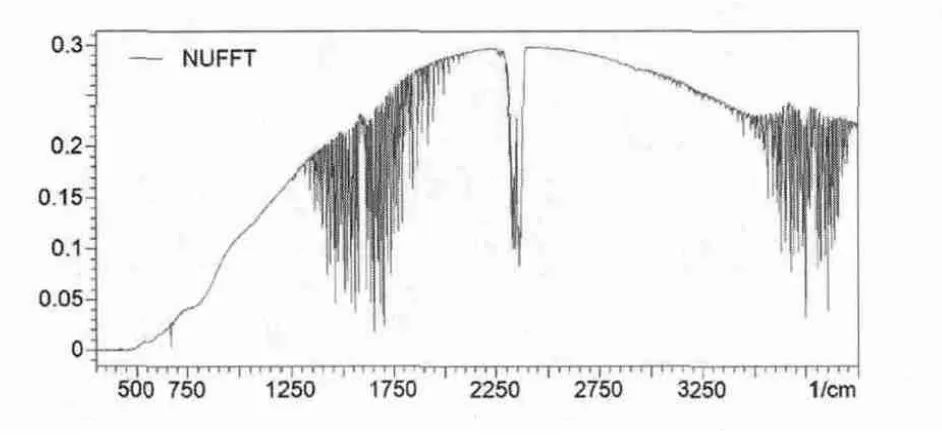
图7 NUFFT反演光谱Fig.7 Corrected spectrum by NUFFT method

从表2可以看出，随着角度的增大，校正后的光谱与未校正的光谱之间的差别越来越明显。两种校正方法得到的光谱图之间的差别较小，而且这种差别对角度的变化不敏感。

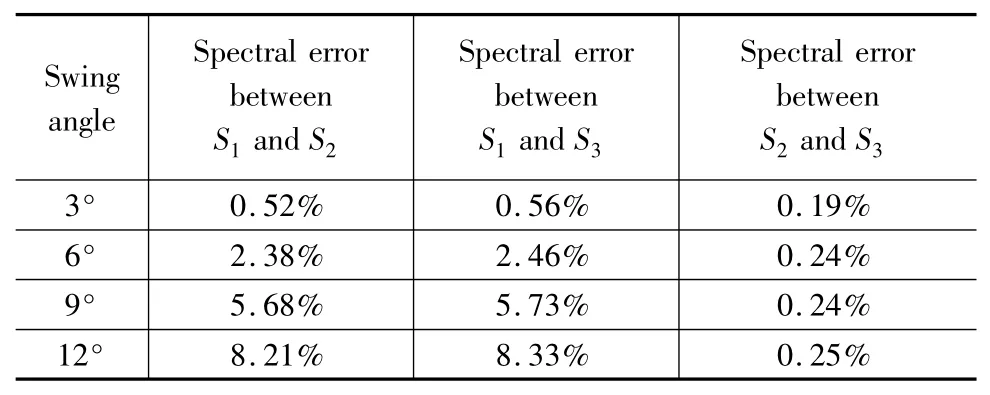
表2 光谱图误差Tab.1 Error between the recovered spectrums

5 结论

本文分析了摆臂角度对光谱图的影响，提出将NUFFT方法应用到大摆角摆臂式干涉仪非线性信号的光谱重建中，并详细介绍了该算法的工作机理。分别使用光程差替换法和NUFFT方法实现了干涉图数据的光谱反演，实验结果表明:NUFFT方法与传统方法相比光谱反演精度相近，但反演速度方面前者明显快于后者。因此NUFFT算法更适合于光谱实时性要求较高的应用场合。

［1］ Shimoda H.Overview of Japanese Earth observation programs［C］.Proc.SPIE，2010，7826:782602.

［2］ J Wang，Y Lou，Z Chen，et al.Study on infrared spectral radiance by remote Fourier transform infrared spectroscopy［J］.Spectroscopy Letters，1991，24(6):855－864.

［3］ Rochette L，Smith W L，Howard M，et al.ASSIST，atmospheric sounder spectrometer for infrared spectral technology:latest development and improvement in the atmospheric sounding technology ［C］.Proc.SPIE，2009:7457:745702.

［4］ Zhang Chunmin，Wang Wei，Xiang li Bin，et al.Interference image spectroscopy for upper atmospheric wind field measurement［J］.Acta Optica Sinica，2000，20(2):234－239.

［5］ Shi Yufeng.Research on the control technology for the interferometer subsystem in space－borne infrared spectrometer［D］.Huazhong:Huazhong University of Science and Technology，2012.(in Chinese)施宇锋.星载红外光谱仪干涉分系统的控制技术研究［D］.武汉:华中科技大学，2012.

［6］ Davis Summer P，Mark C Abrams，James W Brault.Fourier transform spectrometry［M］.New York:Academic Press，2001.

［7］ G AVanasse，H Sakai.Progress in optics VI［M］.Amsterdam North－Holland Publishing Company，1967.

［8］ ZHANG Mingjun，WANG Zhaoba，WANG Zhibin，et al.Fast spectral rebuild Garithmetic of PEM－FTS nonlinear phase interferogram data［J］.Chinese Journal of Lasers，2013，40(5):0515001.(in Chinese)张敏娟，王召巴，王志斌，等.PEM－FTS非线性干涉信号快速光谱反演算法［J］.中国激光，2013，40(5):0515001.

［9］ JING Juanjuan，ZHOU Jinsong，XIANG LIbin，et al.Comparison of correction methods for nonlinear optic path difference of reflecting rotating fourier transform spectrometer［J］.Spectroscopy and Spectral Analysis，2010，30(6):1678－1682.(in Chinese)景娟娟，周锦松，相里斌，等.反射转镜式干涉光谱仪光程差非线性修正方法比较［J］.光谱学与光谱分析，2010，30(6):1678－1682.

［10］ M T Surh.The effect of time jitter in sampling of an interferogram［J］.Applied optics，1996，5(5):880－881.

［11］ Dutt A，Rokhlin V.Fast Fourier transforms for non－equispaced data［J］.SIAM Journal on Scientific Computing，1993，14(6):1368－1393.