基于欠采样谱分析的激光拍频相位式测距方法

谢文锋,李孟麟,周维虎,李 锋,任建峰

(1.中国科学院光电研究院,北京100094;2.中国科学院大学,北京100049)



·激光应用技术·

基于欠采样谱分析的激光拍频相位式测距方法

谢文锋1,2,李孟麟1,周维虎1,李 锋1,任建峰1

(1.中国科学院光电研究院,北京100094;2.中国科学院大学,北京100049)

介绍了一种高精度相位式测距方法,载波通过双频氦氖激光器加偏振器产生1.08 GHz光强调制的拍频信号来实现,以克服半导体激光器的调制带宽限制,从而提高测距精度。为降低高速ADC实现难度,根据带通抽样定理,采用欠采样的方法采集波形数据,分析了其理论依据；然后通过全相位谱分析法对采样数据进行鉴相,并重点分析了鉴相数据的截取问题。搭建系统实验,在采样率为50 MSa/s时,157个欠采样数据就能实现0.1 mm左右的测距精度。实验表明,应用欠采样全相位谱分析法,以远低于测尺频率的采样率采样依然能实现高精度测距。

相位式测距；双频激光；拍频；欠采样；全相位谱分析鉴相法

1 引 言

测距精度和测量速率是相位式激光测距的重要性能指标,在机床生产控制、轨道在线检测、激光三维扫描仪、激光雷达等应用中,对在保证测量速率的前提下提高测距精度,提出了越来越高的要求。激光的调制频率称为测尺频率,在鉴相精度一定的情况下,提高测尺频率有利于提高测距精度。传统的相位式激光测距大都以半导体激光器作为光源,通过电流调制的方法调制出射的激光,由于半导体激光器的调制带宽限制,调制频率提高到几百兆时会有波形畸变、信号失真的问题,不利于测距精度的提高[1]。

双频氦氖激光器能够发出两束正交偏振且有一定光频差的激光,如果用一定的方式使两束激光的偏振方向相同,就能使两束激光发生拍频作用合成为光强正弦调制的激光,调制频率即为两束激光的光频差。这种方式能获得比半导体激光器更高的调制频率,理论上调制深度能达到100%,信噪比高,且调制频率稳定、波形失真小,是一种良好的高精度测量光源[2]。

为了实现通过提高测尺频率来提高测距精度,本文采用了频差达1.08 GHz的双频氦氖激光器作为光源,搭建拍频测距实验系统,利用欠采样方法以远低于载波频率的采样率采集波形数据,再用全相位谱分析法进行鉴相,计算获得测距值。

2 激光拍频测距系统

2.1 拍频合成调制波原理

设有传播方向重合、偏振方向相同的两束激光表示为：

s1=acos(2πf1t+φ1)

(1)

s2=acos(2πf2t+φ2)

(2)

其中，f1、f2分别为两束激光的光波频率;φ1、φ2分别为两束激光光波的初始相位。

两束激光叠加,得:

(3)

(4)

光电探测器接收的是激光的光强,光强与振幅的平方成正比,即:

(5)

其中，fB=f1-f2,可见合成后的光强变化是正弦调制的,调制频率为两束激光的频差。拍频合成过程如图1所示。

图1 激光拍频合成原理

双频激光器发出的是正交偏振光,实验中通过一块偏振片,使偏振片的偏振方向与两束正交偏振光偏振方向均呈45°角,如图2所示,获得两束偏振方向互相平行的偏振光,进而通过拍频获得光强为正弦调制的测量光源。

2.2 拍频测距实验系统

如图3所示,双频激光器产生两种光频率的激光,传播方向重合,偏振方向垂直,经偏振片后两束光偏振方向相同,产生拍频作用获得调制频率为fB的拍频光束,通过分光棱镜分成参考光路和测量光路,参考光和测量光由光电探测器接收,经放大后利用高速同步AD采样,将参考信号与测量信号数字化,得到的数据利用matlab实现的鉴相算法进行鉴相,获得距离信息。为便于实验本文采用移动测量光路的光电接收板的方法进行相对距离的测量。

实验装置如图4所示。实验中为提高信噪比,测量光路并未通过目标反射,而是分光之后直接在一定距离由光电探测器接收,然后利用示波器实现高速同步采样,采集的数据再用matlab进行数字鉴相实验,验证本测距方法所能达到的测距精度,为后续电路的设计提供参考。本文所用双频激光器频差约为1.08 GHz,即测尺频率约为1.08 GHz,参考信号和测量信号示波器显示如图5所示。

图4 实验装置

3 系统采样方法分析

3.1 欠采样原理及带通抽样定理

相位式测距的载波信号是带通信号,在一定条件下,以低于奈奎斯特采样率进行采样时,频谱不会发生混叠,采样后的频谱能无失真的还原信号,这种采样方式称为欠采样。欠采样可以降低对ADC的要求。

欠采样应遵循带通抽样定理。假设带通信号的最高频率为fH,最低频率为fL,带宽为B=fH-fL,根据文献[3],为保证频谱不混叠,应满足:

(6)

其中,m为正整数,且:

(7)

式(6)、(7)即是带通采样应满足的条件,m的意义如图6、图7所示。随着m值的不同,符合带通采样定理的采样率可以在一系列的采样率窗口中选择。当m=fL/B时:

fs≥2B

(8)

式(8)是fs的最低限,带宽越宽,fs的最低限越大,采样率的降低受到了前端滤波器的限制。对于相位式激光测距,真正有意义的是单一的信号频率,为保证频谱不混叠,要求噪声限制在带宽B以内。因此应用欠采样的方法采集波形对滤波器提出了更高的要求,采样率越低,要求采样前的带通滤波器带宽越窄[4-5]。

N点FFT变换结果是通过采样搬移后的频谱截取0～fs区段再N等分,所以频率分辨率为：

Δf=fs/N

(9)

设截取数据时间长度为T0=(1/fs)·N,由式(9)得：

Δf=1/T0

(10)

可见数据截取时间长度是频率分辨率的倒数,截取时间长度越长,频率分辨率越高。

图6 m为偶数时频谱搬移情况

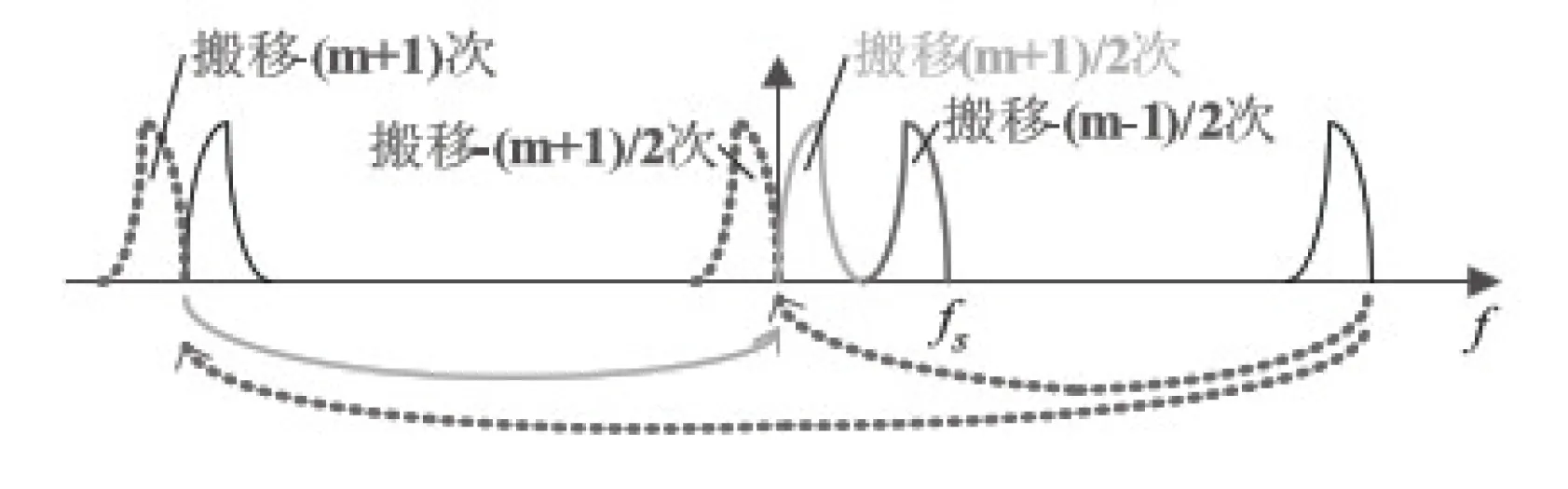
图7 m为奇数时频谱搬移情况

m为偶数时,如图6所示,设0～fs之间信号谱线位置为k(k取0～N-1),f为信号频率,由于频谱搬移后0～N/2为上边带,则由:

(11)

得:

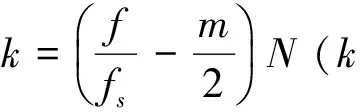
(12)

m为奇数时,如图7所示,N/2～N为上边带,由

(13)

得:

(14)

若分析相位时采用0～N/2的下边带,由:

(15)

得:

(16)

此时应注意k处谱线相位值是实际值的相反数。

当m=0时,由式(6)得:

fs≥2fH

(17)

带通抽样定理变为奈奎斯特抽样定理,此时由式(12)得:

(18)

可见奈奎斯特抽样定理是带通抽样定理在m=0时的特例,针对带通采样的分析也适用于奈奎斯特采样。

3.2 载波信号特性分析

双频激光器的频差即拍频合成后的测尺频率经示波器初步测量为1.08 GHz左右,为更精确地获得其中心频率,利用实验采集的数据进行FFT变换,在频域上分析信号的中心频率及频偏特性。由式(9)知提高频率分辨率应降低采样率及增大FFT点数,因此选取采样率为50 MSa/s,采集了N=106个点,则频率分辨率Δf=50 Hz,由式(6)得m=43,为奇数,FFT后选取N/2～N的上边带进行分析,如图8所示。

图8 FFT后的幅度谱

信号谱线k在645420～645560之间,由式(13)得f在1.082271～1.082278 GHz之间,因此载波中心频率精确到1.082275 GHz,带宽约7 kHz。

3.3 欠采样采样率窗口分析

载波f=1.082275 GHz,滤波器带宽B为5、10、15、20、25 MHz时,由式(6)、(7)得到如图9所示的采样率选择窗口,随着带宽增大,采样率窗口减小,呈金字塔型。为保证频谱不混叠,采样率必须在式(6)、(7)计算获得的与图9类似的采样率窗口中选择。例如选50 MSa/s时,必须保证带宽在10 MHz以内。对于ADC的实现难度而言,采样率越低越好,但是采样率的降低同时也降低了测量速率,而且还可能受到低速ADC输入带宽的限制,因此系统实现时采样率应结合实际的需求来选择。

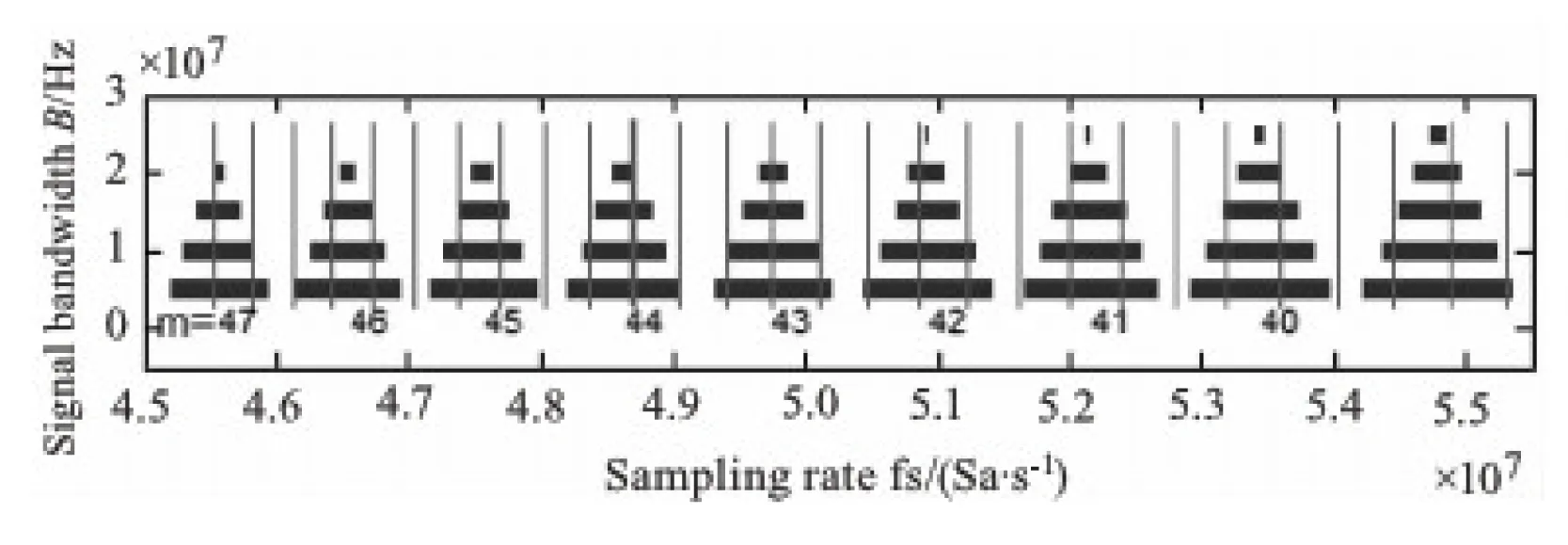
图9 采样率选择窗口及m值、带宽B的关系

4 系统鉴相分析

数字鉴相方法主要有数字相关法、数字同步解调法、频域数字鉴相法和全相位谱分析鉴相法。在信号的传播过程中,难免会混入光学的、电学的噪声,影响对信号的准确鉴相。全相位谱分析鉴相法具有鉴相准确度高,抗噪性能强的优点[6],更适于高精度鉴相场合。根据卷积窗的不同,全相位预处理过程又有矩形窗、汉宁窗和海明窗等类型,根据文献[7]的对比实验,无窗(矩形窗)全相位谱分析的鉴相性能最好。本文采用无窗全相位谱分析法进行鉴相。

4.1 全相位谱分析鉴相法

进行N点FFT变换,全相位预处理之前的数据点数为(2N-1)。全相位预处理过程如图10所示。

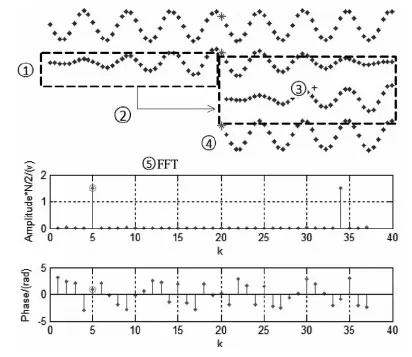
图10 全相位谱分析法基本过程(*为目标鉴相点)

此例中N=37,为便于分析采用了奈奎斯特采样。N点的矩形窗(即无窗)卷积后变为(2N-1)个点的三角窗,作为系数分别与(2N-1)个数据点相乘,形成中心权重大,两头权重小的数据(步骤1)；然后将鉴相目标点(即中心点)之前的(N-1)个点平移到中心点之后(步骤2)；分别与中心点之后的(N-1)个点对应相加(步骤3),与该中心点一起获得N个点的数据(步骤4)。然后对该全相位预处理之后的N个点进行FFT变换(步骤5),再进行频域的谱分析鉴相[7]。欠采样时的全相位谱分析过程与图10并无太大区别,只是随着m值的不同,信号谱线的位置会差异。

N点的FFT结果也是N个点,谱线中第1点频率为0,第(N+1)点为fs。通过式(12)、(14)、(16)或(18)取出k位置信号谱线的相位值,再求参考信号和测量信号的相位差,继而由式:

(19)

计算出测距值,其中Δφ为参考信号与测量信号相位差,c为光速,f为测尺频率。

4.2 鉴相数据的截取长度分析

式(12)、(14)、(16)、(18)中k与N的取值都为整数,但由于f=1.082275 GHz,fs与f没有一定的同步关系,其特殊性使k几乎不可能为整数,因此只能选择合适的N或者合适的fs使k尽量接近整数,从而使信号谱线能尽量落在FFT后能显示的谱线上,克服栅栏效应[8]。由于含m的项必然为整数,因此只要保证:

(20)

为整数即可,其中Ts为采样周期,T为信号周期,因此式(20)中kλ表示了所截取的信号周期数。使kλ为整数,在时域上是对信号进行整周期的截取。设dkλ=kλ-kz,其中kz为与kλ最接近的整数。如果截取的信号非整数个周期,即|dkλ|大到不可忽略的程度,则其在周期延拓时的衔接处有突变,产生高频分量,造成频谱泄露的现象[8],降低了鉴相精度。

在实际的硬件电路中,做FFT变换时N往往是2的整数幂,此时可以采取改变fs的方法,例如,当N为32时,图9的竖线表示符合整周期截取的一些采样率值,它们与带通抽样定理确定的采样率窗口交集的部分就可以选为硬件实现中的fs,但是这些fs包含的有效数字较多,应该再在其中选出容易取整的值,如粗竖线所示的48.709986 MSa/s,可以简略到48.71 MSa/s,此时32个点截取了711(710.9998)个信号周期。

具体实现中,可以由原信号频率通过一定方式得到fs,使得fs与f有一定的同步关系,或者由DDS细调产生fs,使得fs与f接近于一定的同步关系。还有一种方式是利用下混频电路,通过细调本振频率去抵消f中的小数项,使fs与f有一定的同步关系。

本文实验利用示波器进行采样,采样率和信号频率难以同步,只能通过改变N来获得数据的整周期截取。例如fs=50 MSa/s时,200以内符合偏差|dkλ|≤0.01的N只有79、127、158,对应的kλ为1710.0024、2748.9912、3420.0048,即分别截取了1710、2749、3420个信号周期,此时的N都不是2的整数幂。

另外,由式(10)知截取的时间长度是频率分辨率的倒数,截取时间长度越长,频率分辨率越高,越能克服频谱泄露,提高鉴相精度。

5 实验结果分析

参考信号接收位置不变,测量信号接收位置往远处移动了约20 mm,因为在实际测距时计算的是目标反射的光程,因此这里等效于移动了10 mm。利用200 MSa/s采样的数据,通过间隔抽取的方法获得100 MSa/s、50 MSa/s的数据,然后每列数据等间隔选取400个目标鉴相位置并保证这些位置在这三组数据中能一一对应,在这些鉴相位置处分别进行了N为79、158、237的全相位谱分析鉴相,获得测距值并对比分析如表1所示。

表1 400次测距均值和标准差分析

从表1中看出,当fs=200 MSa/s、N=79及237时,kλ偏离整数几乎达到了0.5,即截取的数据并非整数个周期,其测距标准差比其他近于整周期截取的数据大的多,可见,对数据的非整周期截取将会严重影响测距精度。

对比不同fs的测距结果,除上述非整数周期截取的特例外,相同N值时不同fs的测距标准差变化并不大,可见在尽量排除噪声干扰降低频谱混叠几率的条件下,选择不同的采样率基本不会影响测距精度。测距均值基本不受N值的影响,但与fs相关,这是抽取的样本有一定的差异性导致的。

N值增大时,测距标准差减小,这是因为增大了数据截取长度,提高频率分辨率,更能避免频谱泄漏,同时也减小了旁谱噪声的影响,提高了测距精度。

由表1可知,利用欠采样全相位谱分析法进行激光拍频相位式测距,157(N=79)个欠采样数据其测距精度就能达到0.1 mm 左右,而473(N=237)个欠采样数据其测距精度达到了约0.06 mm。由于测尺频率高达1.082275 GHz,故单频测尺长度只有138.6 mm。

6 结 论

本文实验表明,利用双频激光拍频的方法,可以获得比半导体激光器电流调制法产生更高的测尺频率,以提高测距精度。同时,利用欠采样全相位谱分析法可以以远低于测尺频率的采样率获得较高的测距精度,157个欠采样数据其测距精度就能达到0.1 mm 左右(测尺长度138.6 mm)。在尽量排除噪声干扰的条件下,欠采样时采样率的差异几乎不会影响测距精度。实验中测尺频率与采样频率不同步导致难以整周期截取的问题,在电路实现时,可通过细调采样频率或利用下混频细调本振频率来解决。

[1] JIANG Chenghao,YANG Jinhua,et al.High-precision phase-shift laser range finder system based on laser beat-frquency[J].Acta Photonica Sinica,2014,43(9):0912006.(in Chinese)

姜成昊,杨进华,等.基于激光拍频高准确度相位式测距方法[J].光子学报,2014,43(9):0912006.

[2] ZHANG Shulian,LI Yan.Dual frequency laser and related measurement science technology for 21st century[J].China Mechanical Engineering,2000,11(3):266-269.(in Chinese)

张书练,李岩.面向21世纪的双频激光及相关测量科学技术[J].中国机械工程,2000,11(3):266-269.

[3] FAN Changxin,CAO Lina.Communication principle[M].6th ed.Beijing:National Defense Industry Press,2006:478-480.(in Chinese)

樊昌信,曹丽娜.通信原理[M].6版.北京:国防工业出版社,2006:478-480.

[4] WANG Xinyao,ZHANG Keshu.Digital phase-shift measuring methods based on sub-sampling in laser range finder[J].Infrared and Laser Engineering,2013,42(5):1330-1337.(in Chinese)

王心遥,张珂殊.基于欠采样的激光测距数字鉴相方法[J].红外与激光工程,2013,42(5):1330-1337.

[5] SUN Maoheng,ZHAO Wen.Precision improvement of undersampling theory using phasic laser rangefinder[J].Infrared and Laser Engineering,2009,38(1):70-73.(in Chinese)

孙懋珩,赵雯.应用欠采样原理提高相位式激光测距精度[J].红外与激光工程,2009,38(1):70-73.

[6] GOU Ningyi,ZHANG Keshu.High speed digital phase-difference measuring methods simulation and implementation in phase-shift laser range finder[J].Infrared and Laser Engineering,2012,41(9):2358-2363.(in Chinese)

缑宁祎,张珂殊.高速相位式激光测距数字鉴相方法仿真与实现[J].红外与激光工程,2012,41(9):2358-2363.

[7] WANG Xuangang,GOU Ningyi,ZHANG Keshu.ApFFT phase discrimination in phase-shift laser range finder[J].Information and Electronic Engineering,2012,10(06):725-729.(in Chinese)

王选钢,缑宁祎,张珂殊.相位式激光测距全相位谱分析鉴相算法[J].信息与电子工程,2012,10(06):725-729.

[8] CHENG Peiqing. Digital signal processing tutorial[M].3rd ed.Beijing:Tsinghua University Press,2007:129-138.(in Chinese)

程佩青.数字信号处理教程[M].3版.北京:清华大学出版社,2007:129-138.

Laser beat-frequency phase-shift ranging based on undersampling spectrum analysis

XIE Wen-feng1,2,LI Meng-lin1,ZHOU Wei-hu1,LI Feng1,REN Jian-feng1

(1.Academy of Opto-electronics,Chinese Academy of Sciences,Beijing 100094,China;2.University of Chinese Academy of Sciences,Beijing 100049,China)

A high accuracy phase-shift ranging method is introduced.Carrier wave is realized by 1.08 GHz intensity modulation beat frequency signal produced by a dual frequency He-Ne laser and a polarizer,and it overcomes the modulation bandwidth limitation of the semiconductor laser for improving the accuracy of ranging.In order to reduce the difficulty of high speed ADC implement,undersampling method was used to collect waveform data according to the band-pass sampling theory and the theoretical basis was analyzed.The phase-shift of the sampled data was discriminated by all phase spectrum analysis method and the interception problem of phase discrimination data was strictly analyzed.In the system experiment,the accuracy of ranging could be about 0.1 mm when sampling rate was 50 MSa/s and the number of undersampling data was 157.Experiment results show that high accuracy ranging can be realized with the sampling rate far lower than measuring tape frequency when the undersampling all phase spectrum analysis method is used.Key words：phase-shift ranging;dual frequency laser;beat-frequency;undersampling;all phase spectrum analysis

�信号和测量信号波形Fig.5 Waveforms of

ignal and measurement signal

1001-5078(2015)10-1194-06

国家自然科学基金项目(No.61205161)资助。

谢文锋(1989-),男,硕士生,主要从事激光测量技术,信号处理方面的研究。E-mail:fjxskywf@qq.com

2015-02-09;

2015-03-06

TN249

A

10.3969/j.issn.1001-5078.2015.10.010