基于数字流域系统的漳卫河系洪水演进模型建立

邢 斌，朱晓春，李永庆

（海河水利委员会科技咨询中心，天津 300170）

洪水的运动规律复杂多变，威胁人们正常的生产、生活，带来严重的生命财产损失和安全隐患。利用现代计算机技术，洪水演进模型能够根据上游干支流的洪水过程及区间来水，模拟计算下游任意断面的洪峰流量、出现时间、最高水位及洪水过程，同时能够模拟水流在蓄滞洪区内的运动规律，为流域防洪规划、洪水预报、控制工程调度等提供科学的决策依据。

目前，洪水演进模拟方法主要有水文学法、历史洪灾调查法、一维或二维水力学法等。其中，二维水力学模拟方法能够分别从时间与空间角度模拟洪水演进过程，提供更为直观的洪水淹没范围变化，特别是一维、二维、零维耦合的水力学模型能在大流域尺度内更好地为防洪调度的决策提供服务。

随着水力学模型技术日趋成熟，建模平台可以使用丹麦的MIKE 系列、荷兰的De1ft3D 等商业化软件，也可以采用我国自主开发的如天津大学、河海大学、清华大学等高校研制的洪水演进模型。其中，河海大学王船海开发的数字流域系统应用开发软件，因其可视化的建模、需求方案的可定制、计算成果的在线查询分析、动态显示等功能，在太湖、长江、淮河等流域有很多成功应用案例，如太湖流域洪水预报系统、三峡水库动库容预报调度系统、江苏省里下河河网水动力模型系统等。笔者采用数字流域系统建立海河流域漳卫河系洪水演进模型，依据漳卫河系的现行调度规划模拟了漳卫河系发生50年一遇洪水的演进过程。

1 流域概况

漳卫河系是海河流域最南部的防洪骨干水系，流经山西、河南、河北、山东、天津四省一市，流域面积3.76 万km2，西以太岳山为界，南接黄河、徒骇马颊河，北界滏阳河，东达渤海。流域地形总的趋势西高东低，地面坡度山区丘陵区为10‰～0.5‰、平原为0.1‰～0.3‰。

漳卫河系由漳河、卫河、卫运河、漳卫新河、南运河组成。流域上游有漳河和卫河两大支流。漳、卫两河于徐万仓汇合后称卫运河，至四女寺枢纽，以下为漳卫新河和南运河。漳卫新河是漳卫河水系的入海尾闾河道。主要的蓄滞洪区有良相坡、长虹渠、白寺坡等。

2 模型建立及参数率定

漳卫河流域面积较大，河流众多，蓄滞洪区分布其中。根据流域实际情况，洪水演进模型需要建立一维、二维及零维模型。

2.1 模型原理

2.1.1 一维模拟

河道洪水波传播属不恒定流，其演变规律符合圣维南方程组，并采用偏微分方程的数值解法进行水流的数值模拟，公式如下：

式中：q 为旁侧入流（m3/s）；Q，A，B，Z 分别为河道断面流量（m3/s），过水面积（m2），河宽（m）和水位（m）；Vx为旁侧入流流速在水流方向上的分量，一般可以近似为0；K为流量模数，反映河道的实际过流能力；α为动量校正系数，是反映河道断面流速分布均匀性的系数；g 为重力加速度（m/s2）；t 为时间（s）；x 为距上一断面的距离（m）。

2.1.2 二维模拟

蓄滞洪区的水流采用二维浅水波方程来描述：

式中：Z为水位（m）；u，v分别为x与y方向上的流速（m/s）；U，V分别为x与y方向上的单宽流量（m3/s）为单宽流量的矢量，为它的模，；q为考虑降雨等因素的源项（m/s）；g 为重力加速度（m/s2）；c为谢才系数；f为柯氏力系数；wxt，wyt分别为风应力沿x和y方向的分量；t为时间（s）；h为水深（m）；ρ为空气密度（kg/m3）；x，y为自变量坐标。

对上述二维浅水波方程直接求解有一定的困难。因此，采用破开算子法将该方程分成如下两分步方程组，然后分别对其采用合适的方法进行求解。

第一分步为：

第二分步为：

对上面两分步方程组的数值求解，采用直角坐标系下非均匀矩形规则网格的控制体积法，具体方法如图1所示。

图1 二维差分网格示意

蓄滞洪区边界条件一般有堤，四周封闭，在大水情况下通过口门、漫堤、闸堰等与河道干流进行水量交换，其交换水量对行洪区讲是边界条件，对整个模型计算讲是内边界条件。

由单元I流进单元J的流量为QX=δX(ZI-ZJ)+βX，单元K流到单元J的流量为QY=δY(ZK-ZJ)+βY，对式（4）离散可得：

式中：A 为单元J 的面积（m2）；∑Qi表示包括降雨在内单位时间内流进单元J水量的代数和（m3/s）；Z为单元J的水位（m）；Δt为计算步长（s）。

2.1.3 零维模拟

计算软件对无地形资料的蓄洪区、湖泊等对象处理为零维区域，主要考虑水流在该单元区域内的调蓄作用，至于其中的运动规律则不考虑，仅仅考虑区域内的水位变化。水位的变化规律遵循水量平衡原理，流入区域的净水量等于区域内的蓄量增量，即进出蓄洪区内的水量等于其内的蓄量变化。其计算公式为：

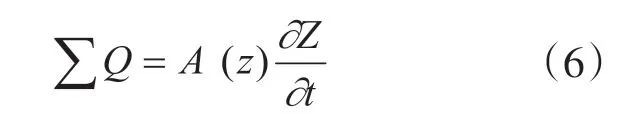
式中： )(zA为蓄洪区内水面面积（m2），一般为水位的某种函数关系；∑Q为蓄变量（m3/s）；Z为t时刻的水位（m）；t为时间（s）。

对式（6）离散后为：

式中：∑Q为蓄变量（m3/s）； )(zA为蓄洪区内水面面积（m2）；Z0为初始水位（m）；Z 为t 时刻的水位（m）；t为时间（s）。

2.1.4 模型耦合

流域洪水运动模拟由零维、一维、二维模拟所组成，各部分模拟必须耦合联立才能求解，而各部分模拟的耦合是通过“联系”来实现的。“联系”要素是指流域中控制水流运动的堰、闸及口门等，其过流流量一般以宽顶堰流量公式计算。

宽顶堰上的水流可分为自由出流、淹没出流两种流态，不同流态采用不同的计算公式。当出流为自由出流时，其计算公式为：

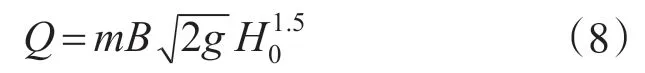
当出流为淹没出流时其计算公式为：

式中：B 为堰宽（m）；Z1为堰上水位（m）；Z2为堰下水位（m）；H0为堰上总水头（m），H0=Z1-Zd；hs为堰顶水深（m），hs=Z2-Zd；g为重力加速度（m/s2）；m为自由出流系数，一般取m=0.325～0.385；ϕm为淹没出流系数，一般取ϕm＝1.0～1.18；Zd为堰顶高程（m）。

对式（8）—（9）离散后，自由出流流量Q=δZ1Z1+βZ1，淹没出流流量Q=δZ2(Z1-Z2)。其中，δZ1，δZ2，1Zβ为与Z1，Z2有关的系数，一般常采用时段初水位来计算，有时为了提高计算精度，可采用迭代法计算。

2.2 模型建立

模型的建立主要包括地形及网格剖分、人工控制工程概化、控制条件设置、边界条件确立等。

2.2.1 模拟范围

本次涉及的模拟范围主要包括漳河、卫河出山口以下的河道及蓄滞洪区，即漳河（京广铁路桥下—徐万仓）、卫河（淇门—徐万仓）、卫运河（徐万仓—四女寺）、漳卫新河（四女寺—入海口）4 条主要河道，还包括淇河、汤河、安阳河3 条卫河的主要支流；大名泛区、良相坡、长虹渠（含柳围坡）、白寺坡、共渠西行洪区、小滩坡、任固坡7个蓄滞洪区。计算范围概化示意，如图2所示。

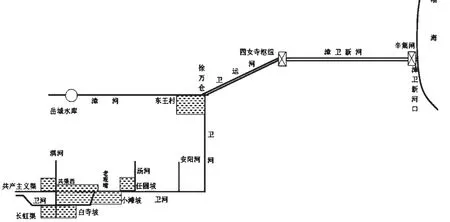
图2 洪水演进模型建模范围示意

2.2.2 数字地形与网格剖分

一维模型的地形数据是以1∶2 000 河道实测大断面资料为基础，将两堤坐标、起点距、高程导入断面编辑器，参与模型计算。断面编辑器中可以对河道进行主槽、滩地分界，设置糙率。河道断面编辑器界面，如图3所示。

图3 河道断面编辑器界面

良相坡、长虹渠等蓄滞洪区地形数据是以1∶10 000地形图提取的散点高程为基础，以蓄滞洪区围堤为固定边界，将x，y，z文件导入软件，生成不规则三角网，得到模拟区域的地形文件，结果如图4所示。

本次二维计算采用单元中心的有限体积法进行数值模拟，计算区域采用直角坐标系下非均匀矩形网格进行地形的剖分。网格间距根据模拟区域面积大小、地形变化情况、模拟精度等因素综合分析后设置，当关注某一区域的水文要素时可以设置网格加密，分为单独横向加密和单独纵向加密以及局部单元格加密。模型模拟区域网格剖分结果，如图5所示。

小滩坡和任固坡无近期地形资料，利用水位－蓄量关系建立零维模型，以水位节点的形式参与计算，忽略其内部流场。零维要素编辑器界面，如图6所示。

图4 蓄滞洪区（以大名泛区为例）地形高程渲染

图5 蓄滞洪区（以大名泛区为例）地形剖分

图6 零维要素编辑器界面

2.2.3 工程模拟

工程设施主要是指流域中控制水流运动的堰、水闸及蓄滞洪区分洪口门等。这些设施的过流满足水力学上的堰流公式，其原理与模型耦合一致。模型中将工程概化为“联系”。河道上相邻的断面之间、不同河道的断面之间、河道断面与二维网格之间、不同的二维网格之间均可根据水流方向建立“联系”，分别模拟河道拦河闸、穿堤涵洞、分洪（闸）口门等水利工程。模拟这些工程时，首先根据本身实际坐标找到在模型中的位置，然后将闸底板高程、闸孔宽度、闸孔高度输入模型，如果是宽顶堰型，则只需输入堰顶高程和宽度。为了提高计算稳定性，根据剖分网格尺寸大小考虑将较宽的口门分为若干“联系”进行模拟，如网格边长200 m、口门宽度700 m可用3个宽度为200 m、1个宽度为100 m的“联系”组合模拟。

2.2.4 控制条件设置

水闸、口门等工程的具体控制调度方法在模型中是以控制条件的形式实现的。本次计算的控制条件依据《漳卫河洪水调度方案》编写。临时破堤型口门，当水位或者流量达到调度条件时被扒开。由于破堤口门被炸开分洪时并不是瞬间达到最大宽度，模型中考虑了口门宽度发展速度控制，即模拟口门自扒开至最大口门宽度这个过程随时间变化的实际情况。

2.2.5 边界条件确立

模型中共有5个洪水入口，分别是漳河入流、良相坡入流、淇河入流、汤河入流和安阳河入流，其设计洪水流量过程作为模型的上边界条件；1 个洪水出口，即漳卫新河河口，其设计潮位过程作为模型的下边界条件。模型边界条件示意，如图7所示。

图7 模型边界条件示意

2.2.6 露滩问题处理

对于水流还没有流到的露滩区域，需进行特殊处理。目前，比较合理的方法是采用动边界方法确定出计算域中有水和无水区域的界限进行模拟，但是在程序编译处理过程中比较复杂困难。本模型作近似简化处理，通过“冻结法”和最小水深假设的方法把露滩问题处理为固定边界。

2.3 参数率定

计算模型的主要参数包括用于计算河道流量模数（K）的曼宁糙率系数（n）、计算分洪口门流量的堰流系数（m）。其中，分洪口门一般按照自由出流考虑，堰流系数一般取0.325～0.385，考虑到分洪口门没有控制闸门，计算中一般按低限考虑，可不设定。因此，模型计算时需要设置的主要参数是糙率。

天然河道的糙率一般与断面形状、河床特性等因素有关，变化范围较大。由于没有完整的实测资料来率定模型糙率参数，目前采用漳卫河系防洪规划成果中的设计糙率。模型糙率取值，见表1。

表1 模型糙率（n）取值

3 模拟计算

运行模型之前需要给定初始条件，对于流域模型而言，上游至下游主要洪水流路必须通畅，有条件控制的分洪口门及蓄滞洪区不参加初始条件计算。给定一个高于最高地面高程的水位值进行初始条件计算，当整个模型的水位变幅为0 即初始条件计算达到恒定时开始正式计算。

选取50年一遇设计洪水过程，利用之前制作的地形及模型参数，进行漳卫河系洪水演进模拟，不仅可以获得蓄滞洪区洪水的淹没要素，还可以输出河道水面线、控制站水位（流量）过程、蓄滞洪区控制点水位、蓄滞洪区最大入流、出流等。主要计算结果，见表2。

表2 50年一遇洪水模拟主要成果

洪水演进过程支持实时查询，即在地图上点击任意位置，就可获得该时刻该位置的水位、水深、流速、水量、地形高程等信息。以洪水入流后160 h为例，蓄滞洪区对应的淹没范围、河道水面线、流量过程、水位过程，如图8—10所示。

图8 长虹渠淹没范围

图9 卫运河水面线

图10 四女寺枢纽流量、水位过程（当发生50年一遇设计洪水时）

经过对比，本次研究洪水演进的成果与防洪规划成果有所不同，主要不同点见表3—4。

表3 河道计算成果对比水位：m；流量：m3/s

表4 蓄滞洪区计算成果对比水位：m；流量：m3/s

本次研究洪水演进成果与防洪规划成果之所以有所不同，是由于两次洪水演进采用的口门规模、运用规则不同。本次研究按照现行调度方案编写控制条件。如，规划中王湾口门宽度采用800 m、淇门160 m、圈里口门200 m，本次研究分别采用370、380、140 m，底高也不尽相同（见表5）；本次研究长虹渠仅通过淇门入流，而规划先运用宋村进行分洪；本次研究白寺坡王湾入流大于规划，是由于共渠西上部李桥水位高于63.471 m 时即通过邢固扒口分洪入白寺坡，白寺坡最大入流为邢固、王湾合计最大，而规划中邢固口门未启用。总体上讲，本次研究洪水演进的结果较为合理，与规划报告的趋势保持一致。

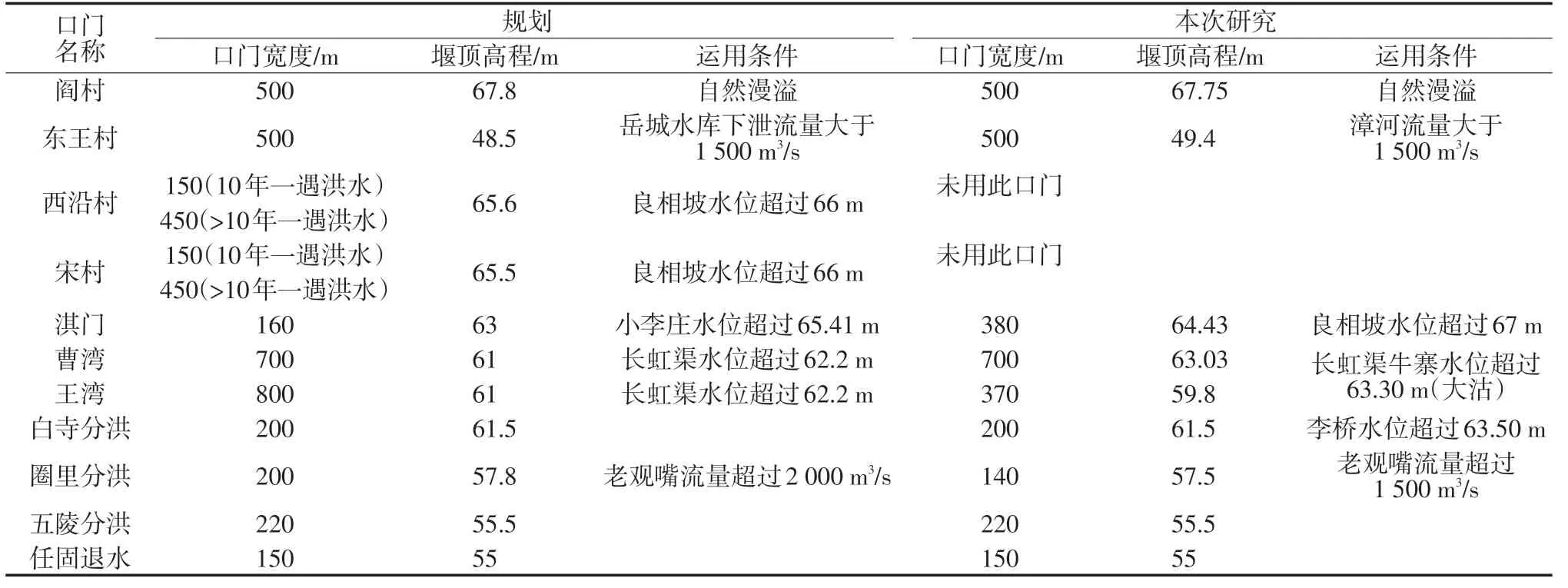
表5 规划与本次研究采用口门规模及控制条件对比

4 结论

笔者以漳卫河系洪水演进为例研究了数字流域系统模拟一维、二维、零维水力学的建模过程，得到以下主要结论。

（1）数字流域系统中的水动力学模块能够较好地应用于大型流域河网一维、蓄滞洪区二维及零维洪水演进数值模拟。本次研究以漳卫河山区以下发生50年一遇洪水时按照《漳卫河洪水调度方案》进行调度为模拟对象，与以往成果进行对比验证，结果显示模型的模拟精度满足工作需要，可用于平原河网地区、大型流域的洪水演进分析。

（2）二维模型采用隐格式有限体积法计算，在满足模型稳定性和精度要求的条件下计算步长可达600 s以上，计算效率较高。较快的计算速度使模型能够应用于洪水预报、调度方案调整、大型流域防洪规划等领域。

（3）由于海河流域缺乏完整的实测洪水资料，本次计算仅使用以往规划成果所采用的模型参数进行模型调试，再与规划成果进行对比，分析各项条件的异同，判断计算结果及其趋势是否合理，因此对模型验证结果的可靠性支撑略显欠缺。未来，随着流域洪水记录的积累，可对模型进行更为全面的验证，以进一步提高模拟精度。

[1]田景环，李芳芳.河道洪水演进浅析及一维数学模型的建立[J].中国水运，2007，（8）：94-95.

[2]魏凯，梁忠民，王军.基于MIKE21 的濛洼蓄滞洪区洪水演算模拟[J].南水北调与水利科技，2013，（6）：16-19.

[3]王船海，李光炽.行蓄洪区型流域洪水模拟[J].成都科技大学学报，1995，（2）：6-14.

[4]周潮洪，杜津媛，常守权.蓄滞洪区二维洪水演进系统的建立[J].海河水利，2002，（6）：33-34.

[5]海河水利委员会.漳卫河系防洪规划[R].天津：海河水利委员会，2008.