基于一维圣维南方程输水河道非恒定流模拟与沿线口门水位变化规律研究

陆莘阳，周 杨，陆红芳，陈运杰

（1.江苏省工程勘测研究院有限责任公司，江苏 扬州 225002；2.江苏省水利勘测设计研究院有限公司，江苏 扬州 225009；3.江苏省太湖地区水利工程管理处，江苏 苏州 215128）

1 概述

梯级泵站级间输水河道通常采用天然河道输水，可以简化为一维明渠非恒定流。如果在给定初始条件及各边界条件情况下，根据不同用水户的用水位置、用水流量，求出下一梯级泵站的站下水位，对泵站优化运行工况调节提供技术支持。同时，对农业、工业、生活、生态、船闸5大类型用水户确定合适的取用水方案具有实际指导意义[1]。

2 河网水动力模型原理

2.1 基本方程

河网模型以Saint-Venant方程组为基本方程描述河道一维非恒定流[2-3]。该方程组的基本形式是：

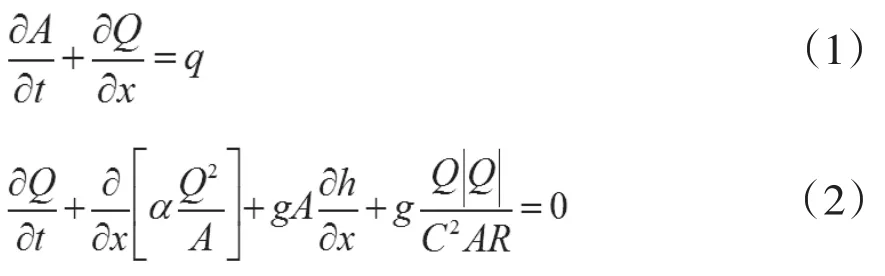
式中：x为距河道某固定断面沿水流方向的距离；t为时间；A为过水断面面积；Q为对应断面流量；h为水位；q为单位河长长度的旁侧入流（或流出）流量；R为水力（或阻力）半径；C为谢才系数，，n为河道糙率；α为动量校正系数；g为重力加速度。

式（1）为连续性方程，是质量守恒定律在流体力学中的具体表述形式，显示河道中水量平衡。该方程根据水量平衡原则推导而来，表述了由于流量的沿程变化而引起的过水断面面积随时间的变化。当水位上涨时，由于上游断面流量大于下游断面流量，即流量沿程递减，＜0，过水断面面积随时间递增，＞0，水位不断上升，河槽蓄量增加；反之，当落水时，流量沿程递增，＞0，过水断面面积随时间递减，＜0，水位下降，河槽蓄量减少。

2.2 定解条件

（1）初始条件

初始条件主要包括河床高程、初始水位。河床高程即为河床初始地形，可由近期实测河道断面数据获得；初始水位通常为给定常数，可设置为河道正常蓄水位[4-5]。

（2）边界条件

一维河网模型中有3种常见类型的边界条件：水位边界 h=h（t）、流量边界 Q=Q（t）及水位流量关系边界Q=Q（h）。上述3种边界依循水流连续性方程可统一转换为水位与时间的函数。由基本方程求解过程知，当上、下游节点水位Hus和Hds已知，即可求解一维圣维南方程组[6-7]。

一般而言，河道上边界采用进口断面流量过程，下边界为出口断面水位过程。

3 梯级泵站级间输水河道非恒定流模拟

3.1 河道基本资料

南水北调梯级泵站级间输水河道长度不等，现取有代表性的某级间输水河道，全长49.6 km，现状河道底宽60～70 m，底高程在11.5～14.0 m左右，边坡1:3，青坎15.0 m左右。

3.2 输水河道沿线用水户用水情况

通过对沿线用水户的分类统计发现，不同梯级泵站级间的用水口门（取水口）从0到22个不等。为方便研究，现将该级间输水河道上的用水口门数量简化为1～3个。

3.3 初始条件及边界条件的设定

（1）初始条件：给定河道上级泵站站上水位

19.55 m。

（2）边界条件：下级泵站供水流量为Q=230 m3/s。

3.4 方案比较

（1）单个口门位置不变，口门取水流量可变方案1：单个口门位置设在里程25 km处，口门流量10%Q；

方案2：单个口门位置设在里程25 km处，口门流量20%Q；

方案3：单个口门位置设在里程25 km处，口门流量30%Q。

结论：单个口门位置一定，当口门取水流量越大时，下级泵站站下水位越低（详见图1）。方案1的水位最高，方案3的水位最低，差值为6.5 cm。

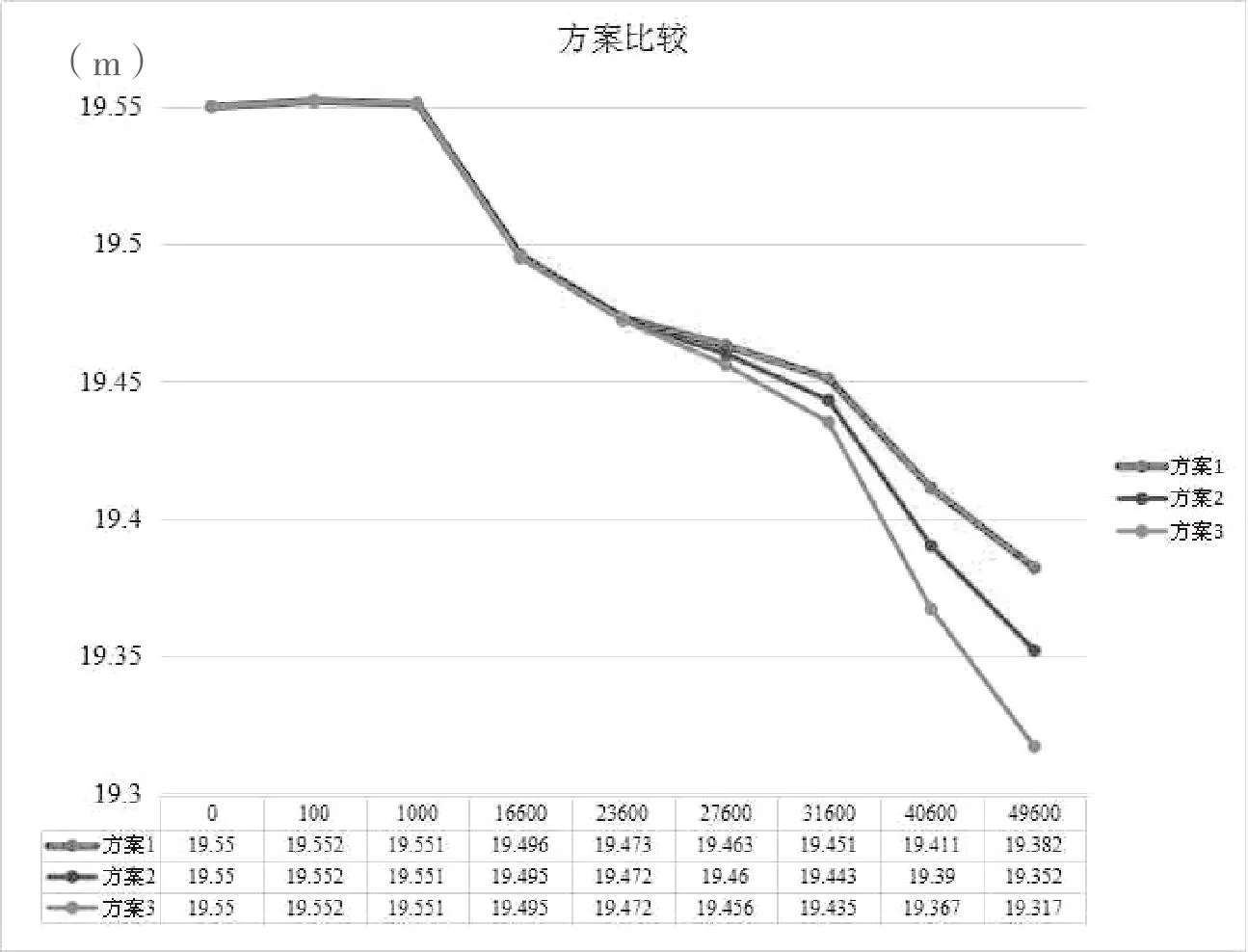
图1 单个口门位置不变时水位随用水量变化的关系曲线

（2）单个口门位置可变，口门取水流量不变

方案1：单个口门位置设在里程16.6 km处，口门流量30%Q；

方案2：单个口门位置设在里程25.0 km处，口门流量30%Q；

方案3：单个口门位置设在里程38.6 km处，口门流量30%Q。

结论：单个口门取水流量一定，当口门位置距离下级泵站越近时，下级泵站站下水位越低（详见图2）。方案1的水位最高，方案3的水位最低，差值为2.7 cm。

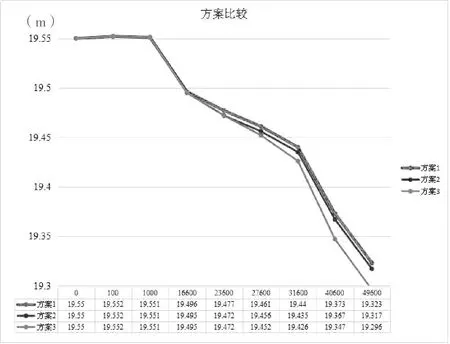
图2 用水量不变时水位随单个口门位置变化的关系曲线

（3）多个口门位置可变，口门取水总量不变

方案1：2个口门，口门位置分别设在里程16.6 km和里程25.0 km处，口门取水总量2×15%Q；

方案2：2个口门，口门位置分别设在里程16.6 km和里程38.6 km处，口门取水总量2×15%Q；

方案3：2个口门，口门位置分别设在里程25.0 km和里程38.6 km处，口门取水总量2×15%Q；

方案4：3个口门，口门位置分别设在里程16.6 km、里程25.0 km和里程38.6 km处，口门取水总量3×10%Q。

结论：多个口门取水总量一定，当口门位置距离下级泵站越近时，下级泵站站下水位越低（详见图3）。方案1的水位最高，方案3的水位最低，差值为2.7 cm。

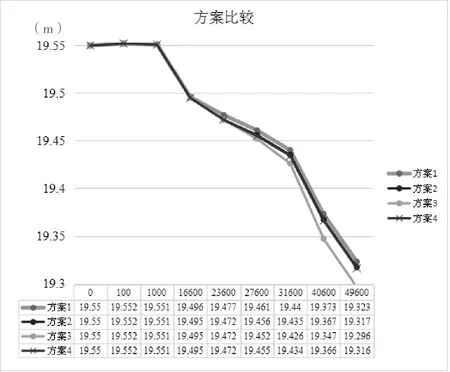
图3 用水量不变时水位随多个口门位置变化的关系曲线

4 结语

本文运用圣维南方程建立非恒定流模型，在口门位置不变、口门取水流量可变、口门位置可变、口门取水流量不变等多种工况下进行方案比较，不同的取水流量对下级泵站的站下水位影响较大，不同的口门位置对下级泵站的站下水位影响较小。因此，对用水户取水位置的准确性要求可以适当降低，即在输水河道长度足够长（＞20 km）时，在沿线用水量小于下级泵站供水流量30%的条件下，用水户的取水口门位置对水位的影响可以忽略不计，在优化调度模型开发中水位约束条件设定时，可以假定沿线用水户的取水口门集中为沿线的任意某一点。