船舶翼帆回转速度的非线性补偿控制

赵志强，闫亚胜，黄连忠，马冉祺，冯宝辉

(大连海事大学轮机工程学院，辽宁大连116026)

风力作为帆船的驱动力，在帆船自产生到发展过程中一直扮演着重要的角色。国内外对风帆助航技术的实用化和新型风帆的探索研究取得了长足的进步，如“新爱德丸”号的圆弧形硬质帆、Alcyone号的涡轮帆、“白鲸天帆”等，而与新帆型匹配的驱动机构要完成精确、稳定和安全的转帆功能，其设计和研究具有十分重要的意义［1-4］，如“新爱德丸”号硬质帆采用计算机控制，通过桅杆中的电磁阀精确调整帆角到最佳状态，从而辅助推动船舶［5］。

为实现控制其精确回转到最佳帆向角从而给船舶提供最佳辅助推力，设计并搭建翼帆回转液压实验台进行实验研究［2-3，6］。在实验中翼帆回转的起动加速、制动减速过程具有严重的非线性，造成难以精确控制、转帆精度不高等问题。因此，将对液压实验台驱动翼帆回转的阀控型开式液压系统建模分析，采用对比例调速阀进行非线性补偿控制的实验研究方法，使翼帆回转升、降速过程转速均趋于线性，有利于实现精确控制转帆机构。

1 翼帆回转实验台结构及工作原理

翼帆(风洞试验襟翼帆模型如图1)回转是全方位精确旋转，实验台采用低速大扭矩马达－减速齿轮－加载器(模拟翼帆受力)的结构［7］，如实物图2所示，其结构原理如图3所示。

图1 襟翼帆模型Fig.1 Wing-sail model

图2 翼帆回转液压实验台Fig.2 Wing-sail slewing hydraulic experimental table

图3 翼帆回转实验台原理图Fig.3 Wing-sail slewing table schematic diagram

工作原理为:阀控开式液压系统中定量泵为动力源，定量马达为执行元件，换向阀控制翼帆回转平台的左右回转;通过对比例调速阀施加一定的控制信号，调节系统液压油流量改变翼帆回转转速;翼帆所受的回转力矩由加载器模拟施加。

2 调速阀非线性补偿控制

2.1 补偿算法分析

首先对液压马达转速和调速阀电流的关系进行数学分析，液压马达的转速ω和转角θ为

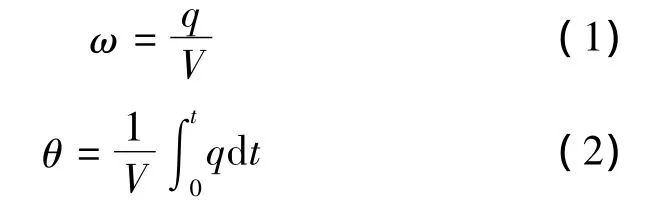
式中:q为马达液压油流量，V为马达单位转角排量。

流量控制阀是在一定的工作压差Δp下，通过阀口(节流口)通流面积A(x)的改变来实现对流量q的控制，遵照阀口流量公式:

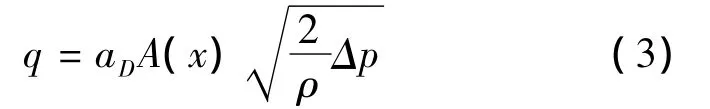
式中:aD为流量系数，可以近似为常数;A(x)为通流面积;ρ为油液密度。

作为压力补偿器的定差溢流阀，保持节流阀口的工作压差近似为一定值，使三通比例流量阀的输出流量q仅与通流面积A(x)有关:

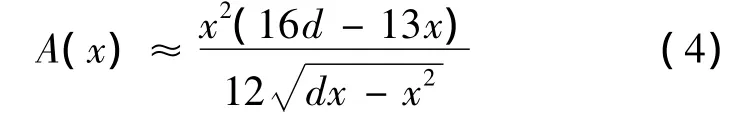
式中:x为阀芯位移，d为节流孔直径。

由比例电磁铁直接驱动阀芯时，如果忽略电磁铁和阀芯运动时所受的摩擦阻力及液压卡紧力，则其稳态平衡方程如下:

式中:KI、Kx为电磁铁的电流力增益和位移力增益，I、Ia为控制电流及起始电流，Krx为复位弹簧刚度，x0为预压缩量，Ff为稳态液动力。

通常情况下，Kx≪Krx，因此式(5)可改写为

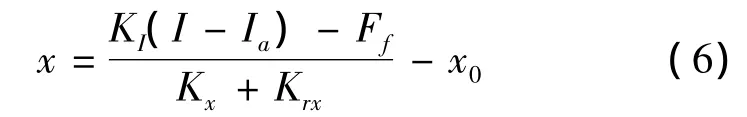
若不计液动力Ff，则阀芯位移x与输入控制电流成正比。

由以上分析及数学计算［8］，比例调速阀的磁滞现象、阀口流通面积等非线性因素均可以导致转速非线性的产生，通过上述分析最终可以归纳为转速ω与控制电流I具有一定的非线性函数关系(如图4)。

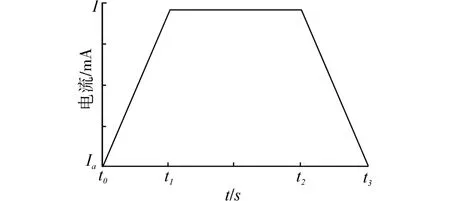
图4 控制信号形式Fig.4 Control signal on speed regulating valve

实验设计采用线性控制信号起动和制动的方式［9］，对翼帆的起动、制动转速和对应的调速阀电流进行多次测量，得到如图5所示的转速与调速阀电流关系曲线。

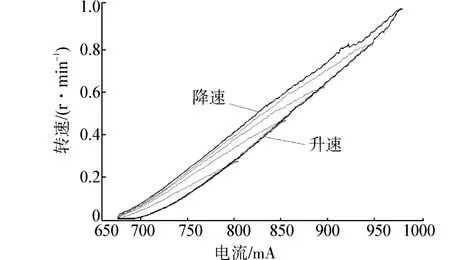
图5 转速－电流关系曲线Fig.5 Slewing speed against current curves

从图中5条不同折返曲线中可以看出，升速曲线明显呈非线性增长;各降速曲线基本呈线性状态，然而同一控制电流对应的转速均高于升速工况。实验表明，如果输入电流是从最小值开始，直至升速结束，那么不同折返转速的升速曲线合而为一且唯一确定，其数学模型可以表示为

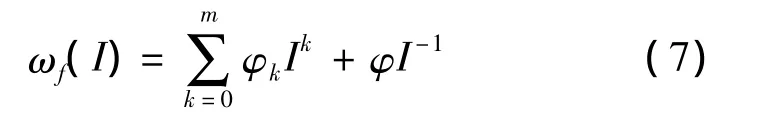
实验也表明，如果降速过程是从某一折返点开始，则其降速曲线也是唯一确定的，其数学模型可以表示为

式中:φk、γk、φ、γ为各项系数，由实验确定;m为阶数［10-11］。

通过实验得到各个转速工况下的升速、降速曲线数学模型，对系统采用开环控制，利用逆函数方法对其进行线性化补偿，如图6所示，设目标转速为R(I)，实际输出为R'(I)，ω(I)为转速模型函数，ω－1(I)为其逆函数，则补偿电流可以表示为

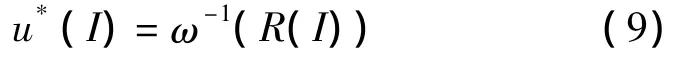
系统实际输出

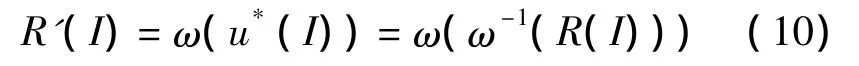
图6 转速－电流关系曲线Fig.6 Slewing speed against current curves

根据转速的期望输出R(I)反求系统输入u*(I)，使转速在该补偿电流作用下的实际输出R'(I)尽量接近期望输出R(I)［12］。

2.2 调速阀非线性补偿控制实验

实验液压控制系统总框架图如图7所示，上位机(PC机)将程序下载到下位机控制器并向控制器发出启动指令;下位机控制器将输出控制电流信号传输给调速器电磁阀，调节调速阀的阀芯位移，改变流量，进而改变马达转速;编码器将马达输出端角度编码值传回控制器，经过运算得到角速度值，在上位机程序中显示并存储。

图7 实验控制框架图Fig.7 Frame diagram of control experiment

实验中对翼帆最高回转速度为2、4、6(°)·s－13种工况进行升速、降速的补偿控制，得到3种速度在不同时域内(3.5 s和20 s)的升速、降速曲线如图8～10所示。

运用MATLAB中向量相关度corrcoef函数，求得各转速在起动、制动时间为20 s的补偿前后转速曲线与直线y=x(起动)或y=－x(制动)的线性相关度结果如表1所示，从各个图中及表1的结果中可以得出如下结论:

1)经过非线性补偿控制的升速曲线，不论最高转速是多大，不论升速/降速用时多长，都趋近于直线增长，线性相关度(基本大于0.998 0)均高于未补偿的升速曲线，完全优于未补偿的升速过程;

2)降速过程补偿前后转速曲线的线性度相差无几，补偿后略高;但原转速下降缓慢，最终在调速阀关闭时陡降;补偿后降速曲线斜率绝对值变大，速度下降更快，改善了制动结束时速度陡降。

图8 2(°)·s－1补偿前后起动和制动过程转速对比Fig.8 2(°)·s－1starting and braking process slewing speed comparison before and after compensation

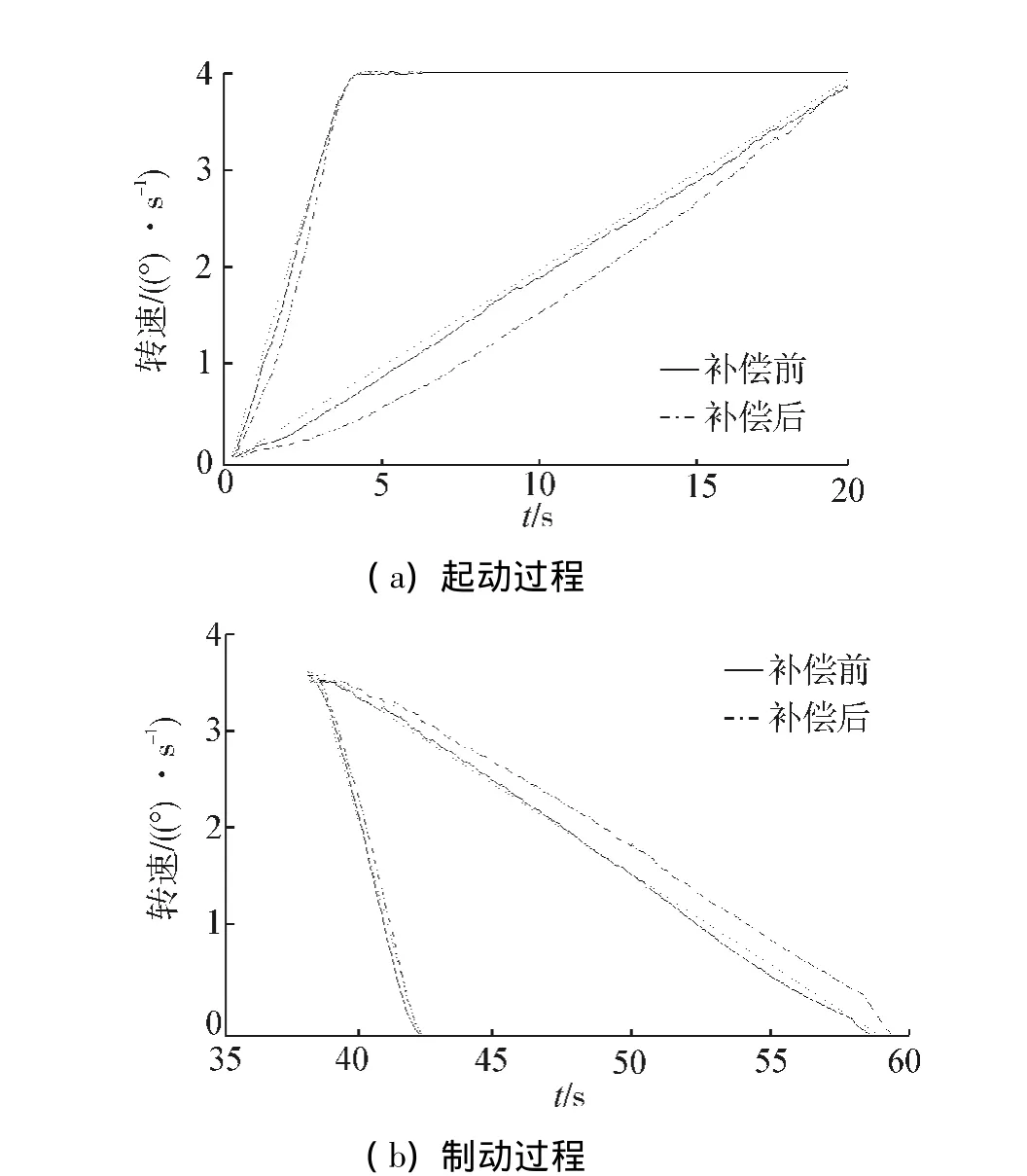
图9 4(°)·s－1补偿前后起动和制动过程转速对比Fig.9 4(°)·s－1starting and braking process slewing speed comparison before and after compensation

图10 6(°)·s－1补偿前后起动和制动过程转速对比Fig.10 6(°)·s－1starting and braking process slewing speed comparison before and after compensation

表1 时域20 s补偿前后转速直线相关度Table 1 20 s time-domain slewing speed linear correlation before and after compensation

此外，对调速阀电流信号进行补偿后，提高了转帆精度，补偿前后转帆角度对比如表2所示。从表中数据可以看出，未补偿的控制过程，转帆误差在－2.93～－0.56°，大部分工况的误差都已经高出1°;经过补偿控制的转帆误差，介于－0.99°和－0.26°之间，大大提高了转帆精度。

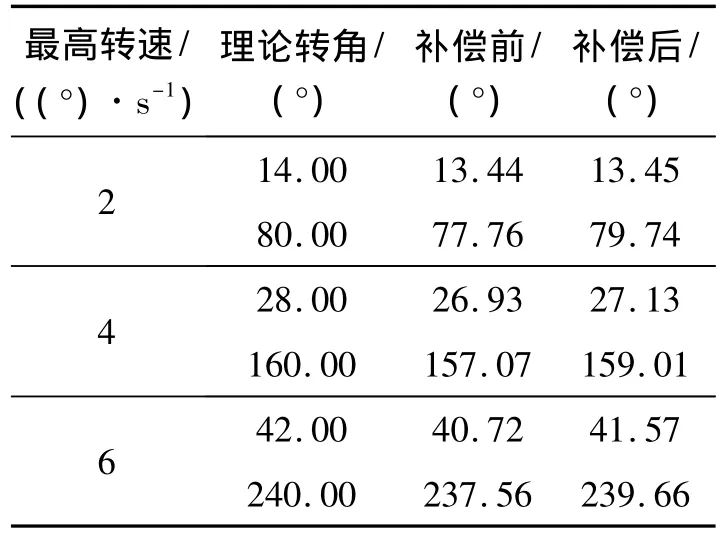
表2 补偿前后转帆角度数据表Table 2 Slewing angle accuracy comparison before and after compensation

2.3 补偿控制后压力特性实验

经过前期仿真、实验研究，风翼回转液压实验台的起动、制动控制采用正弦控制信号，即控制电流应以正弦规律增长/减小，其起动、制动过程压力特性最佳，对液压系统冲击最小［3］。对调速阀进行非线性补偿控制后，其起动、制动压力特性分别如图11所示。

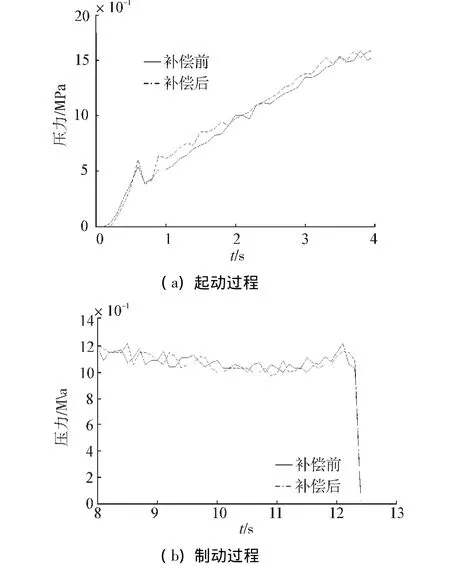
图11 补偿前后起动和制动特性Fig.11 Starting and braking process feature comparison

3 结论

1)通过对翼帆回转实验台的阀控调速开式液压系统的分析及实验研究，得到了翼帆转速与比例调速阀电流的非线性函数关系，并通过实验数据分别建立了升速、降速过程的转速－电流数学模型及其逆模型;

2)采用逆模型前馈非线性补偿方法对调速阀的控制电流进行补偿控制，使用开环控制系统对翼帆回转速度非线性补偿进行实验研究，结果表明，该方法提高了转速的直线度和转帆精度，直线度误差在2‰以内，翼帆转角误差均在1°以内;

3)使用补偿手段，在正弦信号控制下，起动加速、制动减速过程中系统压力特性基本不变;

4)本文采用的逆函数补偿控制是前馈补偿控制的关键步骤，经过分析和实验研究，这种补偿控制对于翼帆回转精度的提高，乃至阀控调速型液压系统的精度的提高都具有十分重要的意义。为了使转帆过程更加精确，可对前馈、反馈或者两者混合控制进行深入研究。

［1］李元奎，张英俊，孙培廷，等.船舶典型远洋航线上风力资源时空分布特征［J］.大连海事大学学报，2010，36 (2):39-41，46.

LI Yuankui，ZHANG Yingjun，SUN Peiting，et al.Temporal and spatial distribution of wind resources around the typical ocean routes［J］.Journal of Dalian Maritime University，2010，36(2):39-41，46.

［2］王宏明，孙培廷，黄连忠，等.基于翼型理论的风帆助航技术分析［J］.船舶工程，2011，33(3):34-37.

WANG Hongming，SUN Peiting，HUANG Lianzhong，et al.The analysis of sail-assisted ship based on aerofoil theory［J］.Ship Engineering，2011，33(3):34-37.

［3］刘绪儒.风翼回转液压系统特性研究［D］.大连:大连海事大学，2013:2-3，46-48.

LIU Xuru.Characteristic research on slewing hydraulic system of wing-sail［D］.Dalian:Dalian Maritime University，2013:2-3，46-48.

［4］林煜翔.风力助航船舶襟翼帆的设计研究［D］.大连:大连海事大学，2013:2-5，13-15.

LIN Yuxiang.Design and research of flap wing sail for windassisted vessel［D］.Dalian:Dalian Maritime University，2013:2-5，13-15.

［5］入沢登美男，王宝姊.装帆商船“新爱德丸”的液压系统［J］.国外舰船技术:特辅机电设备类，1985(5):25-28，41.

TOMIO I，WANG Baozi.The hydraulic system of sail-assisted merchant ship"New AiToku Maru"［J］.Foreign Ship Technology:Special Auxiliary Electro-mechanical Equipment，1985(5):25-28，41.

［6］王国峰，赵永生，范云生.风速风向测量误差补偿算法的研究［J］.仪器仪表学报，2013，34(4):786-790.

WANG Guofeng，ZHAO Yongsheng，FAN Yunsheng.Research on error compensation algorithm for wind speed and direction measurement［J］.Chinese Journal of Scientific Instrument，2013，34(4):786-790.

［7］刘绪儒，黄连忠，林煜翔，等.基于AMESim船舶风翼回转液压系统仿真分析［J］.液压气动与密封，2013(4): 30-34.

LIU Xuru，HUANG Lianzhong，LIN Yuxiang，et al.Analysis of wing-sail hydraulic slewing system based on AMESim［J］.Hydraulics Pneumatics and Seals，2013(4):30-34.

［8］吴根茂，王庆丰，魏建华，等.新编实用电液比例技术［M］.杭州:浙江大学出版社，2006:24，155-157.

WU Genmao，WANG Qingfeng，WEI Jianhua，et al.Electrohydraulic proportional technique in theory and application［M］.Hangzhou:Zhejiang University Press，2006:24，155-157.

［9］赵志强，马冉祺，冯宝辉，等.基于AMESim风翼回转液压系统动态响应分析［J］.大连海事大学学报，2014，40 (1):66-69.

ZHAO Zhiqiang，MA Ranqi，FENG Baohui，et al.Dynamic response of wing-sail slewing hydraulic system based on AMESim［J］.Journal of Dalian Maritime University，2014，40(1):66-69.

［10］JUNG S B，KIM S W.Improvement of scanning accuracy of PZT piezoelectric actuators by feed-forward model-reference control［J］.Precision Engineering，1994，16(1): 49-55.

［11］张元良，刘欣，方加宝，等.压电陶瓷的磁滞现象对位移精度的影响［J］.制造技术与机床，1998(4):7-8，39.

ZHANG Yuanliang，LIU Xin，FANG Jiabao，et al.Hysteresis effect of piezoelectric ceramics on displacement accuracy［J］.Manufacturing Technology＆Machine Tool，1998(4):7-8，39.

［12］舒亮，陈定方，卢全国.一种新的磁滞非线性前馈补偿算法［J］.自动化学报，2009，35(7):953-958.

SHU Liang，CHEN Dingfang，LU Quanguo.A novel algorithm of nonlinear hysteresis feedforward compensation［J］.Acta Automatica Sinica，2009，35(7):953-958.