分子绝对进化速率与物种分歧时间之间的定量关系

李可群

(同济大学 化学系, 上海 200092)

分子绝对进化速率与物种分歧时间之间的定量关系

李可群

(同济大学 化学系, 上海 200092)

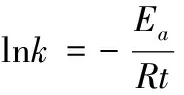
分子进化；绝对进化速率；分子钟；定量关系；系统发育分析

系统发育研究不仅有助重建地球上所有生物体的进化历史，而且还可以揭示生物学领域的一些基本问题。清晰了解各生物物种进化历程及不同物种之间的进化关系，是进一步研究和探索生物学其他学科的基础[1]。

分子系统发育分析大多基于这样一种事实基础: 在各种不同的发育谱系(lineages)及足够大的进化时间尺度中,许多氨基酸或核苷酸序列位点的进化速率是几乎恒定不变的,即基于所谓“分子钟”概念[2]。但在实际工作中，人们发现多数氨基酸和核苷酸序列的“分子钟”都有一定的缺陷, 早在“分子钟”概念提出不久的1971年，Ohta和Kimura就指出分子进化速率并不恒定。相反在不同支系之间存在差异，甚至在同一支系不同进化时间分子进化速率也有变化[3-6]。而对于分子绝对进化速率与物种分歧时间之间的变化关系，不同文献给出了不同甚至是相反的结论。贺福初[7]指出物种分子绝对进化速率随物种分歧时间的减小而下降，即存在“减速进化”现象，文献[8]也指出高等分类元存在进化速率减慢现象。同时实际工作中也发现从鱼类、两栖类、鸟类再到哺乳类，线粒体的分子进化速率是增速的[9]。

准确地估计物种分歧时间和推断其进化历史，是分子进化遗传学和系统发育学的一个重要研究课题[10]。因此了解生物学体系中分子绝对进化速率与物种分歧时间之间的定量关系显得十分重要。本文将利用一些常见“分子钟”分子在这一领域进行初步的探讨。

1 血红蛋白α链体系的研究

1.1 血红蛋白α链绝对进化速率的计算

若假定分子进化速率不变，本文作者给出了分子绝对进化速率的计算公式[11]：

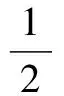
(1)

式(1)中，k1、k2分别为两个同源序列的分子绝对进化速率，t为从共同祖先序列进化的时间，或称两个物种的分歧时间，p为序列比对所得的种间差异率，而k1t、k2t分别为两个同源序列的平均突变概率。d1、d2分别是两个同源序列与共同祖先序列相比的差异位点数，d为两个同源序列中相同位点氨基酸(或核苷酸)不相同的位点数。n0为被比较同源序列氨基酸或核苷酸位点数。为了表述和计算的方便, 本文中分子绝对进化速率的单位采用氨基酸(或核苷酸)位点数/10亿年，进化时间(或物种分歧时间)的单位采用10亿年。

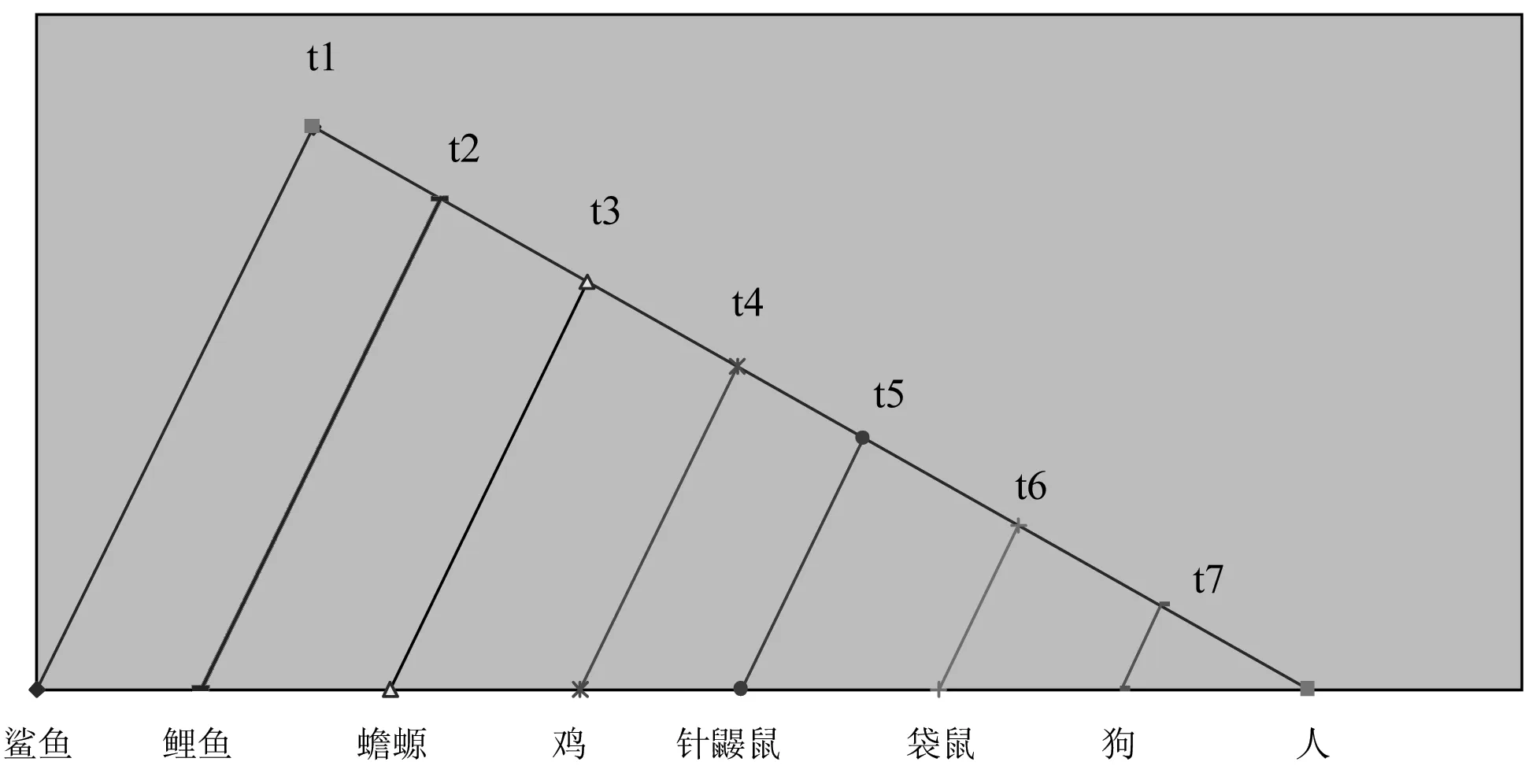
图1 8种脊椎动物的系统进化示意图

我们首先计算了Kimura在其所著的《Theneutraltheoryofmolecularevolution》一书[12]中所举的用来说明分子进化速率恒定的经典体系，即8种脊椎动物(鲨鱼、鲤鱼、蟾螈、鸡、针鼹鼠、袋鼠、狗和人)中血红蛋白α链的绝对进化速率。为了使用最新数据，我们从美国国家生物技术信息中心(NCBI)GenBank数据库中检索了该8种脊椎动物的血红蛋白α链序列数据，它们的Accessionnumber分别为鲨鱼(Callorhinchusmilii,AFM89055.1)、鲤鱼(Cyrinuscarpio,AGJ70090.1)、蟾螈(Tarchagranulose, 0402193A)、鸡(GallusGallus,NP_001004376.1)、针鼹鼠(Tachyglossusaculeatus,P01977.1)、袋鼠(Macropusgiganteus,P01975.1)、狗(Canislupusfamiliaris,P60529.1)和人(Homosapiens,NP_000549.1)。这8种脊椎动物的物种分歧时间来自Kimura的书，它们的系统进化图请参见图1，图中t1至t7分别取0.468、0.423、0.368、0.291、0.232、0.139和0.081，单位为10亿年。

图中8种脊椎动物的血红蛋白α链序列数据使用NCBI提供的ProteinBlast软件进行对齐(align)并计算出物种之间的种间差异率，所得数据见表1。

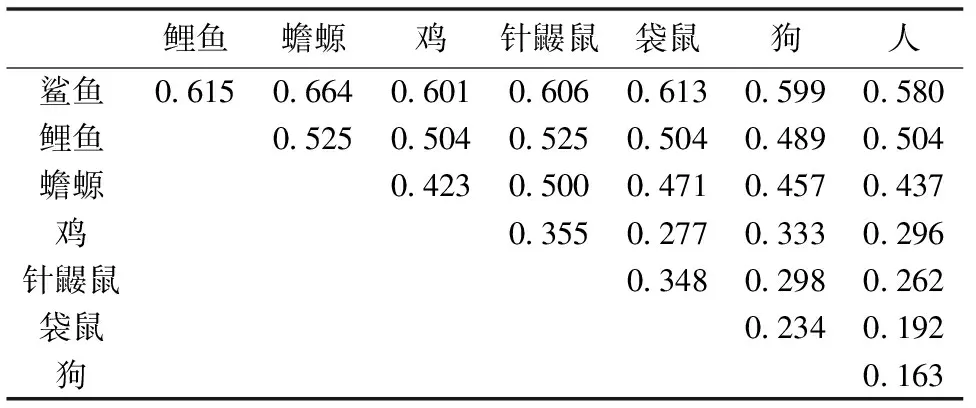
表1 8种脊椎动物血红蛋白α链的比较

由于公式(1)直接求解较为困难，可采用非线性最优化方法求解。若有n种同源序列两两进行比较，则其目标函数为

(2)

式(2)中ki、kj分别为被比较的第i种和第j种同源序列的分子绝对进化速率,pij为它们的种间差异率，tij为它们的物种分歧时间。我们使用优化软件Lingo 11.0计算出8种脊椎动物血红蛋白α链的分子绝对进化速率见表2。

表2 8种脊椎动物血红蛋白α链的分子绝对进化速率

1.2 血红蛋白α链分子绝对进化速率与物种分歧时间的关系

我们在研究分子绝对进化速率与物种分歧时间之间的定量关系时，发现如果将血红蛋白α链分子绝对进化速率与物种分歧时间用下列公式进行拟合

(3)

式(3)中k、t分别为前述的分子绝对进化速率和物种分歧时间，A、B为系数，可发现明显的线性关系，参见图2。

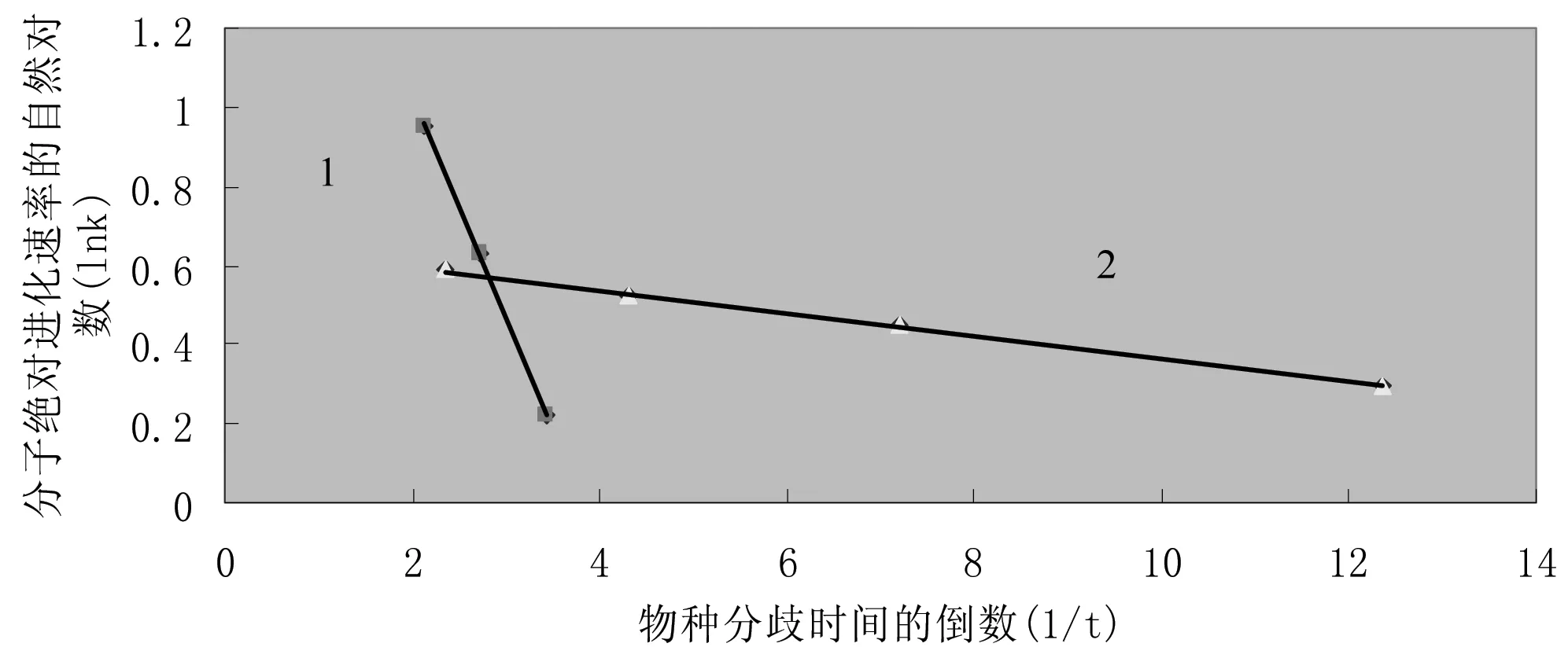
图2 血红蛋白α链分子绝对进化速率与物种分歧时间之间的定量关系Fig 2 Quantitative relationship between hemoglobin α chain molecular

注：图中沿物种分歧时间轴从左至右各点依次为鲨鱼、鲤鱼、蟾螈、鸡、针鼹鼠、袋鼠和人。

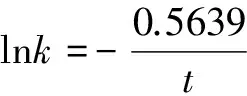
1.3 使用分子绝对进化速率与物种分歧时间之间的定量关系公式拟合数据

为了进一步验证上述定量关系并探究其产生的原因，我们使用式(3)重新拟合其中前7种脊椎动物血红蛋白α链的种间差异率数据。

1.3.1 进化路径各节点区间绝对进化速率之间的关系

若某序列由共同祖先序列进化的路径包含n+1个不同节点，各节点区间的分子绝对进化速率和进化时间分别为k1、k2、……、kn以及t1、t2、……、tn。由于序列分子绝对进化速率计算公式由泊松分布及未突变概率e-kt推导而来[11-12]，不难理解对于包含n段不同节点区间的序列进化路径，存在下列关系式：

(4)

1.3.2 7种脊椎动物血红蛋白α链的种间差异率数据的拟合

由于血红蛋白α链分子为经典的“分子钟”分子，其许多位于不同谱系的分子在较大时间尺度内绝对进化速率数值近似恒定(参见表2)，因此不难理解在7个脊椎动物体系中主干枝和各进化分枝分别可近似视为一个“分子钟”在起作用。以图3示意的两姊妹物种为例说明拟合过程。

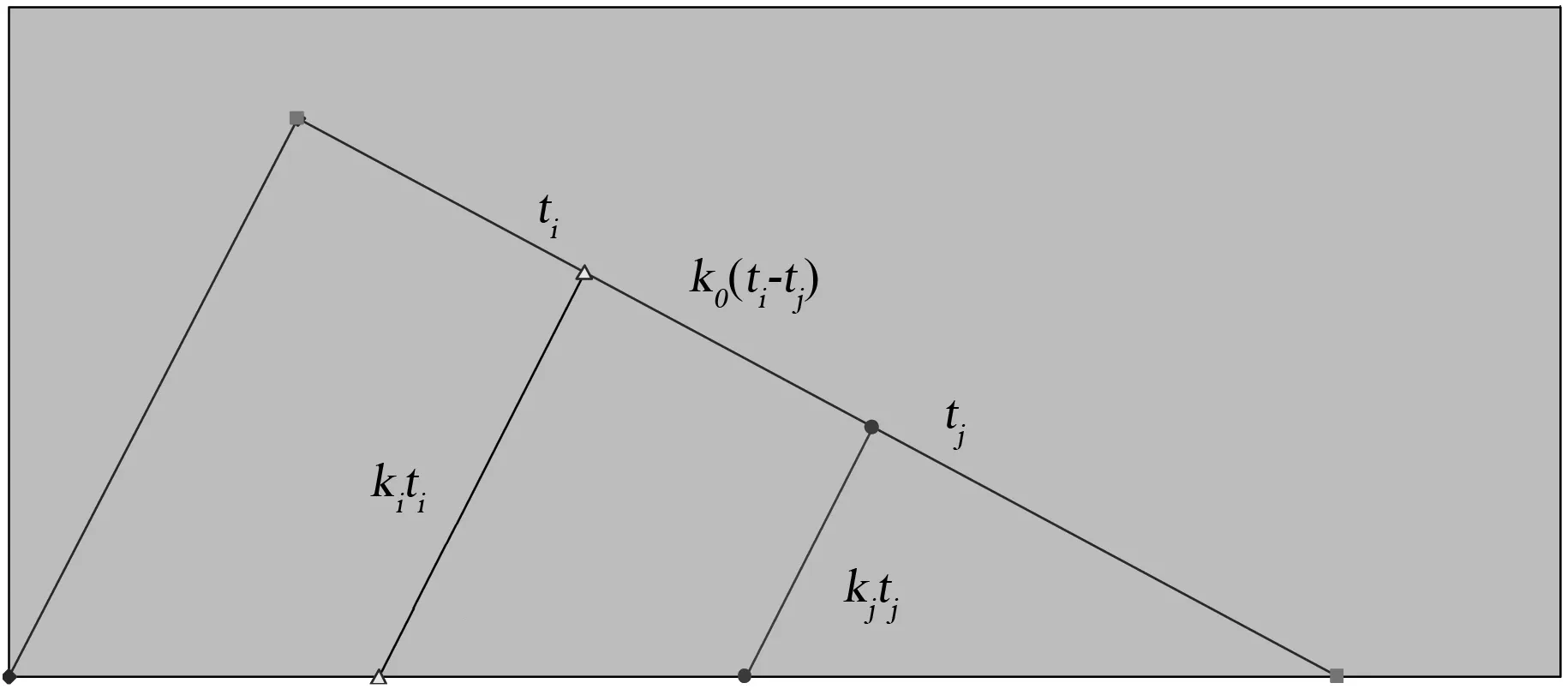
图3 主干枝遗传距离计算示意图

设物种i和j在它们各自进化分枝中分子绝对进化速率分别为ki、kj，而它们的物种分歧时间分别为ti、tj，则它们在各自进化分枝时间段的平均突变概率为kiti和kjtj，将式(3)代入有

(5)

和

(6)

式(5)和式(6)中，Ai、Aj以及Bi、Bj均为系数，由于它们对应着两个不同的姊妹物种，因此系数数值上可能存在差异。而计算物种j时还需包含主干枝ti至tj时间段平均突变概率，该平均突变概率可用下列公式来计算

m=k0j(t0-tj)-k0i(t0-ti)

(7)

式(7)中，t0为主干枝“分子钟”的分歧时间。k0i和k0j分别为主干枝分子在时间t0至ti或tj时间段平均绝对进化速率。将式(3)代入式(7)有

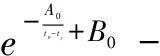
(8)

由于主干枝上可视为同一“分子钟”，故不难理解式(8)中系数A0和B0使用相同数值。将式(8)中eB0用k0替代并移到自然指数项外有

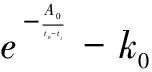
(9)

实际计算表明，式(9)中两个自然指数项上指数绝对值大多较小，因此可近似将两个自然指数项分别用泰勒级数展开并取前两项有

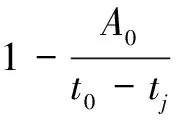
(10)

则物种j在被比较的进化时间段内的总平均突变概率为

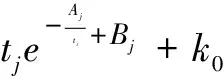
(11)

将式(5)和式(11)所得的平均突变概率代入式(2)目标函数中，同样地我们使用优化软件Lingo11.0 重新拟合了图1中前7种脊椎动物的种间差异率数据。可以得到7种脊椎动物在其各自的进化分枝内的分子绝对进化速率等结果如表3所示，各物种的k0也为它们各自的系数B的自然指数eB。

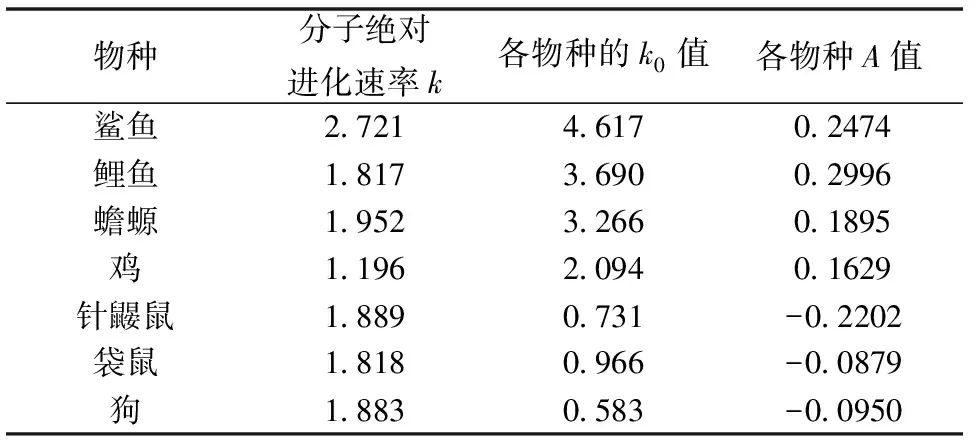
表3 7种脊椎动物体系重新优化的结果

需注意的是, 由于优化过程需满足方程数大于变量数的条件，因此参与计算的物种需大于或等于6种。

1.4 分子绝对进化速率与物种分歧时间之间定量关系公式的物理意义

我们知道化学动力学中化学反应速率常数k与热力学温度T的定量关系可用阿仑尼乌斯公式来表达：

(12)

式(12)中，Ea为化学反应活化能(即活化分子最低能量与反应物平均能量的差值)，R为气体常数，B为与反应体系有关的系数。对比本文公式(3), 可以发现两者公式形式非常相似，而事实上分子进化理论中所称的绝对进化速率严格地应称为绝对进化速率常数，因此我们把公式(3)改写为

(13)

式(13)中Ea为序列位点突变活化能，t为进化时间或物种分歧时间，B为与物种有关的系数，R为与物种无关的常数。Kimura认为氨基酸和核苷酸位点突变为随机过程，即所研究的序列位点上氨基酸或核苷酸可视为独立质点而被其他外来氨基酸或核苷酸质点随机取代，本文作者利用这一思路提出了计算分子绝对进化速率的公式，即本文公式(1), 上述血红蛋白α链以及本文后面所举的例子都表明其计算误差很小，平均残差仅为0.02～0.03左右甚至更小, 这说明将序列位点突变视为质点随机取代过程这种假设是可行的。而取代反应也为化学反应，因此将本文公式(3)改写为式(13)的形式是合理的。

不过，序列位点的突变与化学反应也存在区别，化学反应中，系统热力学温度上升，反应物平均能量增加，可发生化学反应的活化分子百分数增加，从而反应速率常数变大；而序列位点突变中，随着进化时间的增加，突变位点数增加，序列会出现结构张力发生改变等因素使体系能量变化，若体系能量上升，可发生突变的位点百分数增加，使位点绝对突变速率亦即分子绝对进化速率增加，其与进化时间的定量关系公式形式为式(13)；若突变位点数增加导致体系能量下降，可发生突变的位点百分数减小，分子绝对进化速率与进化时间的定量关系公式形式为式(14)

(14)

将式(13)和式(14)改写成指数形式，并用k0替代其中的eB项，则有

(15)

和

(16)

式(15)和式(16)中，当进化时间或物种分歧时间分别趋向无穷大时，分子绝对进化速率k将等于k0，即两式中的k0分别为它们的分子极限绝对进化速率。

由于突变活化能一般为正值，我们不难由式(15)和式(16)来理解本文序言部分提及的随着物种分歧时间的减小而出现分子绝对进化速率增加和减小的两种情形。对于同一进化分枝而言，若属于突变位点数增加时体系能量也增加，即属于式(15)描述的情形，进化时间的减小会导致分子绝对进化速率减小；而若属于突变位点数增加时而体系能量下减，即式(16)描述的情形，进化时间的减小会导致分子绝对进化速率的增加。对于从同一主干枝进化出的姊妹物种，若它们分子的位点突变活化能相差不大，也会出现类似现象，即贺福初提到的所谓“减速进化现象”以及所谓线粒体分子进化的“加速进化现象”。

另外，物种进化时可能会有序列的活化能数值的较大变化，从而出现分子绝对进化速率的较大变化，即出现所谓物种进化时“分子钟”的突然变异[13-14]和物种进化过程可能存在多个串联存在的“分子钟”的现象[15]。

1.5 分子进化过程中“双重分子钟”现象的揭示

如果我们将表3中7种血红蛋白α链的分子极限绝对进化速率与物种分歧时间按式(3)相同形式的公式(17)作图，也可发现明显的线性关系，参见图4。

(17)

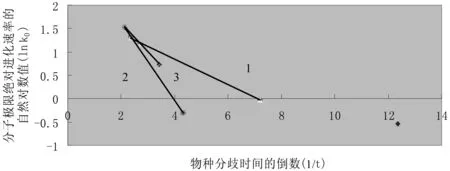
图4 血红蛋白α链分子极限绝对进化速率与物种分歧时间之间的定量关系

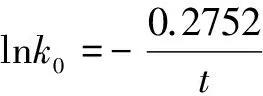
由于物种分子极限绝对进化速率与进化时间或物种分歧时间之间存在上述定量关系，它们也应存在活化能概念和所谓物种分子极限绝对进化速率的极限值。用公式可表达为

(18)

式(18)中Eb为控制物种分子极限绝对进化速率“分子钟”的活化能，k00为分子极限绝对进化速率的极限值。将式(18)代入式(15)有

(19)

式(19)中E0为两个“分子钟”的活化能之和。由该式可以看出，尽管生物分子存在序列位点突变和控制物种分子极限进化速率进化的两个“分子钟”，但表观上看仅表现出一个“分子钟”在起作用，且其极限分子绝对进化速率为k00。不过，当两个活化能数值相差较大时，数值较大的活化能因其对应的指数项数值随时间变化较小而可与数值较小的活化能在二次优化过程中分别求解。

由图4的血红蛋白α链的例子可以看出，7种脊椎动物中存在多组相同的分子极限绝对进化速率的进化活化能，它们的分子极限绝对进化速率的进化极限值k00也各自分别相等，它们具体的生物学意义有待进一步的研究。

2 其他分子体系的研究

为了不失一般性，我们还对其他分子体系进行了研究，取得了相似的结果。

2.1 8种脊椎动物的血红蛋白β链

我们还计算了Kimura在书中为了说明分子进化速率恒定性而举的另一个经典例子，即血红蛋白β链。8种脊椎动物血红蛋白β链的序列数据同样来自于NCBI的GenBank数据库，它们的Accessionnumber分别为: 鲨鱼(Callorhinchusmilii,AFM89007.1)、鲤鱼(Cyrinuscarpio,P02139.1)、蟾螈(Triturusaristatus,P10785.1)、鸡(GallusGallus,NP_990820.1)、针鼹鼠(Tachyglossusaculeatus,P02110.2)、袋鼠(Macropusgiganteus, 690945A)、狗(Canislupusfamiliaris,P60524.1)和人(Homosapiens,NP_000509.1)。同样地使用NCBI提供的ProteinBlast软件进行对齐(align)并计算出物种之间的种间差异率，所得数据见表4。

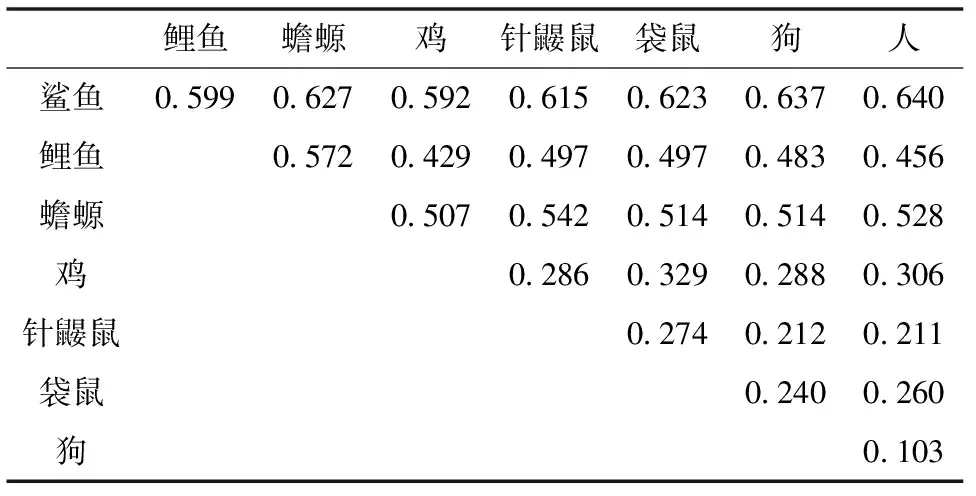
表4 8种脊椎动物血红蛋白β链的比较

我们分别直接使用本文公式(1)和使用公式(3)对表4数据进行了拟合，结果如下。

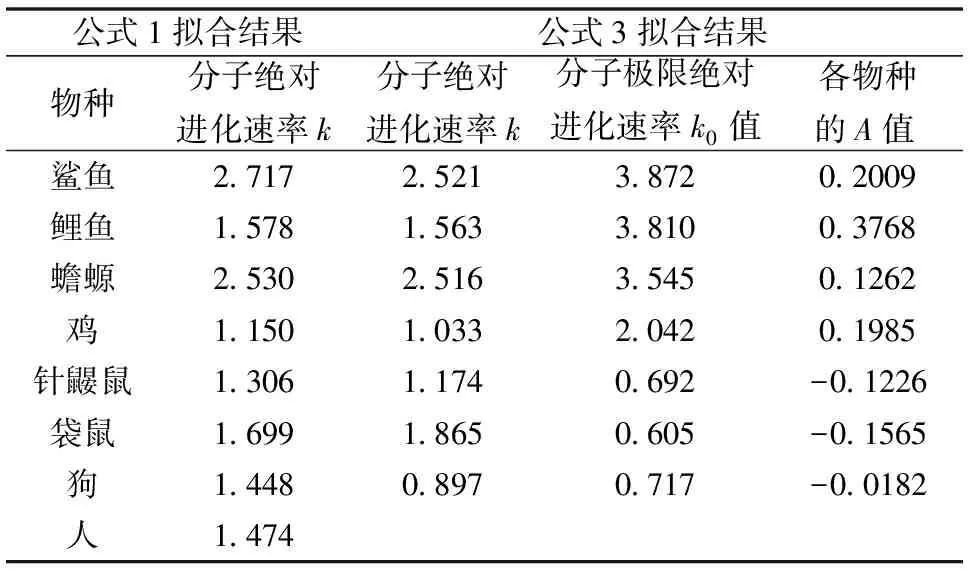
表5 8种脊椎动物血红蛋白β链的优化结果

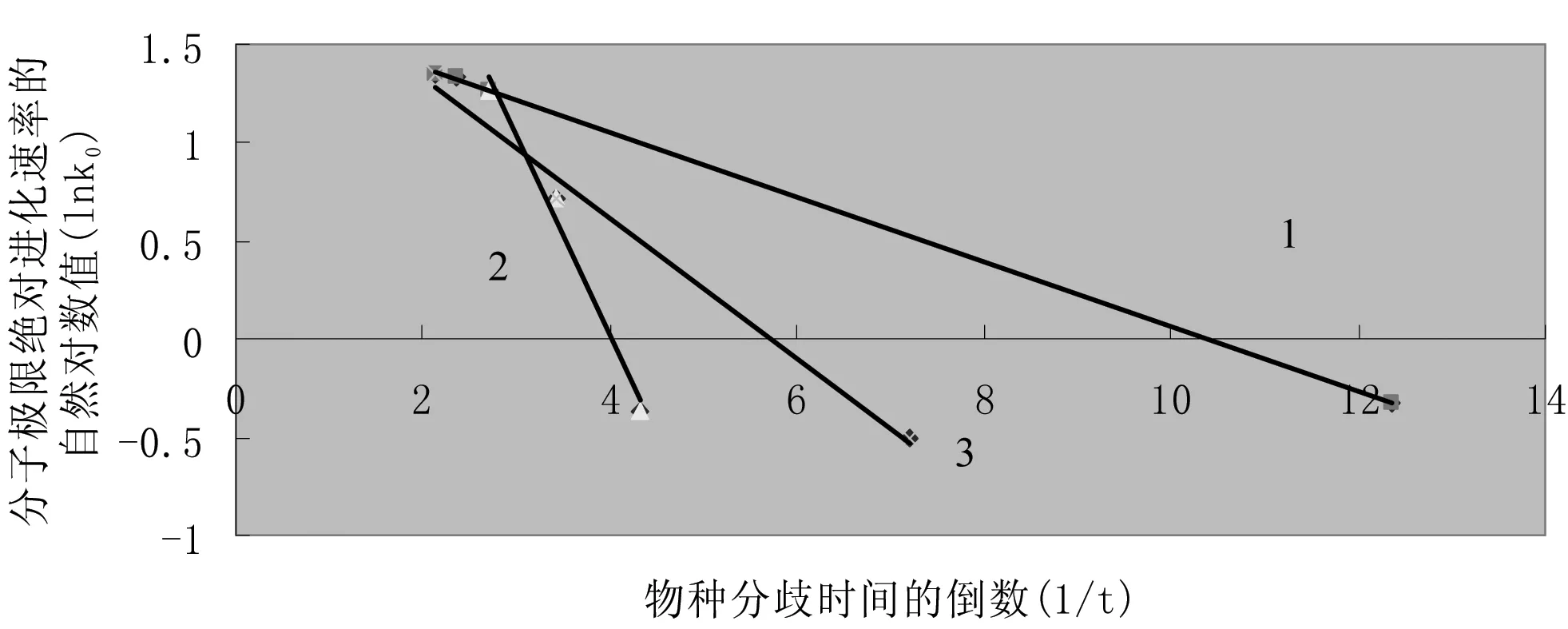
图5 血红蛋白β链分子极限绝对进化速率与物种分歧时间之间的定量关系

Fig5Quantitativerelationshipbetweenhemoglobinβchainmolecularextremeabsoluteevolutionaryratesandtheirtaxadivergencetimes

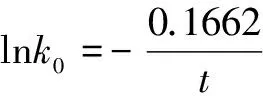
血红蛋白β链体系的计算结果表明生物分子进化确实存在控制序列位点突变和物种分子极限绝对进化速率进化的“双重分子钟”现象。

2.2 其他蛋白质体系

2.3 线粒体核苷酸序列

我们同样也研究了一些线粒体核苷酸序列，具体计算结果请见表6。

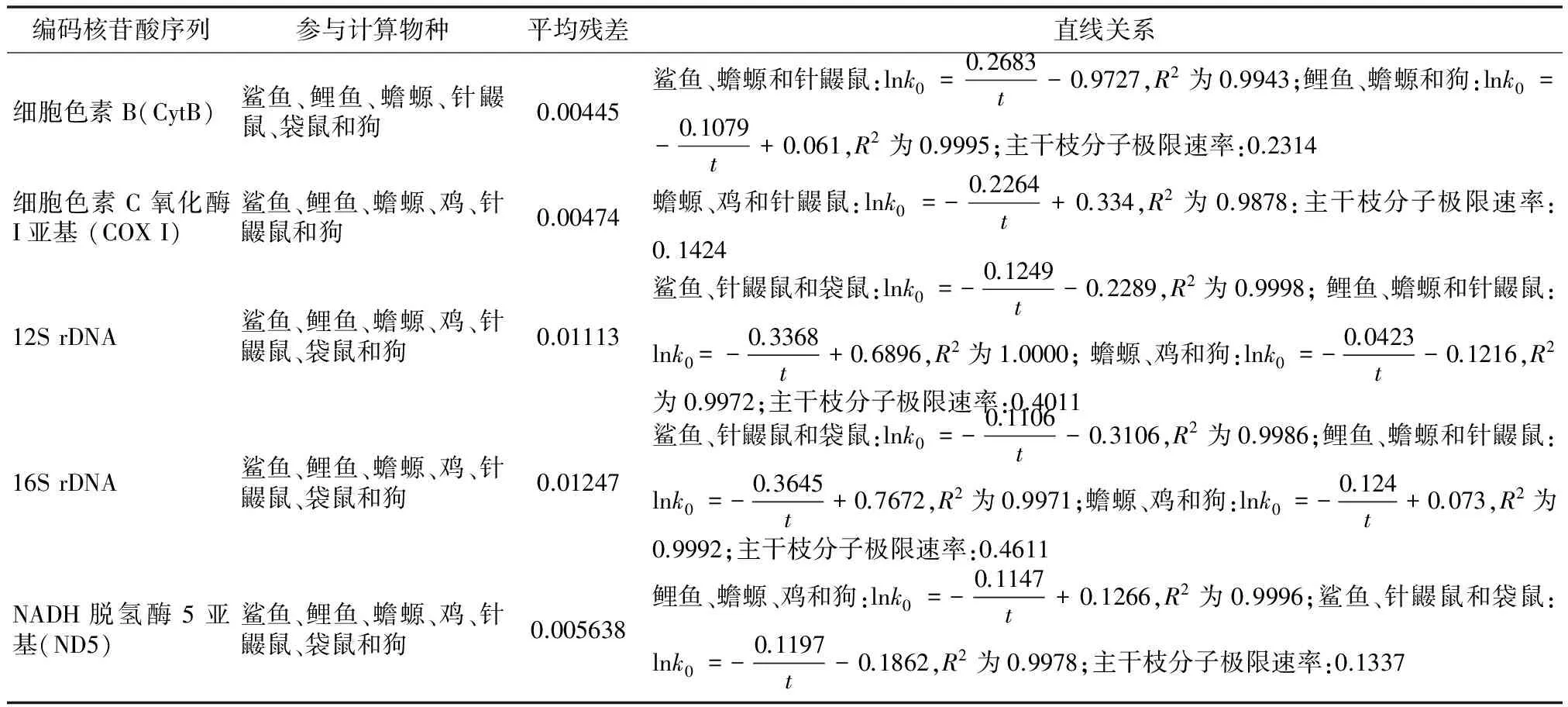
表6 一些线粒体核苷酸序列计算结果

计算过程可能使用的物种及其 accession number 分别为：鲨鱼(Carcharchinus leucas, NC_023522.1)、鲤鱼(Cyprinus carpio, KJ511883.1)、蟾螈(Triturus cristatus, NC_015790.1)、鸡(Gallus Gallus, KF826490.1)、针鼹鼠(Tachyglossus aculeatus, NC_003321.1)、袋鼠(Lagostrophus fasciatus, NC_008447.1)和狗(Canis lupus familiaris, NC_008092.1)。

由表6计算结果可以看出，所得平均残差很小，说明拟合效果较好。同时还可以看出，各体系中均存在一组或多组很好的线性关系，说明“双重分子钟”也存在于线粒体核苷酸序列中。

我们使用本文提出的公式拟合了一些常见“分子钟”分子在7个脊椎动物体系中的蛋白质和核苷酸序列比对数据，它们的平均偏差仅为0.02～0.03左右甚至更小，因此我们认为本文提出的生物分子绝对进化速率与物种分歧时间之间的定量计算公式是符合实验事实的。并且“双重分子钟”现象可能广泛存在于各种蛋白质和核苷酸分子进化体系。

本文给出的公式和结论可为理解多数分子的进化速率在不同谱系甚至同一谱系不同进化时间中存在差异的现象提供帮助，同时也可为解决包括令人困扰的早期生物进化在内的生物系统发育问题提供新的思路和方法。另外，本文还提出了分子位点突变活化能的概念，为研究生物物种进化过程中的能量变化提供了可能。

[1]黎一苇,于 黎,张亚平. 系统发育研究中的“长枝吸收”假象概述[J]. 遗传, 2007, 29(6)： 659-667.

[2]潘星华,傅继梁. 基因的分子进化：原理与方法[J]. 自然杂志, 1995, 17(4):189-193.

[3]柯叶艳,齐文同. 前寒武纪生物起源时间的化石和分子钟研究[J]. 地质论评, 2002, 48(5): 457-462.

[4]Wray G A, Levinton J S， Shapiro L H. Molecular evidence for deep precambrian divergences among Metazoan phyla[J]. Science, 1996, 274: 568-573.

[5]Li W H, Wu C I. Rates of nucleotide substitution are higher in rodent than in man[J]. Molecular Biology and Evolution, 1987, 4(1):74-83.

[6]Ayala F J, Rzhetsky A, Ayala F J. Origin of the metazoan phyla: molecular clocks confirm paleontological estimates[J]. Proc Natl Acad Sci, 1998, 95:606-611.

[7]贺福初. 分子减速进化的普遍性研究[J]. 科学通报,1996, 41(24): 2264-2268.

[8]罗 静. 分子钟及其存在的问题[J]. 人类学学报,2000, 19(2): 151-159.

[9]Adachi A P, Cao Y, Hasegawa M. Tempo and mode of mitochondrial DNA evolution in vertebrates at the amino acid sequence level: Rapid evolution in warm-blooded vertebrates[J]. Journal of molecular evolution, 1993, 36: 270-281.

[10]徐宏发. 分子系统学研究进展[J]. 生态学杂志,2001, 20(3): 41-46.

[11]李可群. 分子绝对进化速率计算公式的推导及应用方法[J]. 高师理科学刊, 2015, 35(1):19-21.

[12]Kimura M. The neutral theory of molecular evolution[M]. Cambridge University Press, Cambridge, 1983.

[13]宫田隆著, 刘绩生译. 什么是分子钟[J]. 世界科学. 1987,11：22-23.

[14]张英培. 分子分类的若干问题[J]. 动物学研究, 1994, 15(1): 1-10.

[15]吕宝忠. 跃入分子水平的群体研究学和进化遗传学[J]. 生物学杂志, 1988, 24(4): 5-8,17.

Quantitative analysis of relationship between absolute evolutionary rates and taxa divergence times

LI Ke-qun

(Department of Chemistry, Tongji University, Shanghai 200092, China)

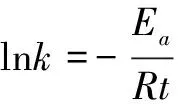
molecular evolution; absolute evolutionary rate; molecular o′clock; quantitative analysis; phylogenetic analysis

2014-08-18；

2014-09-24

李可群，讲师，研究方向为分子遗传进化。

Q

A

2095-1736(2015)02-0070-06

doi∶10.3969/j.issn.2095-1736.2015.02.070