联合格构式构架多向风荷载作用下力学性能分析
程 达
(安徽省电力设计院,安徽 合肥 230601)
大跨度联合格构式构架在国内电力行业相关的工业建筑结构的应用中并不常见。考虑其设计、施工等各方面因素的在国内的局限性,少有应用。
1 本构关系
通过文献[1—8]资料整理及相关工程总结,在统一强度理论基础上,提出了结构钢弹塑性本构模型,此模型不仅适用于拉压强度相同的钢材,而且适用于拉压强度不同的结构钢。
1.1 钢材应力应变理论分析
联合式格构式构架的主要材料为角钢,为了建立合理的三维空间有限元模型,需要定义钢材合理的本构关系。钢材的应力应变经历弹性阶段,弹塑性阶段,塑性阶段,应变强化阶段,见图1。
比例极限σp:直线段的最大应力值。其实严格来说,比σp略高处还有弹性极限,但两者极其接近所以将σp看成是弹性极限。
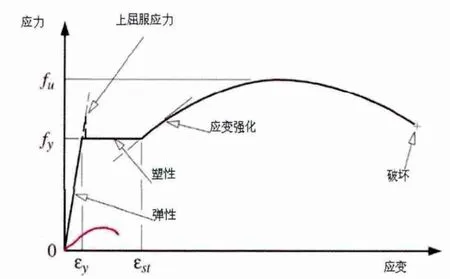
图1 应力应变模型
屈服应力fy:应变ε在σp之后渐渐加大,应力应变成曲线关系一直到屈服点,这是弹塑性阶段,此后应力保持不变而应变持续发展,形成水平线段即屈服平台,这是塑性流动阶段。应力超过σp之后任一点的变形都包括弹性变形和塑性变形两部分,其中塑性变形在卸载后不再恢复,也成为参与变形或永久变形。
1.2 本构模型选取
根据钢材应力应变理论,钢材应力在达到屈服应力fy之前,钢材接近理想弹性体,fy之后塑性应变范围很大而应力保持不变,所以接近理想塑性体。文献[9]对塑性设计的规定就是以钢材是理想弹塑性体的假设为依据,忽略了应变硬化的有利作用。
钢材有屈服平台并且屈服平台末端的应变比较大,这就有足够的塑性变形来保证截面上的应力最终都达到fy,因此一般的强度计算中不考虑应力集中和残余应力。在拉杆中截面的应力按均匀分布计算即以此为基础。从而确立本文格构式构架的钢材可以定义为理想弹塑性模型进行空间有限元模拟计算分析。
2 联合格构式构架模型定义
2.1 荷载定义
通过文献[9,10]采用50年一遇基本风压,将平交及45°风向作用于模型主体结构上,分别对两个平交方向和45°作用方向的作用结果进行比较分析,并根据设计以及实际工程应用的需要,按照构架所受的恒荷载、活荷载(导线拉力、导线覆冰荷载等)、地震反应谱建立不同荷载工况。
2.2 风荷载体型系数μs
本文重点研究了联合格构式构架模型在不同方向风荷载作用下对的力学性能,故不同风向下风荷载体型系数μs是风荷载计算的重要影响系数,文献[11,12]均给出了不同的风荷载体型系数μs计算方法。
针对本文研究的电力工程中的联合格构式构架模型,根据文献[12]中给出的90°风向和对角风向下体型系数的计算方法,通过定义系数:

通过计算不同格构式梁柱的Φ,从而得出联合格构式构架不同杆件的风荷载体形系数μs,并代入文献[12]中风荷载标准值计算公式:

式中:z为高度处的风振系数;βz为风压高度变化系数;μz为基本风压值;w0通过文献[11,12]均可查出。
如前所述,通过文献[12]给出的风荷载体形系数μy的计算方法,可以得出本文研究的联合格构式构架模型在两个平交方向和45°作用方向所需要的可靠的多向风荷载输入数据。
2.3 结构体系布置
构架在各个方向均受不同的导线拉力作用,在满足工艺条件下,选择合理的格构柱和横梁的角钢规格,图2、图3给出了联合格构式构架的单根格构柱局部透视图,构架平面图,三维透视图。

图2 单根格构柱局部透视图

图3 联合格构构架平面布置图
图4 联合格构式构架三维透视图
3 计算结果分析
针对计算结果,挑选联合格构式构架中边跨、中跨10个典型受力构件及节点,在相同的恒荷载及活荷载条件下,分别比较在正交风向1(0°风向),正交风向2(90°风向),斜交风向3(45°风向)三种不同风荷载工况作用下,各柱脚节点及构架主材的应变性能,找出可用于该结构基础设计的控制应力以及验算结构主材是否满足不同风向作用。
3.1 柱脚反力曲线
边跨及中跨柱脚节点拉力、压力分布见图5—图8。

图5 边跨柱脚节点拉力分布曲线

图6 边跨柱脚节点压力分布曲线
通过图5、图6,可知边跨五个柱脚节点反力(拉、压力)由外而内呈现抛物线型分布,边跨中部节点拉压反力最大;三种不同工况作用下,45°风作用下的柱脚反力最大,该工况为设计需考虑的控制工况。

图8 中跨柱脚节点压力分布曲线
通过图7、图8,可知中跨中部柱脚节点或靠近中部拉压反力最大;三种不同工况作用下,45°风作用下的柱脚反力最大,该工况为设计需考虑的控制工况。由于中跨横梁及导线布置,使得中跨柱脚反力最大值并未出现在中间格构柱柱脚节点。
3.2 格构构件应变云图
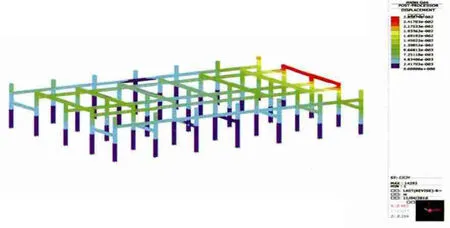
图9 正交风向1应变云图
格构构件应用云图见图9—图11。

图10 正交风向2应变云图

通过图9—图11应变云图,不难发现,在正交风向作用下,结构主材的应变最大,即正交风向作用下的应力可以作为验算构架主材是否满足工程需要的依据;同时,也应考虑斜交风向作用下局部节点及角钢的验算。
4 结语
通过计算结构比较分析,发现本文提及的联合格构式构架,在实际工程中用于基础计算的主导风向应为45°斜交风向:
(1)通过格构柱柱脚反力曲线,发现风向在45°工况下,柱脚拉压力最大;
(2)通过联合格构构件应变云图,可知风向在0°,90°工况下,联合构架式构架构件的应变最大。
(3)用于结构设计的联合格构式构架基础设计的控制应力工况是45°风荷载作用,用于格构构架主材设计的控制应力工况是04°,90°作用。
本文分析比较了三个主导风向作用下的联合格构式构架的柱脚节点反力和应变,三维空间有限元模型有效的模拟了实际工程中的构架,比较得出可用于计算及设计的控制工况反力和应变,弥补了电力工业领域中联合格构式构架在多风向作用下计算分析的欠缺,可以应用推广到类似的工程应用中。
[1]钱令希,等.中国大百科全书:力学篇[M].北京:中国大百科全书出版社,1985.
[2]俞茂宏,何丽南,宋凌宇.双剪应力强度理论及其推广[J].中国科学(A),1985.12(85).
[3]YuMao-hong.Twinshearstressyieldcriterion[J].lnt.J.ofMechanicalScience,1985,25(1).
[4]俞茂宏.双剪理论及其应用[M].北京:科学技术出版社,1998.
[5]赵均海,等.用同一强度理论和同一滑移线场理论求解某些塑性平面应变问题[J].机械工程学报,1999.35(6).
[6]蒋有谅.非线性有限元法[M].北京:北京工业学院出版社,1988.
[7]张汝清,詹先义.非线性有限元分析[M].重庆:重庆大学出版社,1990.
[8]FukumotoY, KusamaH.Localinstabilitytestsofpaltee lementsundercyclicuniaxialloading[J].J.of Struct.Engng,ASCE,1985,111(5).
[9]GB50017-2003,钢结构设计规范[S].
[10]GB50135-2006,高耸结构设计规范[S].
[11]GB5009-2012,建筑结构荷载规范[S].
[12]DL/T5457-2012,变电站建筑结构设计技术规程[S].

