时滞Hopfield神经网络的概周期解❋
张若军, 孟艳双, 卢春阁
(1. 中国海洋大学数学科学学院,山东 青岛 266100;2. 中国海洋大学信息科学与工程学院,山东 青岛 266100;3. 山东交通学院理学院,山东 济南 250357)
时滞Hopfield神经网络的概周期解❋
张若军1, 孟艳双2,3, 卢春阁1
(1. 中国海洋大学数学科学学院,山东 青岛 266100;2. 中国海洋大学信息科学与工程学院,山东 青岛 266100;3. 山东交通学院理学院,山东 济南 250357)
主要研究一类无限区间上的具有S-分布时滞的Hopfield神经网络模型的概周期解问题。一方面去掉激活函数必须满足全局Lipschitz条件的限制,另一方面扩大时滞的应用范围,利用Banach不动点定理和不等式分析技巧,得到了保证所研究的神经网络的概周期解的存在性与全局吸引性的充分条件,并用一个例子说明了所得结果的有效性与可行性。本文结果在一定程度上改善和推广了已有文献的结论。
Hopfield神经网络;概周期解;S-分布时滞;全局吸引性
时滞Hopfield神经网络的动力学性质在神经网络的设计和应用方面发挥了重要的作用[1-2]。在真实的神经系统中,因为生物因素和环境参数随时间波动,所以考虑概周期解比周期解更具有现实意义。近年来,时滞Hopfield神经网络模型的概周期解有一些很好的结果[3-8],但很多早期的文献所考虑的时滞或是离散时滞或是连续时滞,且常假设激活函数是全局Lipschitz的。本文将在去掉激活函数全局Lipschitz条件的限制及扩大时滞的应用范围的情形下,研究一类更广泛的具有S-分布时滞的Hopfield神经网络模型的概周期解问题。
1 模型描述和预备知识
考虑无限区间(-∞,0]上的S-分布时滞Hopfield神经网络模型
(1)
其中:n表示神经元的个数;xi(t)是第i个神经元在t时刻的状态;ci(t)>0表示衰减率,gj表示激活函数;bij(t)表示第j个神经元对第i个神经元的连接权重;Ii(t)是外部输入;Φi(t)是(-∞,0]上的有界连续函数。
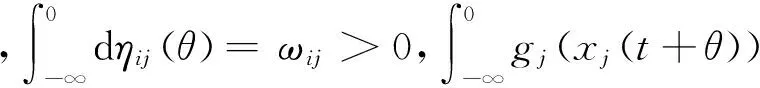



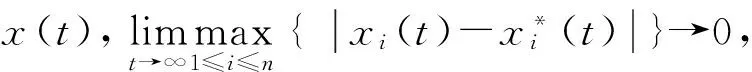

2 主要结果
定理1 若系统(1)满足
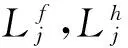



则系统(1)一定存在唯一的概周期解。
证明 对任意φ(t)∈S,考虑系统
(2)



定义映射


从而,对任意φ∈S*,有

由(A1),

把映射T在S*上的限制仍记为T,首先证明映射T是从S*到S*的自映射。事实上,对所有φ∈S*,有

θ))dηij(θ)]ds|≤
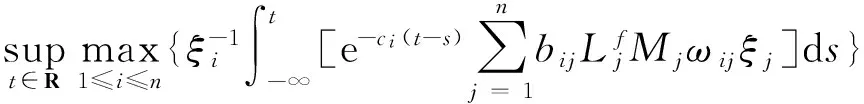
这蕴含了Tφ∈S*。因此,映射T是从S*到S*的自映射。
再证明映射T是压缩映射。事实上,对
∀φ,ψ∈S*,‖T(φ)-T(ψ)‖=

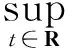
‖φ-ψ‖=q‖φ-ψ‖。
因为0 定理2 假设定理1中的所有条件成立,则系统(1)的概周期解x*(t)是全局吸引的。 x(t)-x*(t),i=1,2,…,n,则有 (3) 显然,系统(1)的解x*是全局吸引的当且仅当系统(3)的零解是全局吸引的。 ‖y(t)‖≤D,∀t>0 (4) (5) 如果(5)式不成立,则必存在t1>0,使得 ‖y(t1)‖=lD (6) ‖y(t)‖ (7) 由(3)式及(A1),(A2),有 此与(6)式矛盾,所以(5)式成立。令l→1,则(4)式成立。 (Ⅱ) 证明系统(3)的零解是全局吸引的。 (8) 由(Ⅰ)知,存在σ≥0,使得 (9) 由上确界极限定义和(9)式,对于充分小的γ>0,存在t2>0,对任意t≥t2,有 ‖y(t)‖≤(1+γ)σ (10) (11) 由(9)~(11)式,当t≥t2+T时,有 所以 (12) 令n=2,考虑如下具有S-分布时滞的Hopfield神经网络模型 易验证定理2的条件满足,故系统(13)存在一个全局吸引的概周期解。 注2 离散时滞和连续时滞互不包含,而S-分布时滞包含了上述两种时滞,更具普遍性。 本文在去掉激活函数全局Lipschitz限制条件以及扩大时滞的范围的情形下,研究了一类具有S-分布时滞的Hopfield神经网络模型的概周期解问题,得到了保证概周期解的存在性与全局吸引性的充分条件,改善和推广了已有文献的结果,并用一个例子说明了所得结果的有效性与可行性。 [1] Chen A P, Cao J D. Existence and attrativity of almost periodic solutions for cellular neural networks with distributed delays and variable coefficients [J]. Appl Math Comput, 2003,134(1): 125-140. [2] 陈安平, 黄立宏. Hopfield神经网络概周期解的存在性和吸引性 [J]. 数学物理学报, 2001, 21A: 505-511. [3] 王林山. 时滞递归神经网络 [M]. 北京: 科学出版社, 2008. [4] Liu B W, Huang L H. Existence and exponential stability of almost periodic solutions for Hopfield neural networks with delays [J]. Neurocomput, 2005, 68: 196-207. [5] Xia Y H, Cao J D, Lin M R. New results on the existence and uniqueness of almost periodic solution for BAM neural networks with continuously distributed delays [J].Chaos Solition Fract,2007, 31(4): 928-936. [6] Stamov G T, Stamova I M. Almost periodic solutions for impulsive neural networks with delay [J]. Appl Math Modell, 2007 31(7): 1263-1270. [7] Zhao H Y. Existence and global attractivity of almost periodic solution for cellular neural network with distributed delays [J]. Appl Math Comput, 2004, 154(3): 683-695. [8] Bai C Z. Existence and stability of almost periodic solutions of Hopfield neural networks with continuously distributed delays [J]. Nonlinear Anal, 2009, 71(11): 5850-5859. [9] 何崇佑. 概周期微分方程 [M]. 北京: 高等教育出版社, 1992. [10]Copple W A. Dichotomies in Stability Theory [M]. Berlin: Springer-Verlag, 1978. AMS Subject Classification: 34K14 责任编辑 陈呈超 Almost Periodic Solutions for Delayed Hopfield Neural Networks ZHANG Ruo-Jun1, MENG Yan-Shuang2,3, LU Chun-Ge1 (1. School of Mathematical Sciences, Ocean University of China, Qingdao 266100, China; 2. College of Information Sciences and Engineering, Ocean University of China, Qingdao 266100, China; 3. School of Science, Shandong Jiaotong University, Jinan 250357, China) In this paper, we investigate the existence and global attractivity of almost periodic solutions for the Hopfield neural networks with S-type distributed delays on an infinite interval. Removing the global Lipschitz conditions of activation functions, and expanding the scope of application of delays, we give some sufficient conditions ensuring existence and global attractivity of almost periodic solutions for the addressed neural networks by applying Banach fixed point theorem and inequality technique. Moreover, an example is given to illustrate the effectiveness of our results. The results of this paper improve and generalize the results in the literature to a certain extent. Hopfield neural networks; almost periodic solutions;S-type distributed delays; global attractivity 国家自然科学基金项目(11171374;11171315);山东省自然科学基金项目(ZR2011AZ001;ZR2011AM003)资助 2013-05-31; 2014-06-20 张若军(1970-),女,副教授。E-mail:zhangru1626@sina.com O175 A 1672-5174(2015)06-128-04 10.16441/j.cnki.hdxb.20130248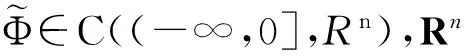
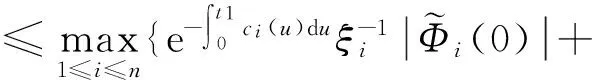





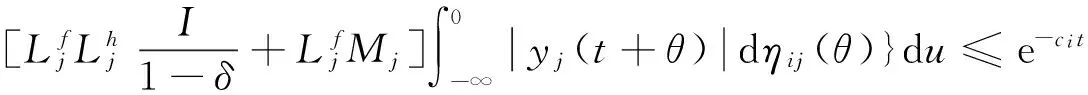


3 例子
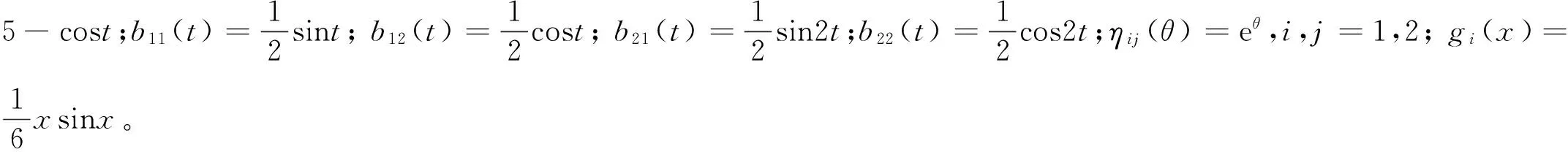

4 结语

