预应力混凝土受弯开裂截面应力计算方法对比

郑毅敏 王怀清 赵 勇，*

(1．同济大学建筑工程系，上海200092;2．同济大学建筑设计研究院(集团)有限公司，上海200092)

1 引言

非预应力筋应力是混凝土受弯构件正截面裂缝宽度验算以及疲劳验算中一项重要计算内容。《混凝土结构设计规范》(GB 50010—2010)［1］(以下简称《规范》)第7．1．3条给出了预应力混凝土构件开裂截面应力分析的基本假定，同时第7．1．4条给出了受拉区纵向钢筋等效应力的简化计算公式。但对于受压区混凝土法向应力图，二者取法不同，其中第7．1．3 条取为三角形，而第7．1．4 条则取为抛物线形。采用不同受压区混凝土法向应力图对计算结果的影响值得研究，特别是当混凝土强度较低或预应力度较大时，预应力混凝土构件在正常使用极限状态下受压区混凝土进入塑性的程度将较大。本文在平截面假定的基础上，推导了混凝土本构模型取为三角形和抛物线形时非预应力筋应力计算公式，通过算例对不同算法的结果进行了对比与分析，并讨论了折减弹性模量的取值。

2 计算方法的建立

2．1 基本假定

《规范》第7．1．3条对开裂截面应力计算的基本假定为:① 截面应变保持平面;②受压区混凝土的法向应力图取为三角形;③不考虑受拉区混凝土的抗拉强度;④采用换算截面。其中对第③条、④条假定已为业界普遍认可，但对第①条、②条仍然存在争议。

在平均应变层面以及受弯承载能力极限状态下，正截面符合平截面假定已成共识，但对于正常使用极限状态下，国内外关于平截面假定仍存有不同看法。开裂截面的平截面假定是最新一版《规范》新增的内容，《规范》过往版本并未明确该假定。苏联在20世纪五六十年代的研究认为，开裂截面应变不符合平截面假定［2］。而太原理工大学［3］和中国建筑科学研究院［4］通过对钢筋混凝土梁和部分预应力梁的疲劳性能试验，得出了可以采用平截面假定计算受弯构件正截面应力的结论。文献［2］指出:采用平截面假定的计算结果与试验结果符合较好，间接论证了平截面假定的成立。美国规范 ACI 318［5］、欧洲规范 EN1992 －1 －1［6］以及模式规范 MC2010［7］均采纳了平截面假定。文献［8］也采用了平截面假定，但在文献［9］中推导相关计算公式时未明确提及是否采用了平截面假定。

对受压区混凝土法向应力图的选取主要有两种模式:

(1)取受压区法向应力图为三角形(以下简称“三角形模式”)。《规范》第7．1．3条取了三角形模式，但未明确三角形斜率的取值，仅在相应条文说明中指出，“计算换算截面时，必要时可考虑混凝土塑性变形对混凝土弹性模量的影响”。文献［9］在推导开裂截面应力计算公式时，也取混凝土法向应力图为三角形，且斜率取为混凝土弹性模量Ec。

(2)考虑混凝土弹塑性的影响取受压区法向应力图为抛物线形(以下简称“抛物线模式”)。我国《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG DT62 －2004)［10］和《水工混凝土结构设计规范》(SL 191－2008)［11］采用抛物线模型计算预应力混凝土受弯开裂截面的内力臂。文献［10］在建立开裂截面受拉钢筋应力的近似计算公式时，也取抛物线形法向应力图，并通过拟合分析来近似确定内力臂，该思路已为《规范》第7．1．4条所采纳。美国规范ACI 318［6］对两种模式均有提及，但未明确采用何种模式。

2．2 开裂截面应力计算简图

计算预应力混凝土受弯开裂截面的钢筋应力时，可将截面视为偏心受压的钢筋混凝土截面［9］。此时，作用于截面的等效压力 Np0及该力距预应力筋合力点的距离为e—，可按下式计算:

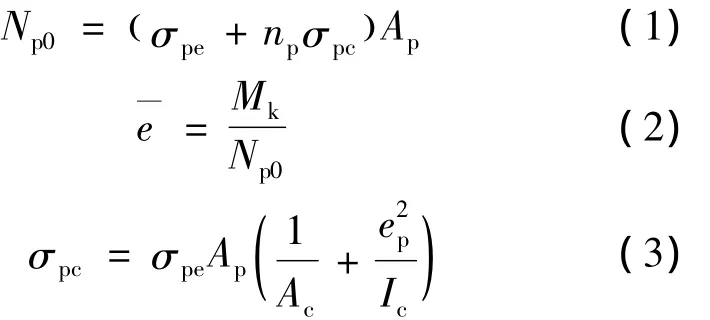
式中，σpe为预应力筋有效应力，np为预应力筋弹性模量Ep与混凝土弹性模量Ec之比，np=Ep/Ec，σpc为由预加力产生的混凝土法向应力，Ac、Ic分别为混凝土换算截面面积和惯性矩，Mk为外弯矩。

根据平截面假定，可得图1所示的预应力混凝土受弯开裂矩形截面应力计算简图。图中，b，h，x，φ分别为截面宽度、高度、受压区高度和曲率;x1，x2轴分别为截面形心轴和开裂截面中性轴;Ap，hp，ep，εp，Δσp分别为预应力筋的面积、几何中心到截面顶部的距离、偏心距、应变和应力增量;As，hs，εs，σs分别为非预应力筋的面积、几何中心到截面顶部的距离、应变和应力;εc，σc分别为顶面混凝土的压应变和压应力;d，z分别为顶面、受拉区纵筋合力点至混凝土压应力合力作用点的距离。

图1 开裂截面应力计算简图Fig．1 Calculation diagram of cracked section

2．3 三角形模式下的计算公式

由图1(c)，可建立力和力矩平衡方程，经整理可得受压区高度x的方程［9］:

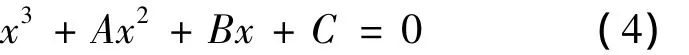
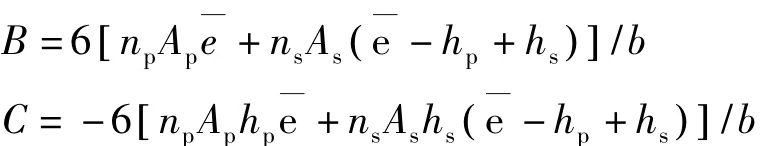
其中，ns=Es/Ec，Es为非预应力筋的弹性模量。

同时，可得到εc的计算公式:

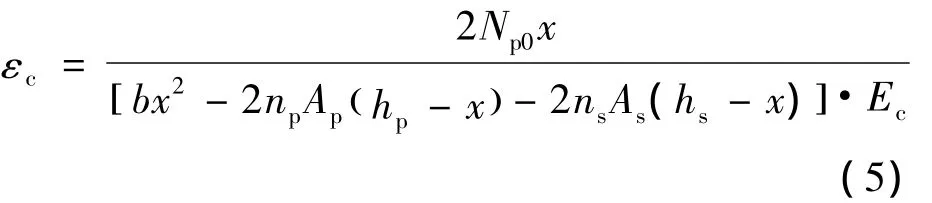
进而由图1(b)，可以建立出 σs、Δσp与 εc的关系，即:

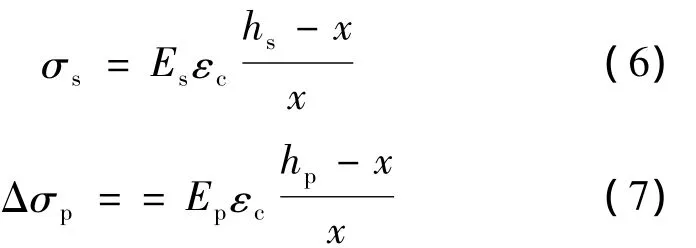
2．4 抛物线模式下的计算公式推导

参考《规范》第6．2．1条关于正截面极限承载能力计算假定中受压区混凝土法向应力模型，对强度等级不超过C50的混凝土，其单轴受压本构模型取为二次抛物线，即:

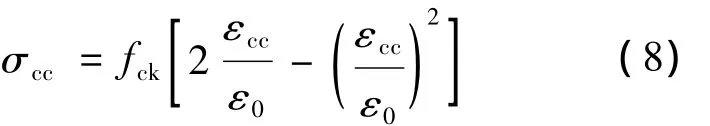
式中，σcc为混凝土压应力;εcc、fck、ε0分别为混凝土轴心抗压强度标准值、压应变、受压弹性极限应变，取 ε0=0．002。

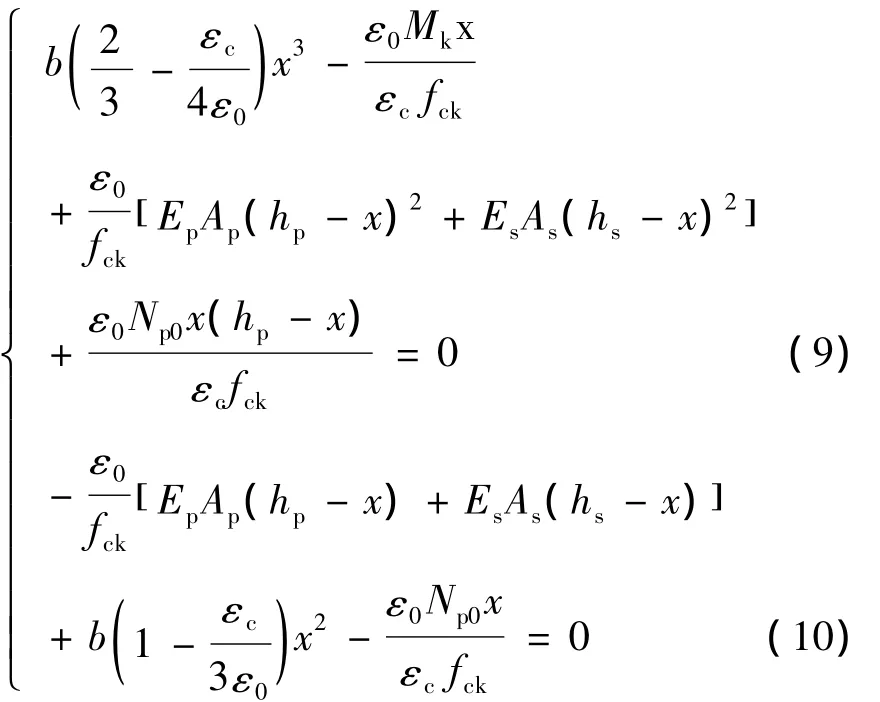
由图1(d)，可建立力和力矩平衡方程，经整理可得关于x和εc方程组:采用数值分析方法求解上述方程组，并将x和计算结果代入式(6)即可求得σs。

2．5 《规范》简化公式

《规范》第7．1．4条给出预应力混凝土受弯构件开裂正截面的受拉纵筋合力点处的等效应力σs0计算的简化公式。为便于比较，需将σs0转化成σs和 Δσp，并取受力纵筋合力点有效高度为由图1(d)可知:

将式(11)、式(12)与式(6)、式(7)联立方程组，可以求解出σs和Δσp。

3 算例分析

3．1 算例概况

从10个预应力工程中选取了20个框架梁截面，其中非预应力筋均为HRB400级钢筋，预应力筋均采用φs15．2钢绞线，其抗拉强度标准值fpt，k=1 860 MPa，其他主要截面参数见表1。利用20个截面参数，通过3个算例对比不同计算模式的钢筋应力差异及分析主要的影响参数。算例1－3中抛物线模式、三角形模式和《规范》［1］简化公式算得的钢筋应力分别记为 σspi，σssi和 σsgi(i=1，2，3)，相对偏差记为:

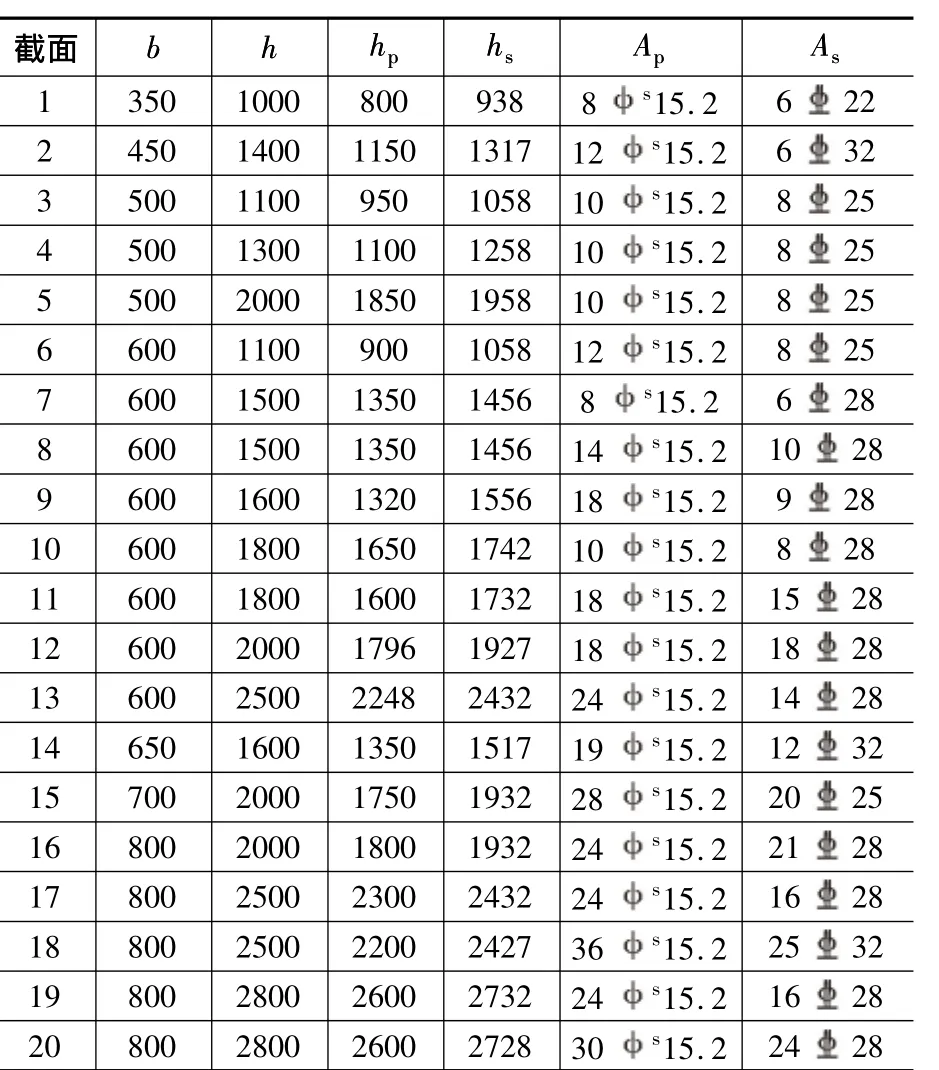
表1 算例主要截面参数Table 1 Main sectional parameters

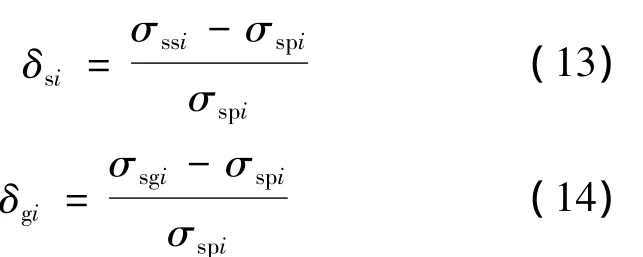
计算钢筋应力时，分别取了 Mk=0．55Mu，Mk=0．65Mu和 Mk=0．75Mu三个工况，其中，Mu为按照《规范》［1］第6．2．10 条计算的受弯承载力。

3．2 算例分析

【算例1】令混凝土强度等级为 C40，σpe=1 100 MPa。

算例1的计算结果如图2所示，可见:

(1)与 σsp1相比，σss1偏小，δs1在 －14．5% ～－4．1%之间，平均为 －8．5%;

(2)与 σsp1相比，σsg1偏大，δg1在 0 ～42．7%之间，平均为14．7%，且较为离散;

(3)随着Mk/Mu的增大，δs1没有明显变化，δg1有所下降，但离散性仍较高;

(4)δs1和 δg1的差值在 －49．6% ～ －7．6%之间，平均为－22．3%。

因此，根据《规范》第7．1．3 条和7．1．4 条计算的钢筋应力有较大偏差，可能会影响裂缝宽度或疲劳应力验算结果，建议《规范》应有必要的说明或修正。

图2 例1计算结果Fig．2 Calculation results of example 1

【算例2】令混凝土强度等级为 C50，σpe=1 100 MPa，以研究混凝土强度等级对计算结果的影响。

算例2的计算结果如图3所示，由图2和图3可见，在提高混凝土强度后:

(1)与 δs1相比，δs2减小，在 －8．5% ～ －2．3%之间，平均为 －4．5%;

(2)与δg1相比，δg2有所增大，且更为离散，在3．4% ～47．3%之间，平均为18．2%。

因此，当混凝土强度较高时，三角形模式和抛物线模式的计算结果差别不大，但《规范》［1］简化公式的结果会有较大差别，其适用性值得进一步研究。

图3 例2计算结果Fig．3 Calculation results of example 2

【算例3】令混凝土强度等级为C40，σpe=750 MPa，以研究预压力大小对计算结果的影响。

算例3的计算结果如图4所示，由图2和图4可见，随着预压力的降低:

(1)相比 δs1，δg3有所减小，在 － 7．5% ～－3．0%之间，平均为 －4．8%;

(2)相比 δg1，δs3有所减小，离散程度下降，在0 ～16．1%之间，平均为5．7%。

因此，对于预压力较大的情况，采用不同模式的计算结果差别不大，但对于《规范》简化公式所适用的预压力范围值得进一步研究。

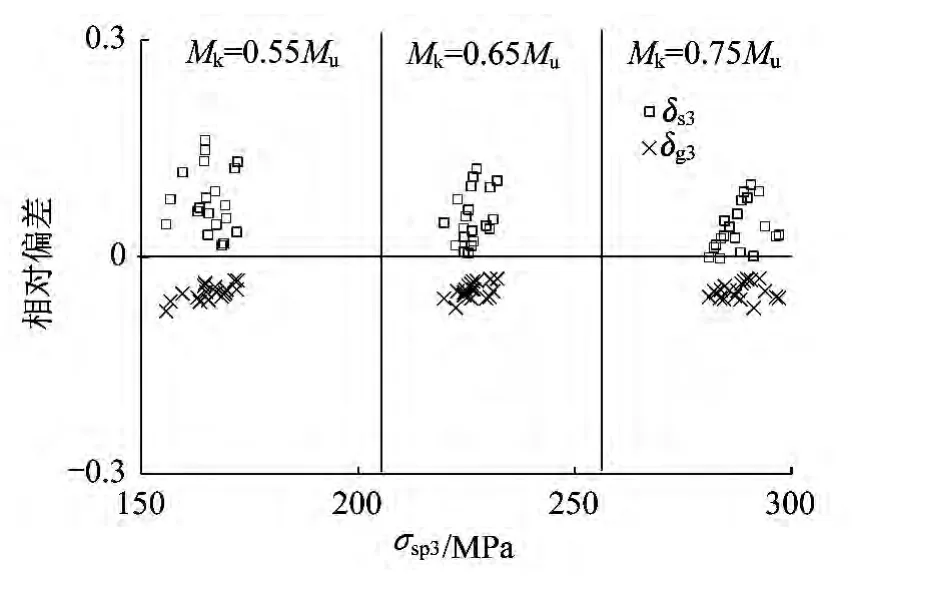
图4 例3计算结果Fig．4 Calculation results of example 3

4 折减弹性模量法

采用抛物线模式时，求解相应方程组较为困难，而采用三角形模式时则可用降阶法进行简化计算［9］。在工程应用中，一般采用折减混凝土弹性模量的方法，以考虑混凝土塑性的影响。文献［12］建议取折减系数为0．65。

图5 折减弹性模量法计算结果Fig．5 Calculation results with reduced modulus of elasticity

对于本文的3个算例，当Mk为0．55Mu时，钢筋应力较小，可以认为混凝土基本处于弹性状态;在 Mk为0．65Mu和0．75Mu两种工况下(相应的 σs≥120 MPa)，当取 α =0．65 时，计算结果相对偏差在 －4．8% ～2．0%之间，平均为 －2%。通过进一步计算得知，当取α=0．60时，相对偏差在－3．7% ～2．9%之间，平均接近零，其计算结果如图5所示。因此，根据本文算例结果，建议取混凝土折减弹性模量为0．6Ec。

5 结论与建议

对正常使用极限状态下预应力混凝土受弯开裂正截面应力，本文通过算例，对比了按《规范》第7．1．3 条和第 7．1．4 条规定计算的结果，并对比了在平截面假定下，三角形模式和抛物线模式计算结果的差异。根据本文算例结果，得到以下结论与建议:

(1)采用三角形模式，且斜率为Ec时，计算结果相比采用抛物线模式的偏低，且随着混凝土强度提高，平均相对偏差从－8%减小至－5%，随着预压力减小，平均相对偏差从－8%减小至－5%。

(2)采用《规范》第7．1．4条简化公式，计算结果比抛物线模式的偏大，平均相对偏差为15%，且离散性较大，计算结果的离散性和相对偏差随着外弯矩的增大而减小，但随着混凝土强度的提高和有效预应力增大而增大。

(3)对用于预应力混凝土构件裂缝宽度验算的钢筋应力，建议采用抛物线模式计算，当采用三角形模式时，建议采用折减弹性模量法，根据本文算例结果，折减系数可取为0．6Ec，且有必要对折减系数做进一步深入研究。

(4)按《规范》第7．1．3 条和7．1．4 条的计算结果可能存在较大差异，建议《规范》作出必要的说明或修正，特别是对混凝土强度较高的情况。

致谢 中国建筑科学研究院白生翔研究员对本文提出了宝贵的意见和建议，特在此表示由衷感谢!

［1］ 中华人民共和国住房和城乡建设部．GB 50010—2010混凝土结构设计规范［S］．北京:中国建筑工业出版社，2010．Ministry of Housing and Urban-Rural Development of the People’s Republic of China．GB 50017—2010 Code for design of concrete structures［S］．Beijing:China Architecture and Building Press，2010．(in Chinese)

［2］ 白生翔，李引擎．钢筋混凝土和预应力混凝土受弯构件受拉钢筋应力的简化计算(一)［J］．工业建筑，1988，18(1):42-47．Bai Shengxiang，Li Yinqing．The simplified method of calculating steel bar stress in RC and prestressed RC bending members(Part I)［J］．Industrial Construction，1988，18(1):42-47．(in Chinese)

［3］ 田种德，李慧民，顾传霖．钢筋混凝土受弯构件正截面疲劳验算方法的研究［M］∥钢筋混凝土结构研究报告选集(2)．北京:中国建筑工业出版社，1981:235-254．Tian Zhongde，Li Huimin，Gu Chuanlin．Normal section fatigue assessment method of RC bending moments［M］∥Anthology of the Reinforced Concrete Structures Research Reports(Part 2)．Beijing:China Architecture and Building Press，1981:235-254．(in Chinese)

［4］ 沈在康，孙慧中，马坤贞．允许出现裂缝的部分预应力混凝土梁的疲劳性能［M］∥钢筋混凝土结构研究报告选集(2)．北京:中国建筑工业出版社，1981:184-234．Shen Zaikang，Sun Huizhong，Ma Kunzhen．Fatigue properties of cracked partially prestressed concrete beam［M］∥Anthology of the Reinforced Concrete Structures Research Reports(Part 2)．Beijing:China Architecture and Building Press，1981:184-234．(in Chinese)

［5］ ACICommittee 318．Building code requirements for structural concrete(ACI 318－11)and commentary(ACI 318R-11)［S］．American Concrete Institute，Farmington Hills，Michigan，2011．

［6］ British Standards．BS EN1992-1-1:2004:Eurocode2:design of concrete structures-Part 1-1:General rules and rules for buildings［S］．London:British Standards Institution，2004．

［7］ International Federation for Structural Concrete．Model code 2010［S］．Lausanne，2012．

［8］ 赵国藩，刘亚平，陈永春．部分预应力砼梁截面应力计算的分区降阶逼近法［J］．建筑结构学报，1987，8(2):55-66．Zhao Guofan，Liu Yaping，Chen Yongchun．Sectional stress calculation of partially reinforced concrete beam with method of reduction of order［J］．Journal of Building Structures，1987，8(2):55-66．(in Chinese)

［9］ 丁大钧，蓝宗建，金芷生，等．矩形、T形和工字形截面钢筋混凝土偏心受压构件刚度、裂缝的试验研究和计算建议［J］．建筑结构学报，1983(2):11-20．Ding Dajun，Lan Zongjian，Jin Zhisheng，et al．Experimental study and calculation suggestions about stiffness and crack of reinforced concrete eccentric compression members with rectangle and T-shaped and I-shaped section［J］．Journal of Building Structures，1983(2):11-20．(in Chinese)

［10］ 中华人民共和国交通部．JTG D62—2004公路钢筋混凝土及预应力混凝土桥涵设计规范［S］．北京:中国建筑工业出版社，2004．Ministry of Transport of the People’s Republic of China．JTG D62—2004 Code for design of highway reinforced concrete and prestressed concrete bridges and culverts［S］．Beijing:China Architecture and Building Press，2004．(in Chinese)

［11］ 中华人民共和国水利部．SL191—2008水工混凝土结构设计规范［S］．北京:中国水利水电出版社，2008．Ministry of Water Resources of the People’s Republic of China．SL 191—2008 Design code for hydraulic concrete structures［S］．Beijing:China Water Power Press，2008．(in Chinese)

［12］ 住房和城乡建设部标准定额研究所．热轧带肋高强钢筋在混凝土结构中应用技术导则［M］．北京:中国建筑工业出版社，2010 Ministry of Housing and Urban-Rural Development of the People’s Republic of China．Technical guidelines for application of high strength hot rolled ribbed bars in concrete structure［M］．Beijing:China Architecture and Building Press，2010．(in Chinese)