基于磁弹效应的预应力钢绞线全量应力监测实验研究

庞国英 董传智 段元锋，* 周超波

(1．台州市公路管理局，台州318000;2．浙江大学建筑工程学院，杭州310058;3．杭州健而控科技有限公司，杭州310030)

1 引言

预应力混凝土结构是在结构构件受外力荷载作用之前对构件施加压力，使荷载作用时截面受拉区域先存在压应力的混凝土结构。与普通混凝土结构相比它具有结构安全可靠、节约材料、自重较小、抗裂性好和刚度大等优点，现已广泛应用于桥梁、大坝、高速公路、民用建筑等结构中，是现代土木工程领域发展速度最快、用途最广、最具发展潜力结构形式之一［1］。

钢绞线作为预应力结构中的关键受力构件，其受力状态直接影响预应力结构的适用性和安全性。预应力钢绞线在张拉及桥梁运营过程中，由于材料性能、施工状况和环境条件等因素的影响，混凝土桥梁会产生不可预见的预应力损失，从而导致预应力水平的降低和预应力分布的不均匀。

一旦预应力构件中的钢绞线预应力失效，混凝土结构构件将可能在表面未有征兆的情况下很快发生破坏，对于连续多跨的无粘结预应力结构，一旦钢绞线预应力失效，将导致余跨的钢绞线预应力一起失效，从而使结构的承载能力下降，使结构处于不良的工作状态，给桥梁结构安全带来潜在危害。针对预应力结构中钢绞线的应用现状，亟需一种检测技术，对钢绞线中的有效预应力进行实时监测，以便准确地了解和掌握预应力结构的应力状态和变化规律，对出现问题的预应力结构及时进行维修或更换，避免由于钢绞线中的应力损失导致整个结构的破坏，造成重大的经济损失和人身伤害。

预应力钢绞线的应力监测有其特殊性:①位于混凝土内部，工作空间狭小;②跨度大、距离长，需进行准分布监测才能获取全面准确的预应力状态;③初始张拉应变水平高，损失应变量相对较小，采用应变测量法效果不佳;④桥梁结构的寿命一般为几十年，需要对持久应力进行长期监测。目前常用的电阻应变片、振弦式应变仪［2］、光纤光栅应变仪［3］、钢绞线传感器［4］等，都无法或难以实现对在役预应力钢绞线应力绝对量(而非相对变化量)的无损监测;由于预应力混凝土桥梁的预应力钢绞线其边界条件、应力幅值、作业空间等与拉索、吊杆等柔性结构有明显区别，因此振动频率法［5，6］也不适用于混凝土桥梁的预应力筋的应力测量;超声导波检测［7］虽具有理论上的可行性，但试验表明其测试结果很不稳定，目前尚停留在理论探索和试验研究阶段。要实现对在役预应力混凝土桥梁的预应力筋实际应力的无损检测，必须结合预应力筋自身的特点寻求新的方法。

磁通量传感器［8］是一种新型的应力监测方法，它不仅能够对预应力钢绞线进行无损、长久、稳定的应力监测，更重要的是能够适应预应力钢绞线特殊的施工工况，是一种可以替代前述各种监测手段的好方法，磁弹效应法已然成为国内外研究的热点［8－12］。

虽然磁通量索力传感器已经应用于实际工程的索力测量中，但是其中的许多关键问题仍需解决和完善，如磁弹索力传感器系统的精细建模与系统优化，实验研究的完善，磁屏蔽的改进和测量精度的提高等。在目前的工程案例中，如江阴大桥［10］、南京长江二桥［11］、南京葫芦顶大桥和天津永和大桥［12］，都是对大跨度缆索桥的拉索或吊杆进行测量，其周围铁磁环境相对简单。而钢绞线周围铁磁环境复杂，需要进行专门的实验研究，以确定传感器的抗铁磁环境干扰能力。目前关于基于磁弹效应的钢绞线应力监测实验研究未见报道。

本文基于铁磁材料磁弹效应(即钢绞线在外力作用下其磁特性变化)，通过测量钢绞线的磁特性参数来测量其应力。对单根钢绞线周围有无其他钢绞线两种情况进行实验研究，对钢绞线周围铁磁环境的影响程度进行定量。

2 工作原理及系统组成

铁磁性材料可以实现磁与众多物理量的相互转换，其中的磁—机相互转换功能是将机械量转换成磁学量或反之。实现磁—机转换的核心是材料的磁弹效应(或逆磁致伸缩效应或压磁效应)。所谓的磁弹效应是指铁磁性材料受到机械应力作用时，其材料的导磁性发生改变，尤其是磁导率发生变化的现象［13］。

在被测钢构件上缠绕两个线圈，分别为励磁线圈和测量线圈，在励磁线圈组成的回路中通过变化的电流，通过测出测量线圈两端的感应电压，可以推算被测构件磁导率的变化，装置如图1所示。

置于磁场中的钢构件的感应电压积分值与铁磁材料的增量磁导率关系［14］:

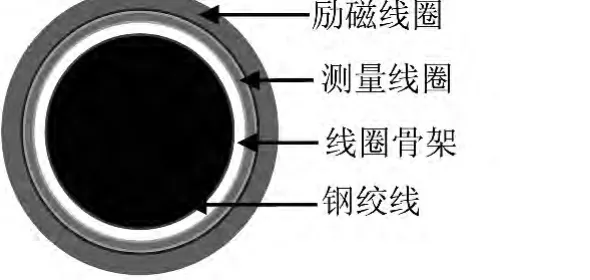
图1 线圈截面示意图Fig．1 The diagram of the coil’s cross-section

式中，μinc为增量磁导率;μ0为空气磁导率;Uout为磁场中有铁磁材料时的励磁时间内感应电压积分有效值;U0为磁场中无铁磁材料时的励磁时间内感应电压积分有效值;SA为测量线圈包裹的面积;SB为钢构件的横截面积。

最终得到应力与反应铁磁材料特性的Uout的关系式［14］:

视实际需要，可依据客户选择，在带有校准孔的仪器设备中，将柔性T型热电偶温度传感器放置于校准孔内，并采用上述同样记录方法测量其温度示值误差，间隙较大时需采用隔热材料堵塞孔口处。[2]

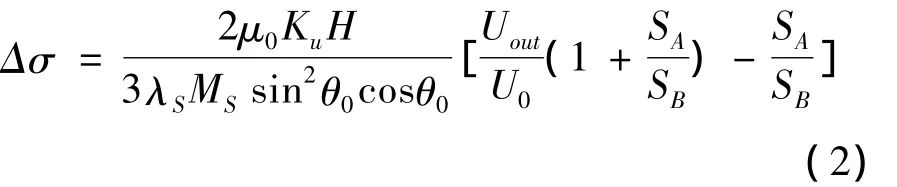
可以看出感应电压积分与应力值之间存在确定的函数关系，通过实验对钢绞线进行标定实验，可以获得相应的标定公式，用于应力监测。

根据此工作原理，我们设计并制作了基于磁弹效应的预应力钢绞线的应力监测系统。系统组成如图2所示。系统包括五个部分:传感器、数据采集卡、磁弹仪(驱动电路)、工业计算机及运行在工业计算机上的软件系统。其中，传感器由励磁线圈、测量线圈以及用于屏蔽磁场和其他信号干扰的保护装置组成;采集装置选用美国国家仪器公司的数据采集模块;磁弹仪是磁通量传感器测试系统的核心设备，主要用于励磁及系统电路控制;工业计算机是作为软件运行、数据处理及信号发送的硬件载体，可以适应工业级别的安全和稳定性要求;软件采用基于LabVIEW图形语言进行编程，高效、稳定，能够长时间进行数据采集和分析。

3 实验装置

实验装置主要包括钢绞线、系统测试软件、采集卡、磁弹仪、传感器样品、工控机和实验加载设备。

实验采用的钢绞线标号为15－7Φ5。规格为单根七股、直径15．5 mm、外包环氧树脂皮层、标准强度为1 860 MPa。

图2 基于磁弹效应的应力监测系统Fig．2 EM effect based stress monitoring system

基于美国国家仪器公司的LabVIEW开发环境开发了一套钢绞线应力监测软件。通过采集与控制模块(NI 6221)对磁弹仪中的电容器进行充放电，实现励磁与测量过程。

磁通量传感器样品为尼龙骨架(绝缘、不导磁)上绕制一定匝数的励磁线圈和测量线圈，外包屏蔽材料防止周围电磁信号及其他干扰源的信号扰动。

实验的加载设备为自制加载架(图3)，采用柳州桥姆YDC-250千斤顶和ZB4－500电动油泵对钢绞线进行加载。钢绞线预先穿过磁通量传感器，并将磁通量传感器固定在钢绞线上，然后将钢绞线两端锚固在加载架上。在其中一端的锚具下安装压力传感器，以获得标定应力信息。

图3 加载装置Fig．3 The loading device

4 测试实验与分析

本文设计并进行了两个实验:第一个实验为对单根钢绞线进行张拉，并用传感器进行测试;第二个实验作为对比实验，在实验一的基础上，将所张拉的钢绞线和磁通量传感器周围放置同样规格的多根钢绞线，以模拟现场环境，验证周围钢绞线即铁磁材料对应力监测系统的测试影响。

4．1 实验一:单根钢绞线应力测试

实验中根据预应力钢绞线的工作范围确定了加卸载区间为50 kN到180 kN。每隔35 kN为一个荷载步，每个荷载步静置1 min，实验中从50 kN加载到180 kN，再按相同荷载步卸载到50 kN，作为一个加卸载循环。单个荷载步加载到位之后的静置时间内，励磁电路及采集设备开始工作，每次励磁到采集结束为一次测量，每个荷载步中重复测量多次，多次测量数据取平均值以减少测量误差。

图4是实验一中对单次荷载测量获得的19次磁特征量(感应电压积分)的散点图，其中纵轴表示感应电压积分值，即磁通量，横轴表示采集次序或者测量序列。由图4可以看出19次测量值都在均值(7．944)附近。通过统计分析得到，标准差为1．29%左右，因而具有很高的测量重复性。

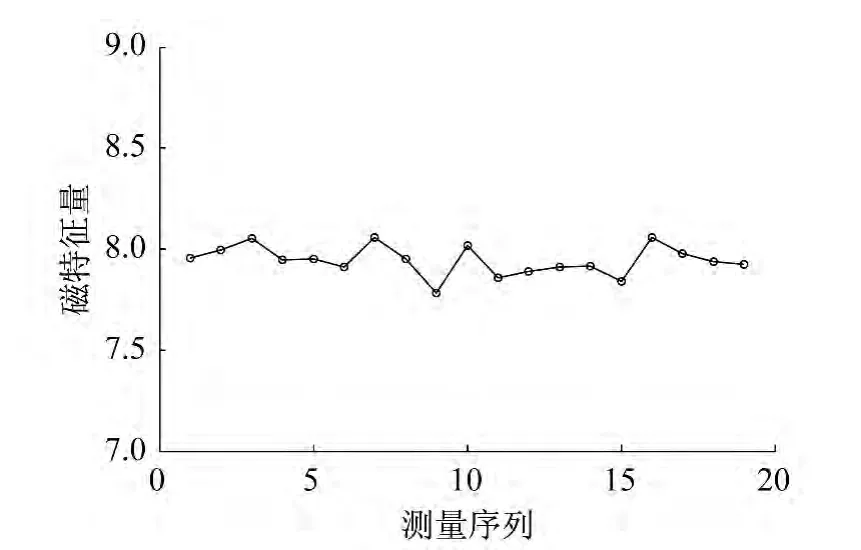
图4 实验一单荷载测试磁特征量分布图Fig．4 Multiple test results for a single load(test 1)

图5 为应力测试系统的标定曲线，图6为拟合值与实验值的对比情况，图7为拟合值与实验值之间相对于满量程(180kN)的百分比误差。

由图5可知:在50 kN～180 kN的测量范围内，对传感器的选定励磁区间内的磁特征量进行线性拟合，拟合结果为 y=410．67 －32．263x，线性相关系数R=0．99874。由此可以看出，磁通量与钢绞线所受到的力之间具有较高的线性度。由图6和图7可知，在考虑到满量程为180 kN的情况下，误差百分比最大在2．25%左右，实验误差值较小，满足工程需要。

4．2 实验二:周围有其他钢绞线的应力测试

在单根钢绞线周围外置若干相同型号的钢绞线束，作为铁磁材料，可以对磁通量传感器的励磁线圈产生的励磁磁场会产生影响。本实验采用了前述未加周围钢绞线工况相同的加载过程，测得拟合结果如图8所示。

图5 实验一力与磁特征量关系Fig．5 Relation between force and magnetic quantity(test 1)

图6 实验一拟合值与实验值对比Fig．6 Comparison between fitting and experimental results(test 1)

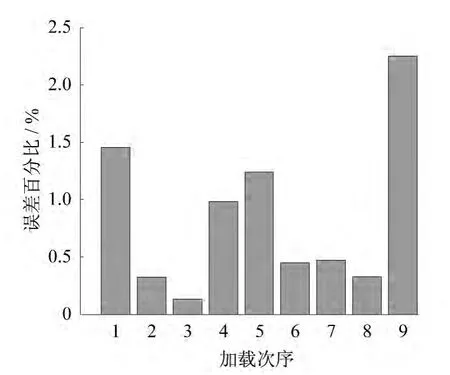
图7 实验一百分比误差Fig．7 The percentage error(test 1)

图8 实验二力与磁特征量的关系Fig．8 Relation between force and magnetic quantity with magnetic disturbance(test 2)

图9 为实验二中拟合值与实验值的对比情况，图10为拟合值与实验值之间相对于满量程(180kN)的百分比误差。

在实验二中，最大误差为3kN以下，误差百分比最大为1．5%左右，实验误差值较小，满足工程需要。

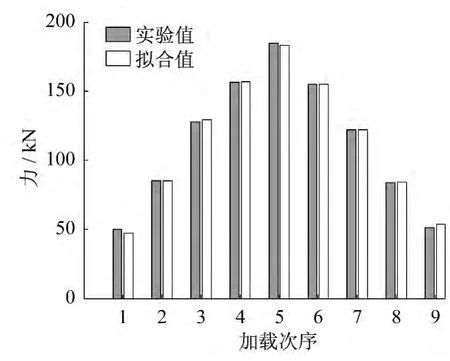
图9 实验二拟合值与实验值对比Fig．9 Comparison between fitting and experimental results(test 2)

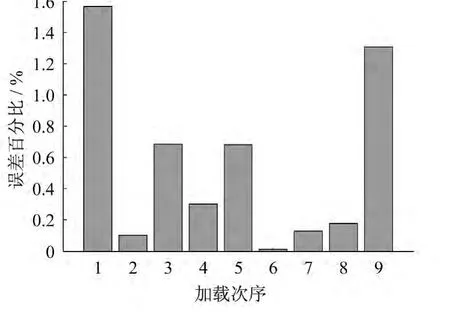
图10 实验二百分比误差Fig．10 The percentage error(test 2)

4．3 实验一与实验二的对比分析

实验一与实验二的区别在于，后者是在被测钢绞线以及测试传感器的周围放置了相同规格的钢绞线，从而为被测钢绞线周围添加了铁磁材料。目的在于验证铁磁材料对传感器的测试结果的影响。

这里将实验二测得的磁特征值带入实验一得到的标定公式中，得出基于实验一的计算值，并与实验二中钢绞线实际的加载值相比较，如图11、12所示。

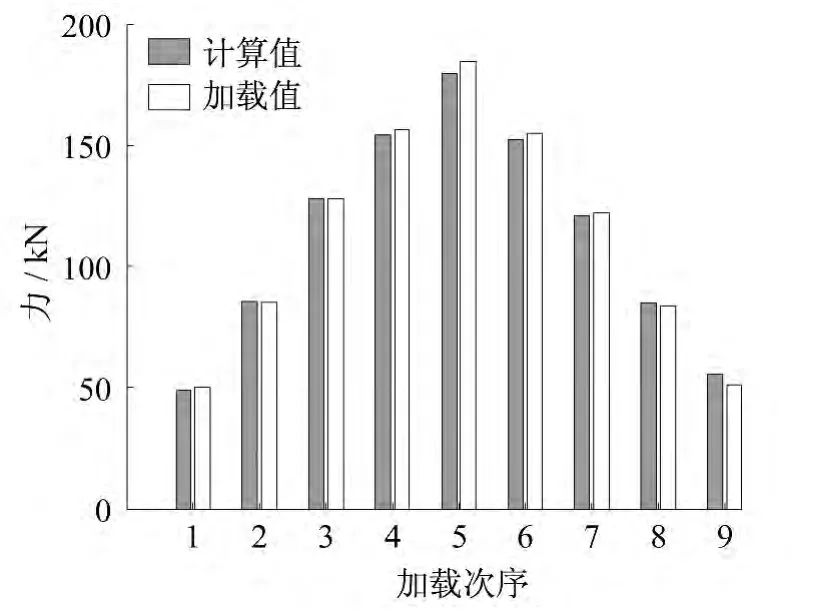
图11 计算值与加载值对比Fig．11 Comparison between calculated value and loading value

图12 计算值与加载值的百分比偏差Fig．12 The percentage relative difference between calculated value and loading value

由图12可以看出，将实验二测得的磁特征量带入到实验一的标定公式，得到的计算值与实验二的加载值最大百分比偏差为满量程的2．5%。注意到用周围无钢绞线的标定公式作为周围有钢绞线的传感器标定公式，其测量的最大百分比偏差(2．5%)与实验一周围无钢绞线应力测试百分比误差(2．25%)相差不大，可以得出周围钢绞线对本传感器的测量影响可忽略的结论。

6 结论

本文介绍了基于磁弹效应的钢绞线全量应力监测系统的工作原理和系统组成，开发了相应的软硬件系统，并对周围有无钢筋两种情况下的单根钢绞线预应力进行测试。得到了以下结论:

(1)基于磁弹效应的应力监测系统，不需要了解受力历史，可直接对钢绞线的应力进行非接触式监测，且具有较高的测试精度(相对误差为2．3%)和良好的重复性(测试标准差为1．3%)。

(2)所研发的应力监测系统，由于采用了合适的磁屏蔽措施，用周围无钢绞线(铁磁材料)的标定公式进行有钢绞线情况下的测试，与实际加载值的相对偏差为2．5%，与传感器自身标定误差(2．3%)相当，因而周围铁磁材料的影响可忽略。

［1］ 叶见曙．结构设计原理［M］．北京:人民交通出版社，2006．Ye Jianshu．Principle of Structural Design［M］．Beijing:China Communications Press，2006．

［2］ 卢伟升，陈常松，涂光亚，等．振弦式应变传感器的温度影响修正［J］．传感器与微系统，2006，(08):49-51转54．Lu Weisheng，Chen Changsong，Tu Guangya，et al．Correction for temperature effect for vibration wire sensor，Transducer and Micro-system Technologies，2006(08):49-51 and 54．

［3］ 梁磊，王艳妮，刘德力．粘贴式光纤光栅应变传感器的应变传递分析［J］．武汉理工大学学报，2008，(10):144-146．Liang Lei，Wang Yanni，Liu Deli．Strain transferring analysis of pasted strain fiber Bragg grating sensor．Journal of Wuhan University of Technology，2008(10):144-146．

［4］ 金秀梅，彭彦彬，杜彦良．大型预应力混凝土结构预应力筋应力测试技术研究［J］．铁道建筑，2008(9):15-17．Jin Xiumei，Peng Yanbin，Du Yanliang．Prestress testing technology for prestressed Tendons of largescale prestressed concrete structures．Railway Engineering，2008(9):15-17．

［5］ 殷莉娜，缪峰，李威．索力测试频率法的研究［J］．山西建筑，2007，33(32):335-336．Yin Lina，Miao Feng，Li Wei，The research of frequency method of cable force measurement［J］．Shanxi Architecture，2007，33(32):335-336．

［6］ 王修勇，谭艳．斜拉桥拉索减振阻尼器对拉索索力测量的影响研究［J］．振动与冲击，2008，28(11):80-82．Wang Xiuyong，Tan Yan．Study of cable tension measurement for stay cable attached with dampers．Journal of Vibration and Shock，2008，27(11):80-82．

［7］ Chaki S，Bourse G．Guided ultrasonic waves for nondestructive monitoring of the stress levels in prestressed steel strands．Ultrasonics，2009，49(2):162-171．

［8］ Wang M L，Chen Z L，Koontz S S，et al．Magnetoelastic permeability measurement for stress monitoring in steel tendons and cables［J］．Nondestructive Evaluation of Highways，Utilities，and Pipelines IV，A．Emin Aktan，Stephen R．Gosselin，Editors，Proceedings of SPIE，2000，Vol．3995:492-500．

［9］ Joh C，Lee J W，Kwahk I．Feasibility study of stress measurement in prestressing tendons using Villari effect and induced magnetic field［J］．International Journal ofDistributed SensorNetworks，Volume 2013，Article ID 249829，8 pages．

［10］ 缪长青，韩惠婷，李爱群，等．江阴大桥原结构安全监测系统设计分析［J］．公路交通科技，2007，24(11):81-86．Miao Changqing，Han Huiting，LI Aiqun，et al．A-nalysis on the Original SHM System of Jiangyin Bridge，Journal of Highway and Transportation Research and Development，2007，24(11):81-86．

［11］ 黄腾，郑玉华，武焕陵，等．南京长江第二大桥结构安全监测系统［J］．河海大学学报 (自然科学版)，2003，31(4):411-414．Huang Teng，Zheng Yuhua，Wu Huanling，et al．Structural safety monitoring system for the Second Nanjing Yangtze River Bridge．Journal of Hohai University(Natural Sciences)，2003，31(4):411-414．

［12］ 龙跃，邓年春，朱万旭．磁通量传感器及其在桥梁监测中的应用［J］．预应力技术，2007(2):3-6．Long Yao，Deng Nianchun，Zhu Wanxu．Magnetic flux sensor and its application to bridge monitoring．Prestress Technology，2007(2):3-6．

［13］ 文西芹，张永忠，宁晓明．逆磁致伸缩效应扭矩传感器的历史、现状、趋势［J］．传感器世界，2002(2):1-7．Wen Xiqin，Zhang Rongzhong，Ning Xiaoming．The History，Actuality and Trend of Torque Sensors based on Magnetostrictive Effect［J］．Sensor World，2002(2):1-7．

［14］ 尹文霞，周仙通，段元锋，等．基于磁弹效应的高强钢丝应力监测实验研究［J］．结构工程师，2013，29(5):113-118．Yin Wenxia，Zhou Xiantong，Duan Yuanfeng，et al．Elasto-magnetic effect based stress monitoring of highstrength steel wires:experimental investigation．