油松林分断面积生长预估模型研究

高东启 邓华锋 蒋 益 程志楚

(1.北京林业大学林学院，北京 100083；2.国家林业局调查规划设计院，北京 100714)



油松林分断面积生长预估模型研究

高东启1邓华锋1蒋 益1程志楚2

(1.北京林业大学林学院，北京 100083；2.国家林业局调查规划设计院，北京 100714)

在森林经营中，间伐林分、未间伐林分分开单独建模存在不相容的问题，有必要对其进行研究，并建立统一的模型。利用森林资源一类清查数据，以Schumacher模型为基础，通过引入哑变量、间伐指标分别建立北京市油松林分断面积生长预估模型，使得间伐林分和未间伐林分能够整合在一起建立统一的模型。经检验，引入哑变量模型对油松林分断面积的预测精度最低，为87.99%；其次是引入间伐指标模型，预估精度为88.36%；综合引入哑变量和间伐指标模型预估精度最高，为88.61%。所建模型对间伐林分和未间伐林分均适用，更方便于在实践中应用。

林分断面积；哑变量；间伐指标；油松

油松(Pinustabulaeformis)是北京市主要的绿化树种，多为人工林，天然林较少，在保护首都生态环境安全方面发挥着重要作用。据第七次全国森林资源清查统计[1]，油松占北京市森林面积总量的18.7%，占蓄积总量的11.9%。为了提高林分的质量和效益、科学合理的经营管理森林资源，有必要通过生长模拟来掌握林分的生长状况。现实林分由于受间伐措施的影响，使得间伐林分的生长规律、空间结构和生态环境相对未间伐林分都可能发生变化[2-4]。从理论上讲，同一树种的间伐林分与未间伐林分需要分开单独建立模型，而间伐林分与未间伐林分之间是存在一定联系的，因此如何将这两种类型的林分整合在一起建立统一的模型是当前急需解决的问题，同时也使得间伐林分与未间伐林分生长模型能够紧密联系形成一个有机的整体。关于间伐林分的研究，国外的Bailey等[5]在建立林分断面积生长预估模型时加入了一个表示间伐的自变量，Murray等[6]考虑用分布函数来表示间伐对林分断面积生长的影响，Pienaar等[7]提出了由未间伐林分预估间伐林分的新思路；国内的杜纪山、李春明等研究了间伐对杉木(Cunninghamialarceolata)、落叶松(Larixgmelini)人工林生长的影响[8-10]。

本研究以油松人工林为例，从相容的角度出发，以Schumacher模型为基础，分别引入哑变量[11-12]、间伐指标[7]，建立间伐林分和未间伐林分相容的、统一的油松林分断面积生长预估模型，并对模型的预测能力进行分析比较。

1 研究区概况

北京市位于北纬39°28′～41°05′，东经115°25′～117°30′，地处华北平原北端，北以燕山山地与内蒙古高原接壤，西以太行山与河北省相连，东北与松辽平原相通，南与黄淮海平原连片；属于暖温带半湿润大陆性季风型气候，四季分明，夏季炎热多雨，冬季寒冷干燥，夏季降水量占全年降水量的74%。

2 研究方法

2.1 样地调查及数据整理

本研究所采用的数据为北京市一类清查数据，每个样地的面积为 0.066 7 hm2。样地调查因子有：林木胸径、林分年龄、林分平均高、林分蓄积、采伐蓄积等。所使用的数据分别调查于1996、2001、2006年，3期数据共计组成99个样本，其中，间伐林分56个，未间伐林分43个，部分样地在调查间隔期内进行了间伐，间伐强度不固定，间伐间隔期5 a。间伐林分与未间伐林分样地的基本情况见表1。主要统计了林分的平均年龄、平均胸径、平均树高、单位面积株数、单位面积断面积和单位面积蓄积量。

表1 间伐林分和未间伐林分主要因子统计

从表1中可以看出，油松间伐林分的平均年龄、平均胸径、平均树高、单位面积断面积和单位面积蓄积量要明显大于未间伐林分，而单位面积株数又小于未间伐林分，说明间伐效果明显。

对99个样本进行随机抽样，其中50个样本用于建模，包含间伐林分31个、未间伐林分19个；49个样本用于检验，包含间伐林分25个、未间伐林分24个，样地分布情况见表2。

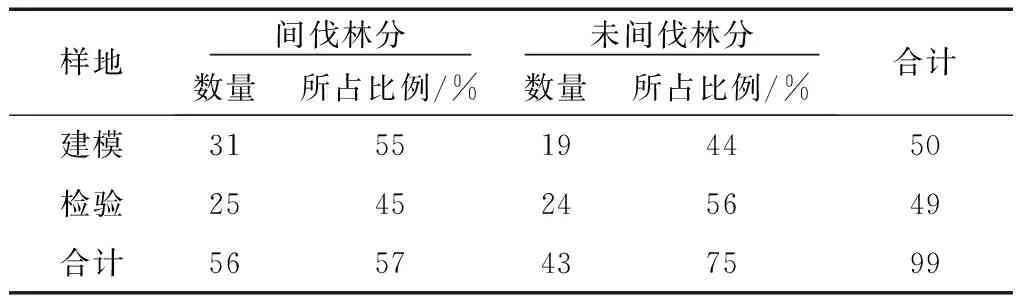
表2 随机抽样样地分布情况

2.2 林分优势木平均高计算

林分优势木平均高与林分平均高呈线性关系，由于所用资料中没有油松林分优势木平均高的相关记录，参考贺姗姗[13]的研究结果，其通过解析优势木的方法，得到油松人工林优势木平均高与林分平均高的相关关系：

H=1.115h+0.429 3

(1)

式中：H为林分优势木平均高；h为林分平均树高；相关系数为0.952 1。

通过(1)式计算出各样地的林分优势木平均高，作为评价林分立地质量的指标。

2.3 基于哑变量的方法

通过引入哑变量[11]将油松间伐林分和未间伐林分2个类型的林分用定性代码来表示，具体过程是将第i个类型的林分编号为Ki，将定性数据Ki转化为(0,1)：

式中：i=1,2；K1、K2分别为间伐林分和未间伐林分的定性代码。

为了和下面的方法进行对比，选用Schumacher模型建立林分断面积生长预估模型，其基本形式为[7]：

G=exp(a1+a2/t)Na3+a5/tHa4+a6/t

(2)

为了减小建模时所产生的异方差，可采用对数回归的方法[14]，对Schumacher模型两边取对数变为如下形式：

lnG=a1+a2/t+a3ln(N)a4ln(H)+a5ln(N)/t+a6ln(H)/t

(3)

参考李忠国等建立哑变量模型的方法[12]，将哑变量引入到模型(3)式的参数中。经过初步尝试，发现在参数a0～a6中分别引入哑变量时模型的决定系数是不同的。其中，在a4中引入哑变量时模型的决定系数最高，说明表示油松间伐、未间伐林分的哑变量对参数a4的影响最大，既将哑变量引入到模型(3)式的a4中最为合理，则确定哑变量模型的最终形式如下：

lnG=a1+a2/t+a3ln(N)+(a4K1+a5K2) ln(H)+a6ln(N)/t+a7ln(H)/t

(4)

式(2)、(3)、(4)中：G为单位面积林分断面积；lnG为林分断面积的对数形式；H为林分优势木平均高；N为林分单位面积株数；t为林分平均年龄；a1～a7为待定参数；K1、K2分别为间伐林分和未间伐林分的定性代码。

采用含有哑变量的模型(4)式建立油松间伐林分和未间伐林分相容的林分断面积生长预估模型，并估计各个参数值。

2.4 引入间伐指标的方法

有学者研究发现[7]，间伐林分与未间伐林分断面积差异的大小取决于间伐时的年龄和间伐强度，并且得到间伐林分和未间伐林分相容的断面积预估方程：

lnG=a1+a2/t+a3ln(N)+a4ln(N)+a5ln(H)/t+a6ln(H)/t+a7Nftf/(Nat)

(5)

式中：G为单位面积林分断面积；lnG为断面积的对数形式；N为林分单位面积株数；H为林分优势木平均高；t为林分现在的平均年龄；Nf为最近一次间伐中伐去林木株数；tf为林分最近一次间伐时的年龄；Na为最近一次间伐后保留林木株数；a1～a7为待定参数。

模型(5)式相对于对数形式的Schumacher模型(3)式而言，实际上是在(3)式的基础上引入了一些表示间伐林分特征的相关指标，有表示间伐强度的Nf和Na，还有表示间伐年龄的tf。直接用(5)式去预估林分的断面积，由于引入了间伐指标，也使得间伐林分与未间伐林分在建模时具有相容性。

2.5 综合引入哑变量和间伐指标的方法

在上述引入哑变量或间伐指标的2种方法的基础上，在Schumacher模型(3)式中同时引入哑变量和间伐指标，作为预估间伐林分与未间伐林分断面积的第3种方法，其形式如下：

lnG=a1+a2/t+a3ln(N)+(a4K1+a5K2)ln(H)+a6ln(N)/t+a7ln(H)/t+a8Nftf/(Nat)

(6)

式中：G为单位面积林分断面积；lnG为林分断面积的对数形式；N为林分单位面积株数；H为林分优势木平均高；t为林分现在的平均年龄；Nf为最近一次间伐中伐去林木株数；tf为林分最近一次间伐时的年龄；Na为最近一次间伐后保留林木株数；a1～a8为待定参数；K1、K2分别为间伐林分和未间伐林分的定性代码。

2.6 参数估计与模型检验

综合应用ForStat、Excel、SPSS进行数据处理和参数估计，计算均方根误差(RMSE)、总相对误差(TRE)、平均系统误差(MSE)、预估精度(P)等指标来检验模型的预测能力，同时对所建模型进行成对t检验。

3 结果与分析

统计各模型的参数估计结果见表3。哑变量模型(4)式的拟合效果最差，决定系数R2为 0.845 0；其次是引入间伐指标的模型(5)式，决定系数R2为 0.846 2；综合引入了哑变量和间伐指标的模型(6)式拟合效果最好，决定系数R2为 0.846 9，平均绝对偏差(MAD)和均方根误差(RMSE)最小。

表3 模型参数统计

利用检验数据对模型(4)、(5)、(6)式进行检验，统计结果见表4。在表4中，哑变量模型(4)式的各项误差最大，预估精度最低，为87.99%；引入间伐指标的模型(5)式居中，预估精度为88.36%；综合引入哑变量和间伐指标的模型(6)式预估精度最高为88.61%，各项误差均较小。进行成对t检验，结果为Sig.<0.05，说明在0.05显著水平上模型的回归效果显著，实测值与预测值无显著差异，所建的林分断面积模型比较合理。

进一步检验模型对间伐林分、未间伐林分断面积的预测能力，统计结果见表5。从表5中可以看出：对于间伐林分而言，模型(4)、(5)、(6)式的预测精度分别为91.86%、91.90%、91.96%，预测效果较好，预测误差以(4)式最大，(6)式最小；对于未间伐林分而言，模型(4)、(5)、(6)式的预测精度分别为83.17%、84.47%、85.23%，以(6)式误差最小，这说明综合引入哑变量和间伐指标的模型(6)式要优于模型(4)、(5)式，而引入间伐指标的模型(5)式对间伐、未间伐林分的预测效果又要好于引入哑变量的模型(4)式。

表4 模型检验

表5 模型对间伐、未间伐林分的预测效果检验

4 结论与讨论

以Schumacher模型为基础，采用3种方法将间伐林分与未间伐林分整合在一起分别建立北京市油松人工林的断面积生长预估模型，经检验，模型对油松林分断面积的预估效果都较好，预估精度在87%以上。无论是引入哑变量或间伐指标，还是综合引入哑变量和间伐指标，都能使得间伐林分和未间伐林分整合在一起建立统一的模型，从而使2种不同类型的林分生长模型形成一个有机联系的整体，既适用于间伐林分，也适用于未间伐林分，便于在实践中应用。

3种方法由于引入的因子不同，其预估效果也不相同。引入哑变量的模型对油松林分断面积的预测精度最低，为87.99%；其次是引入间伐指标的模型，预估精度为88.36%；综合引入哑变量和间伐指标的模型预估精度最高，为88.61%。可能的原因是引入间伐指标增加了林分状况的有效信息，使模型的预测效果更好；而引入哑变量并不能增加林分信息因子，只是调整了模型结构建立了间伐林分和未间伐林分相统一的模型；综合引入哑变量和间伐指标不仅提高了模型对林分信息的利用程度，同时还优化了模型结构，使其预测效果最好。

由于本研究所用数据有限，且时间间隔较短，下一步对于油松间伐林分的研究可进一步收据信息更加丰富、内容更加全面的长期观测数据，考虑区域效应、样地效应、时间效应等随机因素和其他经营管理措施对模拟林分生长的影响。

[1] 贾忠奎，马履一，徐程扬，等．北京市森林资源动态及可持续经营对策[J]．干旱区资源与环境，2006，20(3)：30-36．

[2] 李春明，杜纪山，张会儒．抚育间伐对森林生长的影响及其模型研究[J]．林业科学研究，2003，16(5)：636-641．

[3] 杜纪山，唐守正．抚育间伐对林分生长的效应及其模型研究[J]．北京林业大学学报，1996，16(1)：80-84．

[4] 岳永杰，余新晓，李钢铁，等．北京松山自然保护区蒙古栎林的空间结构特征[J]．应用生态学报，2009，20(8)：1811-1816．

[5] Bailey R L, Ware K D. Compatible basal area growth and yield model for thinned and unthinned stands[J]. Canadian Journal Forest Research, 1983(13): 563-571.

[6] Murray D M, Von G K. Relationships between the diameter distributions before and after thinning[J]. Forest Science, 1991, 37(2): 552-559.

[7] Pienaar L V, Shiver B D. Basal area prediction and projection equations for pine plantations[J]. Forest Science, 1986, 32(3): 626-633.

[8] 杜纪山，唐守正．杉木林分断面积生长预估模型及其应用[J]．北京林业大学学报，1998，20(4)：4-8．

[9] 李春明，杜纪山，张会儒．间伐林分的断面积生长模型研究[J]．林业资源管理，2004(3)：52-55．

[10] 李春明，杜纪山，张会儒．抚育间伐对人工落叶松断面积和蓄积生长的影响[J]．林业资源管理，2007(3)：90-93．

[11] 唐守正，郎奎建，李海奎．统计与生物数学模型计算(ForStat教程) [M]．北京：科学出版社，2009．

[12] 李忠国，孙晓梅，陈东升，等．基于哑变量的日本落叶松生长模型研究[J]．西北农林科技大学学报:自然科学版，2011，39(8)：69-74．

[13] 贺姗姗．北京山区油松人工林林分结构与生长模拟研究[D]．北京：北京林业大学，2009．

[14] 曾伟生，唐守正．非线性模型对数回归的偏差校正及与加权回归的对比分析[J]．林业科学研究，2011，24(2)：137-143．

(责任编辑 赵粉侠)

Forecast Models Research of Stands Basal Area Growth forPinustabulaeformis

GAO Dong-qi1,DENG Hua-feng1,JIANG Yi1,CHENG Zhi-chu2

(1.College of Forestry, Beijing Forestry University, Beijing 100083, China; 2.Academy of Forest Inventory and Planning, State Forestry Administration, Beijing 100714, China)

It was incompatible to model thinned stands and unthinned stands separately, so it was necessary to study and establish the unified models. Using forest inventory data, based on Schumacher model, through introducing the dummy variables and thinning indexes to establish the stands basal area growth forecast models ofPinustabulaeformisin Beijing respectively, and made the thinned stands and unthinned stands together to establish unified models.After inspection,on the forecast effect for stands basal area ofPinustabulaeformis, forecast accuracy of model with dummy variables was 87.99% as a minimum; followed by the model with thinning indexes, forecast accuracy was 88.36%;forecast effect of model with dummy variables and thinning indexes was the best, forecast accuracy was as high as 88.61%.The models was applicable for thinned stands and unthinned stands, it was more convenient for application in practice.

stands basal area;dummy variables;thinning indexes;Pinustabulaeformis

2014-04-29

林业公益性行业科研专项(201204510)资助。

邓华锋(1966—)，男，博士，教授。研究方向：森林可持续经营。Email：denghuafeng@bjfu.edu.cn。

10.11929/j.issn.2095-1914.2015.01.009

S758.5

A

2095-1914(2015)01-0042-05

第1作者：高东启(1986—)，男，硕士生。研究方向：森林可持续经营。Email:511602746@qq.com。