基于Matlab的概率积分法开采沉陷预计参数解算

沈 震 徐良骥 刘 哲 秦长才

(安徽理工大学测绘学院，安徽 淮南 232000)

基于Matlab的概率积分法开采沉陷预计参数解算

沈 震 徐良骥 刘 哲 秦长才

(安徽理工大学测绘学院，安徽 淮南 232000)

通过在开采工作面地表建立观测站获取地表变形数据解算概率积分法开采沉陷预计参数，从而预计工作面周边或相似开采条件下工作面的开采沉陷并评估和指导开采作业，其前提是精确获取概率积分法开采沉陷预计参数。为此，基于Matlab软件，采用最小二乘法拟合观测点变形数据解算概率积分法开采沉陷预计参数，并结合Matlab软件绘图工具开发了集数据载入、坐标转换、参数解算、结果输出、开采沉陷预计及反演为一体的可视化开采沉陷预计系统。以淮南谢桥煤矿11316工作面为例，根据地表移动观测点位移数据解算开采沉陷预计参数并与实测值进行对比分析，结果表明，该系统解算出的开采沉陷预计参数符合两淮矿区开采沉陷的基本规律，反演结果与实测值基本吻合，该系统对于实现矿区开采沉陷高精度预计和反演具有一定的参考价值。

开采沉陷 概率积分法 开采沉陷预计系统 最小二乘法 Matlab

开采沉陷会改变矿区原始地表状态，对矿区环境及周边居民生产生活造成影响，因此有必要对开采沉陷进行精确预计以便有计划地进行开采作业[1-3]。开采沉陷的预计方法有概率积分法、负指数函数法，典型曲线法等，其中概率积分法应用较广泛[4-6]。本研究借助Matlab软件丰富的内置函数与强大的数据处理功能，实现根据任意点变形量解算概率积分法开采沉陷预计参数，并结合该软件的绘图工具开发出可视化开采沉陷预计系统。

1 系统主要功能

1.1 概率积分法模型

以自定义函数的形式建立概率积分法模型，并保存在单独的M文件中，该模型程序代码如下：

Function Wz= probability_integration_method (data2，xy)

l=data1 (1)-data2 (3)-data2 (4);

L=data1 (2)-data2 (5)-data2 (6))*sin (data2 (7) +data1 (3))/sin (data2 (7));

CX=1/2*(erf(pi^(1/2)*xy(:,1)*data2(2)/data1(4))-erf(pi^(1/2)*(xy(:,1)-l)*data2(2)/data1(4)));

CY=1/2*(erf(pi^(1/2)*xy(:,2)*data2(2)/data1(5))-erf(pi^(1/2)*(xy(:,2)-L)*data2(2)/data1(6)))

Wmax=data1 (7)*data2 (1)*cos (data1 (3));

WZ=Wmax*CX.*CY.

(1)已知参数。包括L0、L1、a、H0、H1、H2和M。L0、L1分别为走向和倾向线长度，m；a为煤层倾角，(°)；H0为平均开采深度，m；H1、H2分别为下山及上山方向开采深度，m；M为煤层开采厚度，m。已知参数以向量的形式保存于“data1”中，调用时按顺序记为data1(n)。

(2)预计参数。包括q、tanβ、S1、S2、S3、S4和θ0。q为下沉系数；tanβ为主要影响角正切值；S1、S2为走向线两端拐点偏距，m；S3、S4为倾向线下山和上山方向拐点偏距，m；θ0为影响传播角，(°)[7]。待求参数以向量形式保存于“data2”中。

(3)点坐标。地表观测点在工作面坐标系中的坐标为(x,y)。

1.2 数据载入和坐标转换

将所有观测点的坐标值、下沉量和水平移动量按一定格式保存于Excel或.txt文档中，通过“xlsread”、“textread”等命令读取数据。Matlab软件可将所有数据保存在一个矩阵中，按需要从该矩阵中提取坐标值、下沉量和平移量等信息，并保存在相应的数据矩阵中，便于调用[8]。

概率积分法通常采用独立坐标系(工作面坐标系)预计开采沉陷。开采工作面多为矩形，以工作面的西南端点为原点，X轴沿工作面走向线方向，Y轴沿工作面倾向线方向并与X轴垂直，建立工作面坐标系，见图1。图1中，矩形ABCD为开采工作面，XOY为测量坐标系，X′O′Y′为工作面坐标系[9-10]。

图1 工作面坐标系

坐标转换时将点D在XOY坐标系中的坐标作为平移参数，在CAD软件中量取工作面的倾斜角度作为旋转参数(如无特殊要求可不考虑尺度参数)。当工作面范围较大时，也可根据2个或2个以上公共点在2套坐标系中的坐标，采用最小二乘法求解坐标转换参数，坐标转换模型为[11-12]

(1)

式中，(x′,y′)、(x,y)分别为点E在XOY测量坐标系和X′O′Y′工作面坐标系中的坐标；α为旋转角度，(°)；x0、y0为平移参数，m。

将获取的坐标转换参数以向量形式保存于“p1”中，定义坐标转换函数，程序代码如下：

Function x1=coordinate_transformation (p1,X0)

for k=1:length(X0);

X1(k，:) = (X0(k，:)-[p1 (1)，p1 (2)]) ;

X1(k，:) = [cos (p1 (3))，sin (p1 (3));-sin (p1 (3))，cos (p1 (3))]*X1(k，:)′.

end

调用函数“coordinate_transformation”可完成由测量坐标系至工作面坐标系的转换。

1.3 解算概率积分法预计参数

监测点在工作面坐标系中的坐标为(x,y)，实际下沉量为z，采用最小二乘法进行曲面拟合，经过多次迭代求取1组参数，使得拟合曲面与实测结果偏差的平方和最小，数学模型为[13-14]

(2)

式中，V1为各监测点实测下沉量与最小二乘拟合值的偏差，m；V2为各监测点实测水平变形量与最小二乘拟合值的偏差，m;k为监测点数目；Wzk、Uk分别为各监测点实测下沉和水平变形量，m；W(x,y),U(x,y)分别为各监测点实测下沉和水平变形量的最小二乘拟合值，m，可调用Matlab软件中的“lsqcurvefit”函数[15]进行拟合得到。程序代码如下:

X1=coordinate_transformation (p1，X0);

ff=optimset; ff.MaxFunEvals=2^12; ff.TolFun=1e-10; ff.TolX=1e-10;

[data2,resnorm，residual]=lsqcurvefit (@probability_integration_method，data0，X1，Wz).

程序中，“X1”、“Wz”为监测点在工作面坐标系下的坐标和对应的下沉量；“data0”为参数迭代初始值包含了7个变量，其格式与“data2”一致，初值的选取直接影响预计参数的解算精度，可参考开采工作面地质及技术资料确定[16]。函数返回值包括预计参数的拟合最佳值(data2)、监测点拟合残差(residual)、监测点拟合残差的平方和(resnorm)，将解算所得参数作为已知值，根据水平移动量可解算监测点水平移动参数。

1.4 开采沉陷反演及预计

解算出开采沉陷预计参数后，将已知参数和预计参数代入概率积分法模型计算开采沉陷区域内的地表变形量，并采用Matlab软件中的“ezmesh”、“ezcontour”函数绘制下沉曲面及下沉等值线图，从而预计或反演地表变形结果，程序代码如下[17-21]:

syms x; syms y;

xy=[x,y]

ezmesh (coordinate_transformation(data2,x,y),[min_x,max_x],[ min_y,max_y]);

ezcontour (coordinate_transformation(data2,x,y)，[min_x,max_x],[ min_y,max_y]);

程序中，“min_x”、“max_y”分别为X、Y轴上的绘图边界，绘图结果见图2、图3。

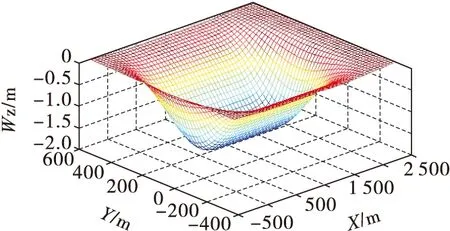
图2 预计下沉曲面

2 应用实例

2.1 开采沉陷预计参数解算

以淮南矿区谢桥矿11316工作面为例，工作面走向长1 980 m，倾向长240 m，煤层倾角15°，平均采深718.3 m，煤层开采厚度3.9 m。地表移动观测站共设置2条观测线，计87个测点，选取其中30个有较高精度并能反映工作面地表变形特点的监测点实测数据作为解算数据，见表1。根据矿区预计参数经验值，取迭代初始值data0=[0.7;2;25;25;10;5; 1.31]进行最小二乘拟合，可得q=0.798，tanβ= 1.755，S1=35.97，S2=35.47，S3=9.996、S4=4.996，θ0=1.133。

图3 地表下沉等值线

表1 11316工作面部分观测点实测数据

Table1 Part of measured date at observation points of 11316 working face m

点 号XY下沉量ml01-14.41130.850.793ml0217.00139.570.885ml0347.85135.891.010ml0476.58136.241.131ml08225.37132.861.642ml10346.98135.541.670ml11377.39128.581.661ml17555.05126.511.457ml18585.66128.761.695ml21675.94120.781.717ml23826.03137.071.637ml24856.07134.051.661ml291215.86136.741.689ml301245.91139.921.702ml311275.38133.611.716ml331335.98137.941.638ml351396.63123.481.923ml371456.57138.791.668ml401577.31133.361.613ml411606.03126.611.648ml461876.96122.240.984ml471906.16131.590.817ml491965.44134.130.619ms03939.2621.011.519ms04944.1843.191.445ms07947.51102.591.614ms10950.25162.651.550ms11938.92183.511.583ms13954.14221.461.501ms14941.84242.971.411

2.2 预计参数验证及地表移动变形规律反演

将开采沉陷预计参数代入概率积分法模型计算上述30个监测点的地表变形量的最小二乘拟合值，并与实测数据进行对比，计算拟合残差，结果见表2。

表2 观测点拟合残差

Table.2 Fitting residual of observation points m

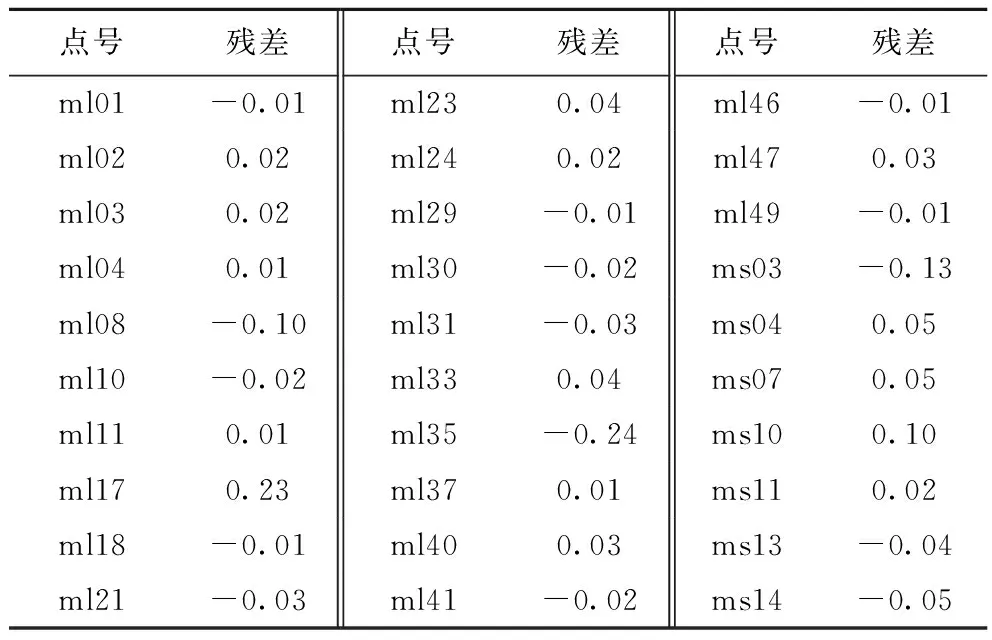
点号残差点号残差点号残差ml01-0.01ml230.04ml46-0.01ml020.02ml240.02ml470.03ml030.02ml29-0.01ml49-0.01ml040.01ml30-0.02ms03-0.13ml08-0.10ml31-0.03ms040.05ml10-0.02ml330.04ms070.05ml110.01ml35-0.24ms100.10ml170.23ml370.01ms110.02ml18-0.01ml400.03ms13-0.04ml21-0.03ml41-0.02ms14-0.05

根据拟合值和拟合残差计算拟合决定系数，公式为

(3)

式中，SSR为拟合值平方和，m2；SSE为残差平方和，m2。

将相关数值代入式(3)，计算得R2=0.997 5，拟合程度较好，拟合值与实测值(表1)较为接近。

采用概率积分法对11316工作面开采沉陷进行反演，并将反演结果与实测值进行对比，结果见表3。

表3 概率积分法反演结果与实测值比较

由表3可知，由反演得到的最大下沉值与实测值的误差仅为0.242 m，其余变形参数反演值和实测值也较为接近。对原始观测数据进行分析可知，达到充分下沉的下沉盆地内监测点实测下沉量为1.60～1.72 m，最大下沉值(1.923 m)对应的是ml35点，为异常点。据此可认为，本研究开发的开采沉陷预计系统能够满足矿区地表沉陷预计的精度要求。

3 结 语

基于Matlab软件，开发了开采沉陷预计系统，该系统采用最小二乘法拟合观测点变形数据解算概率积分法开采沉陷预计参数。淮南谢桥煤矿11316工作面试验结果表明，该系统对于矿区地表沉陷的预计精度较高。

[1] 何国清，杨 伦，凌赓娣，等.矿山开采沉陷学[M].徐州：中国矿业大学出版社，1995. He Guoqing，Yang Lun，Ling Gengdi，et al.Mining Subsidence in Mine [M].Xuzhou:China University of Mining and Technology Press，1995.

[2] 方 齐，郭广礼，朱晓峻.矿区地表观测站辅助设计与数据处理程序实现[J].金属矿山，2015(5)：129-134. Fang Qi，Guo Guangli，Zhu Xiaojun.Realization of aided design of surface movement observation station and data processing in mining area[J].Metal Mine，2015(5)：129-134.

[3] 杨俊凯，范洪冬，赵伟颖，等.基于D-InSAR技术和灰色Verhulst模型的矿区沉降监测与预计[J].金属矿山，2015(3)：143-147. Yang Junkai,Fan Hongdong,Zhao Weiying,et al.Monitoring and prediction of mining subsidence based on D-InSAR and gray verhulst model[J].Metal Mine，2015(3)：143-147.

[4] 姚 琦，冯 涛，李石林，等.基于概率积分法的煤矿“三下”开采沉陷预计[J].煤矿安全，2012(7)：188-190. Yao Qi，Feng Tao，Li Shilin，et al.Subsidence prediction of coal mine “three under” mining based on probability integral method [J].Safety in Coal Mines，2012(7):188-190.

[5] 朱晓峻，郭广礼，方 齐.概率积分法预计参数反演方法研究进展[J].金属矿山，2015(4)：173-177. Zhu Xiaojun，Guo Guangli，Fang Qi.Recent progress on parameter inversion of probability integral method [J].Metal Mine，2015(4):173-177.

[6] 杨俊凯，陈炳乾，邓喀中，等.基于D-InSAR与概率积分法的开采沉陷监测与预计[J].金属矿山，2015(4)：195-200. Yang Junkai，Chen Bingqian，Deng Kazhong，et al.Monitoring and prediction of mining subsidence based on D-InSAR and probability integral method [J].Metal Mine，2015(4):195-200.

[7] 王永辉，倪岳晖，周建伟，等.基于概率积分法的横河煤矿巨厚松散层下开采沉陷预测分析[J].地质科技情报，2014(4)：219-224. Wang Yonghui，Ni Yuehui，Zhou Jianwei.et al.Subsidence prediction under thick and loose overburden of Henghe coal mine based on probability integral method [J].Geological Science and Technology Information，2014(4):219-224.

[8] 刘保柱.MATLAB 7.0从入门到精通[M].北京：人民邮电出版社，2006. Liu Baozhu.MATLAB 7.0 From Beginning to Master [M].Beijing:Post & Telecom Press，2006.

[9] 韩买侠，陈传录，王夏莉.基于Matlab的坐标转换方法研究[J].测绘与空间地理信息，2013(9)：89-91. Han Maixia，Chen Chuanlu，Wang Xiali.Research of coordinate transformation methods based on Matlab [J].Geomatics & Spatial Information Technology，2013(9):89-91.

[10] 汪桂生.矿区开采沉陷观测数据处理研究[D].西安：西安科技大学，2011. Wang Guisheng.Observation Data Processing of Mining Subsidence[D].Xi′an:Xi′an University of Science and Technology，2011.

[11] 梁月吉，谢劭峰，庞光锋.基于Matlab的坐标转换程序设计[J].地理空间信息，2014(2)：124-125. Liang Yueji，Xie Shaofeng，Pang Guangfeng.Design of coordinate transform program design based on Matlab[J].Geospatial Information，2014(2):124-125.

[12] 刘学军.工程测量中平面坐标转换及其应用[J].北京测绘，2014(6)：142-145. Liu Xuejun.Planar coordinate conversion and application in engineering surveying [J].Beijing Surveying and Mapping，2014(6):142-145.

[13] 许 冬，王临清，吴 侃.任意形状工作面沉陷预计计算方法[J].金属矿山，2014(5)：55-59. Xu Dong，Wang Linqing，Wu Kan.Mining subsidence prediction calculation method of random shape working face [J].Metal Mine，2014(5):55-59.

[14] 王 友，王双亭.抗差岭估计在概率积分法预计参数求取中的应用研究[J].煤矿开采，2014(3)：17-19. Wang You，Wang Shuangting.Application of anti-poor-estimation in prediction parameters solution by probability integral method [J].Coal Mining Technology，2014(3):17-19.

[15] 谭衍涛，张兴福.MATLAB拟合工具箱在GNSS高程转换中的应用[J].工程勘察，2014(9)：65-68. Tan Yantao，Zhang Xingfu.Application of MATLAB surface fitting tool for GNSS height transformation [J].Geotechnical Investigation & Surveying，2014(9):65-68.

[16] 邹友峰.开采沉陷预计参数的确定方法[J].焦作工学院学报：自然科学版，2001，20(4)：253-257. Zou Youfeng.Determining method of predication parameters on mining subsidence [J].Journal of Jiaozuo Institute of Technology:Natural Science Edition，2001，20(4):253-257.

[17] 刘 芸.浅析Matlab绘图功能在高等数学中的应用[J].吉林省教育学院学报，2012(7)：57-58. Liu Yun.Application of Matlab drawing function in higher mathematics[J].Journal of Educational Institute of Jilin Province，2012(7):57-58.

[18] 英 英.基于MATLAB的图形图像处理系统的实现[D].呼和浩特：内蒙古大学，2013. Ying Ying.Realization of the Graphics Image Processing System Based on Matlab[D].Hohhot:Inner Monggulia University，2013.

[19] 徐光华.基于二次曲线拟合的隧道激光点云滤波方法及其应用[J].测绘通报，2015(5)：42-45. Xu Guanghua.Laser point cloud filtering and application in tunnel deformation monitoring based on quadratic curves fitting [J].Bulletin of Surveying and Mapping，2015(5):42-45.

[20] 顾 伟，谭志祥，邓喀中.基于Active X Automation的三维可视开采沉陷预计[J].金属矿山，2013(3)：119-122. Gu Wei，Tan Zhixiang，Deng Kazhong.3D visualization prediction of mining subsidence system based on Active X Automation [J].Metal Mine，2013(3):119-122.

[21] 查剑锋，郭广礼，赵海涛，等.概率积分法修正体系现状及发展展望[J].金属矿山，2008(1)：15-18. Zha Jiangeng，Guo Guangli，Zhao Haitao，et al.Present situation and prospect of correction system for probability integral method [J].Metal Mine，2008(1):15-18.

(责任编辑 王小兵)

Calculating on the Prediction Parameters of Mining Subsidence with Probability Integral Method Based on Matlab

Shen Zhen Xu Liangji Liu Zhe Qin Changcai

(SchoolofGeodesyandGeomatics，AnhuiUniversityofScience&Technology，Huainan232000，China)

The prediction parameters of mining subsidence are calculated by the probability integral method of the surface deformation data obtained by the observation stations established on the surface of mining working face，and the mining subsidence of the surrounding area of mining working face or the mining working face under the similar mining conditions are predicted to conduct evaluation and guidance on the mining operation.Therefore，obtaining the prediction parameters of mining subsidence with high precision is the precondition of prediction and inversion of mining subsidence prediction.Based on Matlab software，the deformation data of observation points are fitted by the least square method to calculate the prediction parameters of mining subsidence with probability integral method.Combing with the drawing tools of Matlab software，the mining subsidence visualization system with the functions of data loading，coordinate transformation，calculation parameters，the output of calculation results，prediction and inversion of mining subsidence is developed.Taking the 11316 working face of Xieqiao coal mine，Huainan city as the research example，according to the deformation data of the observation points of the surface observation stations，the prediction parameters of mining subsidence are calculated，and comparison between predicted parameters and measured parameters is conducted.The results show that the predicted parameters calculated by the mining subsidence visualization system is consistent with the basic rules of the mining subsidence in Huainan & Huaibei mining area，and the inversion results of the mining subsidence visualization system is identical to the measured parameters.The mining subsidence visualization system can provide reference for realizing the prediction and inversion of mining subsidence with high precision.

Mining subsidence，Probability integral method，Mining subsidence prediction system，Least square method，Matlab

2015-06-04

安徽省对外科技合作计划项目(编号：1503062020)，国家自然科学基金项目(编号：41472323)。

沈 震(1990—)，男，硕士研究生。通讯作者 徐良骥(1978—)，男，副教授，博士，硕士研究生导师。

TD325

A

1001-1250(2015)-09-170-05