2013年四川芦山MS7.0地震强地面运动模拟

药晓东 章文波

（中国北京100049中国科学院大学地球科学学院）



2013年四川芦山MS7.0地震强地面运动模拟

（中国北京100049中国科学院大学地球科学学院）

运用经验格林函数法模拟2013年4月20日芦山MS7.0地震的近场强地面运动． 在拟合过程中， 首先参考前人远场反演结果给出的滑动量分布特征和主震波形的包络线特征， 确定强震动生成区的大致范围和数量； 然后利用Somerville等提出的地震矩与凹凸体面积的经验关系式确定强震动生成区细小划分的初值， 继而利用遗传优化算法确定以上二者的最优值及其它震源参数． 将数值模拟波形与实际地震观测记录在时间域和频率域分别进行比较， 结果显示， 在所选取的30个观测台站中， 多数台站的数值模拟结果与实际观测结果符合得很好， 特别是大于1 Hz的高频部分． 断层面上有两个强震动生成区， 其位置与前人反演的滑动量集中分布区相一致， 而且强震动生成区规模比Somerville等获得的标度率估计值要小．

强地面运动 芦山MS7.0地震 经验格林函数法 震源参数 波形对比

引言

2013年4月20日在我国四川省雅安市芦山县境内发生了MS7.0地震， 这是继2008年汶川大地震后发生在龙门山断裂带的又一次显著的灾害性事件． 地震发生后， 我国地震工作者先后根据现场应急科考、 GPS观测数据、 远场地震数据和近震强震动数据发布了此次地震的发震构造模型、 震源机制解、 地震震源破裂过程、 精定位及其与汶川地震的关系等研究结果（陈运泰等， 2013； 王卫民等， 2013； 武艳强等， 2013； 谢祖军等， 2013； 徐锡伟等， 2013； 张勇等， 2013； 金明培等， 2014）． 此外， 孟令媛等（2014）利用随机震源模型模拟了芦山地震的烈度分布， 张冬丽等（2013）使用有限差分法模拟了其强地面运动特征． 但是这些工作都没有直接模拟近场强地面运动的具体波形和频谱， 而波形峰值、 持时及频谱特征是地震动的三要素．

近年来发生的破坏性大地震, 例如我国1999年台湾集集地震、 2008年汶川地震， 日本1995年神户地震、 2003年十胜（Tokachi）地震、 2011年东北（Tohoku）地震， 1999年土耳其Kocaeli地震, 2010年海地地震以及2010年智利大地震， 都展示给我们： 大地震产生的强地面运动是工程建筑物动力灾变的最主要原因， 是造成各类建筑物损毁甚至倒塌的直接原因， 是人员伤亡和各类次生灾害发生的主要诱因． 目前地震学和地震工程学研究人员已经认识到， 近场强地面运动预测对于减轻未来大地震所造成的灾害、 重大工程的抗震设计以及地震危险性分析均有极其重要的作用， 所以如何有效地预测破坏性大地震的强地面运动成为地震学和地震工程学领域中最为重要的课题之一．

目前预测未来大地震强地面运动的方法主要包括： ① 确定性的数值计算方法， 即利用计算机通过数值计算来实现仿真模拟， 包括运动学模拟和动力学模拟（Zhangetal, 2010； Ruiz, Madariaga, 2013）； ② 随机方法， 即基于地震点源ω2模型（Brune, 1970, 1971）， 利用随机震源理论来模拟地震的高频地面地震动， 或者采用改进的随机有限断层方法（Boore, 1983； Motazedian, Atkinson, 2005）； ③ 理论方法， 即以位移表示定理为基础， 以理论格林函数计算为核心的方法（Eringen, Suhubi, 1975； Aki, Richards， 1980）． 虽然以上3种方法中理论方法具有严格的数学物理意义， 但是目前只能计算水平成层的理论格林函数， 因此运用理论格林函数计算理论地震图还存在很大的局限． 这3种方法均有各自不足： 数值方法对计算资源的消耗比较大， 费时较多； 随机方法缺乏明确的物理意义； 理论方法在非水平成层和非均匀介质的计算中没有解析解， 如果借助数值计算则耗时较多． 为了克服这些不足， Hartzell（1978） 提出一种经验格林函数法----选取主震的小震（余震或前震）记录作为格林函数， 取代理论格林函数的计算， 通过一定的破裂方式进行叠加获得主震的地面运动记录． 由于小震记录已经包含了震源、 传播路径和局部场地效应的影响， 因此避免了计算理论格林函数的复杂性． 针对这一方法， 研究人员进行了深入研究并加以改进， 其中最重要的包括： Kanamori（1979）引入距离和辐射花样校正； Irikura（1983）根据大小地震的相似性， 将小震的选取转化为如何对小震进行较正， 并运用到实际大地震的强震动实例分析中， 由此该方法得到了广泛应用（Joyner, Boore, 1986; 罗奇峰, 1989; Danetal, 1990; 张有兵， 章文波， 2010； 药晓东等， 2015）． 本文利用这一方法对2013年芦山MS7.0地震的强地面运动进行模拟， 旨在为未来大地震的地震动预测和该地区的工程抗震设计提供可靠依据．

1 经验格林函数法原理

利用理论方法计算地震图的核心是计算格林函数， 虽然目前格林函数的计算取得了一些进展（Kennett, 1980; Bouchon, 1981； Chen, 1995, 1996）， 但真实地球的复杂性， 使得三维复杂构造的格林函数一直很难确定． 为了克服这一难题， Hartzell（1978）提出了利用大地震后余震记录作为一种经验格林函数来模拟大震记录的方法． 其基本思路是： 一个小地震记录（前震或者余震）， 由于已经包含了震源、 传播路径和局部场地信息， 所以近似视为一对“源点-接收点”之间的格林函数， 通过这种格林函数与变化的震源空间时间函数作卷积， 可以合成大地震所引起的地面运动. 这种合成方法是半经验性的， 所以被称为“经验格林函数法”． 该方法的优势在于格林函数取自小震记录， 自然包括了真实地球介质从震源、 传播路径到接受点的场地条件影响的主要信息， 从而避免了理论格林函数的计算， 减小了计算量， 加快了计算速度．

经验格林函数法最初的假定是一个台站记录到覆盖整个破裂面的可视为点源的小震记录， 则可以通过叠加模拟出该台站的大震记录（Hartzell, 1978）． 然而实际情况是台站上的记录远远不足， 所以该方法难以实现． 为了使该方法在实践中得到更广泛的应用， Kanamori和Irikura先后作出了重要的改进． Kanamori（1979）考虑到目标地震具有一定断层规模且由许多小震源组成， 所以即使个别小震记录可以选作断层面上的点源记录， 也要考虑到位置因素， 因此必须进行距离和辐射图案校正． 此外， 为了使小震记录作为格林函数， 要求其拐角频率高于地震动的目标最高频率， 即要求所选择的小震破裂尺度足够小， 而且记录的信噪比足够高． 由于小震破裂尺度足够小和记录信噪比足够高之间存在着固有矛盾， 所以此条件不容易满足． Irikura（1983）依据对大小地震震源参数的统计研究结果， 提出了大小地震满足相似律的假设， 并将大地震中的子源和所利用的小震的位错函数均视为斜坡函数， 则大地震产生的地面运动可由对子源在断层上的二重求和转换为对小震在断层上和时间域内的三重求和． 基于这些假设， 该方法放宽了对小震记录的限制； 而且把问题从选择什么样的小震作为格林函数转换为如何合理地对小震记录进行修正以得到大震中的子源贡献， 这使得这一方法得到了广泛的应用（Joyner, Boore, 1986; 罗奇峰, 1989; Danetal, 1990; 张有兵， 章文波， 2010； 药晓东等， 2015）．

本文主要采用Irikura（1983）所改进的方法， 并针对当所选取的“小震”较大和强震动生成区不唯一时， 如何划分主断层上的子断层作了改进． 图1a为经验格林函数法示意图． 该方法基本原理的数学表达为

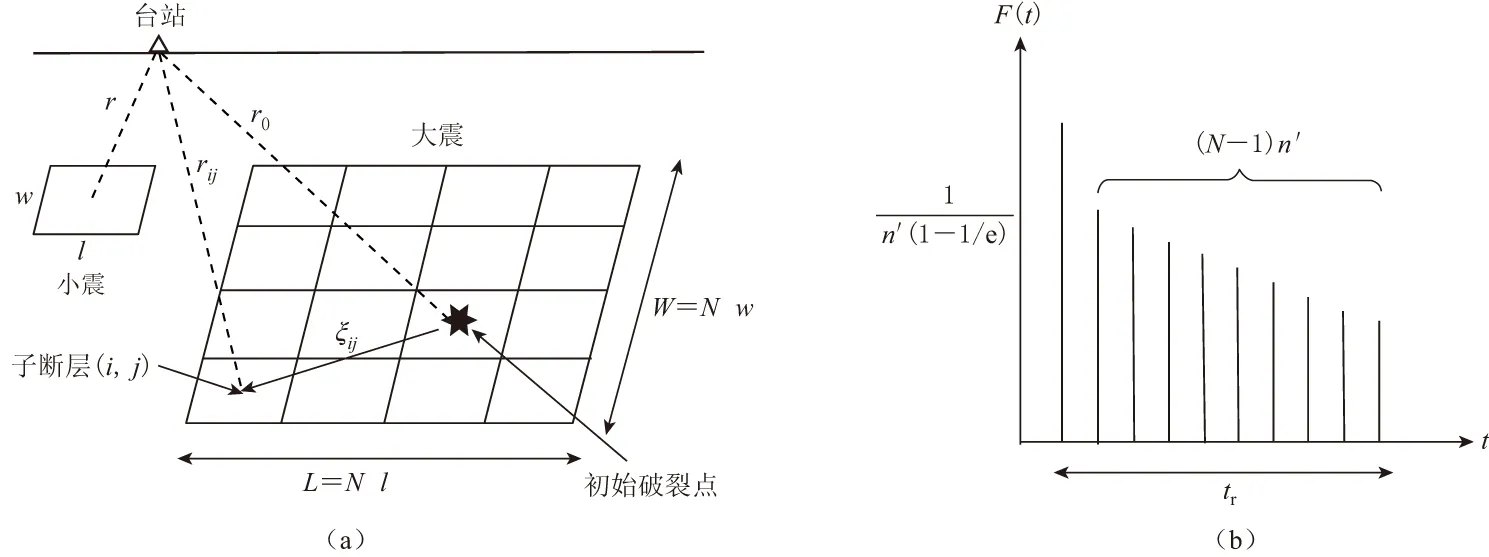
图1 经验格林函数法示意图

（1）

（2）

（3）

式中：U（t）和u（t）分别为主震记录和小震记录， 这里将u（t）近似看作格林函数来拟合U（t）；r，r0，rij和ξij分别表示小震到台站的距离、 主震初始破裂点到台站的距离、 主震断层上子断层（i，j）到台站的距离， 以及主震初始破裂点到子断层（i，j）的距离；β为剪切波速度；VR为破裂传播速度；N为主震断层划分为细小子断层的特征数， 通常主震断层划分为小断层的数目用N×N表示；C为地震尺寸和应力降的参数， 与N联合在一起表示大小地震之间规模与应力降之比； 由于主震和小震在震源时间函数和频率上存在差异， 所以在模拟时需要对小震记录的频谱进行调整， 式中F（t）是一个滤波窗函数， 通过与小震记录作卷积起到调整小震频谱的作用， 其形状参见图1b；n′为对频率上限进行调整的参数．

从经验格林函数法的原理和数学表达中可以看出， 该方法的关键在于经验格林函数小震的选取． 如果小震记录能够在震源过程、 传播路径和场地条件等3方面与主震一致， 那么通过一定的叠加则可以很好地合成主震记录． 但在实际应用中， 对于同一个台站的记录， 通常只有场地条件最容易满足， 而传播路径和震源信息则无法实现一致， 所以须综合考虑小震与主震的差异， 通过距离和频率校正来生成可靠的记录（张有兵， 章文波， 2010； 药晓东等， 2015）．

2 芦山MS7.0地震分析

2.1 经验格林函数小震的选取

如前文所述， 经验格林函数法的优势在于包含了震源过程、 传播路径和场地条件上的主要信息， 因此拟合的关键在于小震的选取是否恰当． 因为小震与主震的空间位置和震源机制是否相似决定了拟合的优劣， 所以我们将震源位置和震源机制作为选择小震的标准． 此外拟合台站的数量和覆盖范围也是我们考虑的因素， 拟合台站数量过少或者不能覆盖主震断层的不同方位也是需要避免的． 为了满足拟合台站数量和记录信噪比， 本文只考虑M≥3.0的小震．

芦山地震后， 不同研究小组利用全球测震资料发布了此次地震的震源机制． 哈佛大学全球质心矩张量目录（Dziewonskietal, 1981; Ekströmetal, 2012）给出的震源机制为： 断层走向212°， 倾角42°， 滑动角100°， 深度21.9 km， 地震矩1.02×1019N·m，MW6.6 （GCMT， 2013）； 美国地质调查局地震情报中心给出的震源机制为： 断层走向198°， 倾角33°， 滑动角71°， 深度12 km， 地震矩1.0×1019N·m，MW6.6 （USGS， 2013）； 中国地震局地球物理研究所陈运泰院士研究组给出的震源机制为： 断层走向220°， 倾角35°， 滑动角95°， 深度12 km， 地震矩1.6×1019N·m，MW6.7 （中国地震台网中心， 2013）． 不同机构给出的震源机制结果均反映了震源的逆冲特征， 本文将主要参考国内机构给出的结果， 即断层走向220°， 倾角35°， 滑动角95°—101°， 深度12—13 km， 地震矩（1.4—1.6）×1019N·m． 国家强震动台网中心获得了此次地震的主、 余震记录， 其中主震记录363条， 余震记录3300多条， 余震震级范围为MS2.3—5.4， 所有地震记录均为三分向加速度记录， 采样频率均为200 Hz．

表1 主震和作为经验格林函数的余震的震源位置和震源机制Table 1 Focal mechanisms and locations of the main shock and the aftershock used as EGF in this study

表2 强震动台站位置信息Table 2 Locations of the 30 strong motion stations used in this study

根据以上信息， 并结合哈佛大学全球质心矩张量目录以及吕坚等（2013）给出的余震震源机制和定位信息， 本文筛选出一次MW4.8余震作为经验格林函数小震. 主震和所选取余震的震源参数见表1， 记录地震数据的台站信息见表2， 主震、 余震和台站的空间分布如图2所示． 此次模拟涉及的台站为30个． 尽管另外两个台站（051LSL乐山凌云台和051MCL沐川利店台）也获取了主、 余震记录， 但由于这两个台站的主震记录异常而被剔除． 图3给出了典型的余震记录加速度时程及其傅里叶谱（051BXD和051CDZ台站）． 我们按以下步骤对数据进行统一处理： 首先进行基线校正， 然后利用凯泽（Kaiser）窗带通滤波器对记录进行滤波， 带通频率范围为0.2—20 Hz．

图2 主震、 余震和台站空间分布图

2.2 模型参数估计

芦山地震发生后， 研究人员利用远场地震数据（王卫民等， 2013； 张勇等， 2013； 赵翠萍等， 2013）以及GPS数据与近场地震数据联合（金明培等， 2014）反演了汶川地震的断层面滑动量．

王卫民等（2013）的断层模型为： 主断层走向205°， 倾角38.5°， 断层规模66 km×35 km． 反演结果显示此次地震为逆冲事件， 最大滑动量为1.59 m， 最大滑动量所在的凹凸体基本位于断层中部， 在震源深度偏上位置， 在凹凸体周围同时还分布着3个较小的滑动量集中区（图4a）． 张勇等（2013）的断层模型为： 主断层走向219°， 倾角33°， 断层规模60 km×45 km． 反演结果显示这是一个以逆冲为主、 但兼具比汶川地震还小的右旋走滑分量的地震， 最大滑动量为1.3 m， 最大滑动量所在的凹凸体基本位于断层中部， 包括了震源所在位置， 在凹凸体西南方、 断层面下缘同时还有另一个较小的滑动量集中区（图4b）． 赵翠萍等（2013）的断层模型为： 主断层走向220°， 倾角35°， 断层规模100 km×45 km． 反演结果显示此次地震破裂自起始破裂点向地表快速发展, 呈双侧破裂的逆冲事件， 凹凸体在起始破裂点之上40 km×30 km 区域, 最大滑动量为1.8 m， 在震中地表的北东方向有一个滑动量为0.4 m左右的区域（图4c）． 金明培等（2014）的断层模型为： 主断层走向212°， 倾角35°—54°， 断层规模60 km×39 km． 反演结果显示此次地震以逆冲为主， 最大滑动量为1.1 m， 最大滑动量所在的凹凸体基本位于断层中部， 包含了震源所在位置， 在凹凸体周围同时还分布着3个较小的滑动量集中区（图4d）． 无论是远震台站反演， 还是GPS与近场强震联合反演， 其结果都有共同的特征， 即在断层面中心位置附近有唯一的凹凸体， 其最大滑动量为1.1—1.8 m．

不同的反演结果均显示芦山地震的震源机制比较一致， 同时反演给出的震源过程也比较简单． 此外由记录到的加速度波形可以看出， 大多数台站的记录只体现出一个波包的整体特征， 这也说明芦山地震的发震过程比较简单． 但对所有的主震记录进行观察和分析时， 发现部分台站的记录体现出两个明显的波包特征． 以051LSF台站记录为例（图5）， 从包络线上可以看到EW和UD分量存在间隔为7—8 s的两个明显波包， 在EW和UD分量对应的第二个波包处， NS分量也有个明显的波包出现， 但在EW和UD分量的第一个波包位置， NS分量分裂为两个较小的波包． 因此可以初步判断芦山地震的强震动生成不是一次单一事件， 而是由至少两次事件， 即至少两个强震动生成区的发震所引起的． 由前文远场反演的滑动量分布可以看出这两个强震动生成区的震源机制相互一致， 因此考虑选择一个小地震记录作为经验格林函数． 已有的反演结果也显示， 在芦山主震的断层面上有一个主要的凹凸体和1—3个较小的局部滑动显著区（王卫民等， 2013； 张勇等， 2013； 赵翠萍等， 2013； 金明培等， 2014）， 因此本文构建的基本模型为两个强震动生成区， 其中较大的生成区位于震源附近， 较小的在其周围． 对于是否需要增加强震动生成区的数量则应根据实际模拟来确定， 同时参考前文的反演断层模型， 本文将事件发生的断层设定为66 km×35 km． 由于芦山地震震源机制变化较小， 所以模型中仅选用了同一个经验格林函数余震． 模型中还涉及到强震动生成区的位置， 本文主要参考王卫民等（2013）的反演结果， 同时也参考了其它反演结果， 最终的确切位置由遗传算法优化搜索获取．

图3 051BXD（a）和051CDZ（b）台站记录到的余震加速度时程（上）及其傅里叶谱与噪声谱（下）

图4 芦山地震断层面上的滑动量分布

图5 051LSF台站记录的芦山主震加速度时程. 图中数字为记录到的加速度峰值

确定强震动生成区的可能位置后， 还要确定强震动生成区划分成子块的数量N． 以往主要根据地震的相似性， 包括几何形状、 应力降、 平均位移和上升时间等， 推导出N的确定方法以及改进的震源谱比法（Irikura, 1983; Irikura, Kamae, 1994）． 但是由于这些方法在强震动生成区不唯一， 无法分配不同强震动生成区的大小， 因此在芦山地震模拟的实例中， 我们首先借鉴凹凸体与地震矩之间的标度关系进行初值估计， 然后再利用优化算法最终确定N值．

Somerville等（1999）根据15个MW5.6—7.2地震的研究结果给出了地震矩与凹凸体总面积的经验关系为

（4）

式中：M0为地震矩， 单位为N·m；Aa为凹凸体总面积， 单位为km2． 根据哈佛大学全球质心矩张量目录给出的结果： 芦山地震主震标量地震矩为1.02×1019N·m， 小震的标量地震矩为2.15×1016N·m， 两者凹凸体总面积之比为60.8． 据此假设主震与小震的强震动生成区的比值为61， 此即为两个强震动生成区细小划分总和的初始估计值． 由于不同研究小组给出的地震矩存在一些差别， 其中较大的一个是中国地震局地球物理研究所陈运泰院士研究组给出的1.6×1019N·m （中国地震台网中心， 2013）， 求出的相应比值为82． 为此， 我们将主震与小震的凹凸体面积之比的初始范围设定为61—82， 具体划分则要借助遗传算法进行优化搜索． 这里之所以选择遗传算法是因为本文的模拟问题是多极值问题， 智能优化算法是相对更合理的解决策略． 根据以往将强震动生成区划分为N×N块的方法， 我们也将每个强震动生成区的子网格在走向方向和倾向方向按相同数量进行划分．

在确定强震动生成区的大小时， 我们首先设定强震动生成区划分的子断层长宽相等， 然后采用遗传算法（Carroll, 2001）在0.1—5 km范围内进行搜索． 在确定断层破裂速度时参考相关研究， 将剪切波速度设定为3.5 km/s， 同时将断层破裂速度设定为2.1—3.6 km/s．这是因为目前研究结果表明， 破裂过程的平均速度一般为剪切波速的60%—90%， 但对于个别大地震的破裂过程， 由于其局部某个时段有可能发生超剪切破裂（张海明， 2006）， 因此放宽了搜索范围． 对于其它震源参数， 依然借助遗传算法搜索得到．

在利用遗传算法优化搜索参数时， 衡量参数最优的标准是使模拟波形与真实记录波形之间的适配函数达到最小． 本文使用的适配函数是对加速度、 速度和位移波形的三分量全部进行比较， 且采用等权重相加． 由于时间域波形比较复杂， 所以我们采用比较包络线的方式， 具体形式为

Emis=

（5）

式中，eobs-acc，eobs-vel和eobs-disp分别表示观测的加速度、 速度和位移的包络线；esyn-acc，esyn-vel和esyn-disp分别表示拟合的加速度、 速度和位移的包络线．

3 结果与讨论

通过模型参数的估计和遗传算法优化搜索确定了最优模型， 模型参数见表3， 其中N1=8，N2=4， 子断层划分的总和为80， 介于初始估计值61—82之间． 强震动生成区1和强震动生成区2的面积分别为64 km2和16 km2， 具体位置和面积大小见图6， 强震动生成区的总面积为80 km2， 比用式（4）估计的109 km2， 即Somerville等（1999）获得的标度率的估计值要小． 继Somerville等（1999）研究标度率后， Irikura和Miyake（2011）也总结了类似的标度率， 但其总结的主要是破裂面积与地震矩之间的标度关系． 我们借助Somerville等（1999）获得的凹凸体与地震矩之间的标度关系式（4）， 以及破裂面与地震矩之间的关系得到

（6）

表3 最优模型参数和遗传算法搜索范围Table 3 The optimal parameters of determined model and their search scopes for genetic algorithm

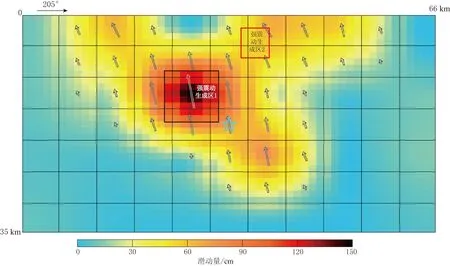
图6 基于王卫民等（2013）的反演结果构建的强震动震源模型

式中：M0为地震矩， 单位为N·m；A为破裂面积， 单位为km2． 这样可以估计出破裂面积与凹凸体面积之比为4.46， 借助该比值， 我们将Irikura和Miyake（2011）总结的破裂面积与地震矩之间的标度关系转化为凹凸体总面积与地震矩之间的标度关系, 即

（7）

（8）

Aa=1.19×10-18M0，M0≥7.5×1020,

（9）

式中：M0为地震矩， 单位为N·m；Aa为凹凸体总面积， 单位为km2． 该标度率为三段形式， 见图7a的黑色实线． 可以看出， 式（4）与式（7）表达相同， 意味着中等震级地震在Somerville等（1999）和Irikura和Miyake（2011）中服从相同的标度关系， 但从式（8）和式（9）可以看出， Irikura和Miyake（2011）对大地震和巨大地震所总结的标度关系与Somerville等（1999）出现了差异， 这是因为在总结标度关系时Irikura和Miyake（2011）加入了更多的地震数据， 尤其是大地震和巨大地震的数据． 虽然此次模拟比式（4）中对应的面积要小， 但式（8）同样出现了比式（4）面积小的趋势． 因此此次模拟结果佐证了式（8）的趋势， 也为大地震的标度率总结提供了一则实例依据．

图7 强震动生成区面积（a）和上升时间（b）与地震矩的标度关系

由图6可以看出， 最优模型的强震动生成区1的初始破裂点几乎位于正中心， 然后向两侧破裂， 这也验证了芦山地震由震源发震， 向双侧破裂的特征； 同时与应力降有关的参数C1和C2分别为1.6和0.7， 反映了强震动生成区1的应力降比强震动生成区2的要大； 而两个强震动生成区的上升时间均为1.0 s， 与Somerville等（1999）获得的标度率的估计值0.95 s非常接近（图7b）．

从图6可以看出， 强震动生成区1与凹凸体位置一致， 体现了高频能量与低频能量的主要生成区域是相似的； 但强震动生成区2却与其它反演结果存在差别， 这源于本文的模拟频率范围与确定性方法的频率范围不同， 本文的频率范围为1—20 Hz， 而确定性方法由于其数值计算的频率受计算能力和耗时的影响， 往往低于1 Hz， 所以出现两者不同的可能性非常大．

图8给出了加速度波形的模拟结果． 可以看出， 051BXD台站的EW分量达到了1005.4 cm/s2， 是我国内陆地区观测到的首个超过1g（1g=9.8×102m/s2）的记录． 该台站无论是时间域还是频率域均拟合得很好． 水平加速度峰值超过100 cm/s2的台站共有12个， 其中10个台站（051BXM， 051BXY， 051BXZ， 051HYY， 051LDL， 051LSF， 051TQL， 051YAD， 051YAL和051YAM）在时间域和频率域均拟合得很好， 只有2个台站（051PJD和051QLY）的估计值明显偏小． 这种偏小估计值也出现在051CDZ和051DJZ台站上. 这4个台站刚好位于芦山地震主震断层的北东向， 而且这种明显偏小的估计值并未出现在其它方位的台站上． 结合哈佛大学质心矩张量目录给出的芦山地震主、 余震的滑动角分别为100°和74°（表1）， 可以看出， 主震体现为逆冲为主兼微小右滑机制， 而余震体现为逆冲为主兼微小左滑机制. 这体现了余震震源机制对拟合的影响直接关系到加速度峰值和幅值谱的大小． 拟合结果中最差的是051QLY台站的EW分量， 无论在时间域或频率域均偏离较大． 其原因一方面由于震源机制的影响， 另一方面与该记录的信噪比有关（图9）． 通过051QLY台站EW分量的信噪比与其它记录的信噪比对比（如051YAM台站的EW分量）可以看出， 051QLY台站的EW分量在1 Hz左右的信噪比很低， 因此在拟合过程中会影响结果． 在分析过程中我们也考虑过在断层靠近北东向的位置增加一个强震动生成区， 这样可以弥补051PJD台站估计值偏小的问题， 但增加一个强震动生成区会增大对其它台站的贡献， 导致其它台站模拟结果偏大， 因此我们对两个强震动生成区的模型并未作调整．

图8 各台站加速度时程（a）和加速度傅里叶谱（b）的观测记录（黑色）与最优模型的拟合结果（灰色）对比（Ⅰ）

图8 各台站加速度时程（a）和加速度傅里叶谱（b）的观测记录（黑色）与最优模型的拟合结果（灰色）对比（Ⅱ）

图8 各台站加速度时程（a）和加速度傅里叶谱（b）的观测记录（黑色）与最优模型的拟合结果（灰色）对比（Ⅲ）

结合模拟过程中的计算， 我们发现拟合对小震的定位非常敏感， 而对主余震断层的几何长宽的敏感度较差． 这一点可能是由于主、 余震断层的几何形状比较相似， 而且多数台站的震中距要大于断层几何尺度的缘故．

4 结论

本文利用经验格林函数法对芦山地震的30个台站进行模拟研究， 选择一个余震记录作为经验格林函数， 采用两个强震生成区进行模拟， 结果显示在时间域和频率域， 尤其是大于1 Hz的高频部分， 多数台站均拟合得很好． 对于加速度峰值超过100 cm/s2的台站， 特别是051BXD台站， 其拟合结果非常好， 体现出经验格林函数法的优势所在， 也说明了经验格林函数法的可靠性．

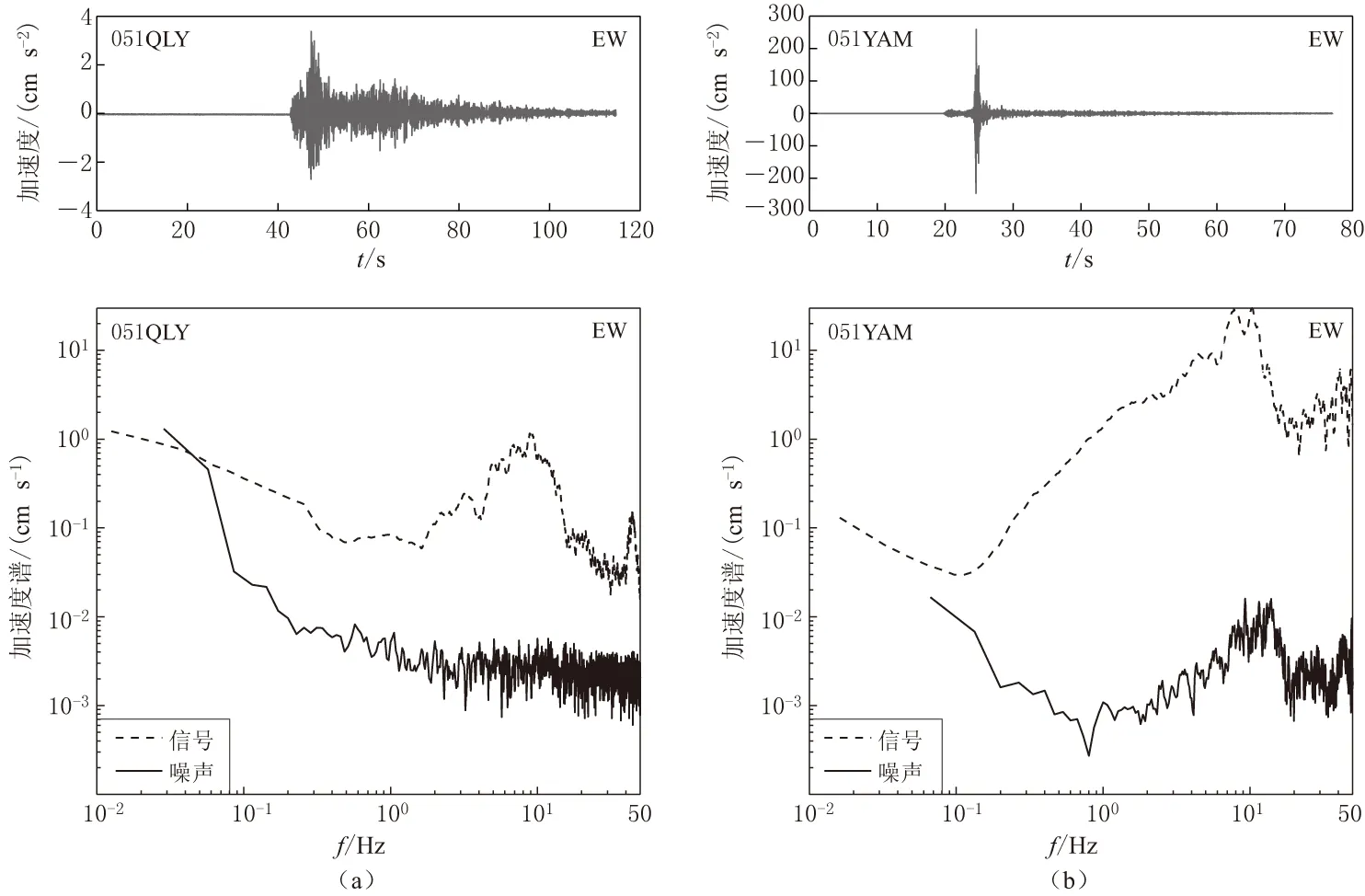
图9 051QLY（a）和051YAM（b）台站记录到的余震加速度时程（上）及其傅里叶谱与噪声谱（下）

小震震源机制对模拟结果的影响非常明显， 其与目标地震的震源机制越接近, 则模拟结果越好． 我们还发现拟合结果对小震的定位非常敏感， 而我们所掌握的小震资料是有限的， 因此关于小震震源机制和精确定位的相关研究， 对强震动模拟非常重要． 同时小震记录的信噪比也是影响模拟的重要因素．

本文确定的强震动生成区的模型参考了远场反演的模型， 但最终结果与其又有一定的差别， 因此总结两者之间的异同， 寻找两者之间的关联对震源研究和强震动模拟具有重要的意义．

虽然经验格林函数法对强地面运动的模拟非常有效， 但是对于预测未来大地震的强地面运动， 还需要对大量的地震实例和模拟进行总结， 对小震的震级、 定位、 震源机制以及主余震震源的差异等都需要进一步研究． 同时地震标度率的总结是未来灾害性地震动预测的基础， 是特征化模型的重要组成部分， 因此地震标度率尤其是大地震的标度关系， 需要加入更多的地震实例， 进行更深入的研究．

陈运泰, 杨智娴, 张勇, 刘超. 2013. 从汶川地震到芦山地震[J]. 中国科学: 地球科学, 43（6）: 1064--1072.

Chen Y T, Yang Z X, Zhang Y, Liu C. 2013. From 2008 Wenchuan earthquake to 2013 Lushan earthquake[J].ScientiaSinicaTerrae, 43（6）: 1064--1072 （in Chinese）.

金明培, 汪荣江, 屠泓为. 2014. 芦山7级地震的同震位移估计和震源滑动模型反演尝试[J]. 地球物理学报, 57（1）: 129--137.

Jin M P, Wang R J, Tu H W. 2014. Slip model and co-seismic displacement field derived from near-source strong motion records of the LushanMS7.0 earthquake on 20 April 2013[J].ChineseJournalofGeophysics, 57（1）: 129--137 （in Chinese）.

罗奇峰. 1989. 近场加速度的半经验合成[D]. 哈尔滨: 中国地震局工程力学研究所： 8--14.

Luo Q F. 1989.TheSemi-EmpiricalSynthesisofNear-FieldGroundMotions[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration: 8--14 （in Chinese）.

吕坚, 王晓山, 苏金蓉, 潘林山, 李正, 尹利文, 曾新福, 邓辉. 2013. 芦山7.0级地震序列的震源位置与震源机制解特征[J]. 地球物理学报, 56（5）: 1753--1763.

Lü J, Wang X S, Su J R, Pan L S, Li Z, Yin L W, Zeng X F, Deng H. 2013. Hypocenter location and source mechanism of theMS7.0 Lushan earthquake sequence[J].ChineseJournalofGeophysics, 56（5）: 1753--1763 （in Chinese）.

孟令媛, 周龙泉, 刘杰. 2014. 2013年四川芦山MS7.0地震近断层强地面运动模拟及烈度分布估计[J]. 地球物理学报, 57（2）: 441--448.

Meng L Y, Zhou L Q, Liu J. 2014. Estimation of the near-fault strong ground motion and intensity distribution of the 2013 Lushan, Sichuan,MS7.0 earthquake[J].ChineseJournalofGeophysics, 57（2）: 441--448 （in Chinese）.

王卫民, 郝金来, 姚振兴. 2013. 2013年4月20日四川芦山地震震源破裂过程反演初步结果[J]. 地球物理学报, 56（4）: 1412--1417.

Wang W M, Hao J L, Yao Z X. 2013. Preliminary result for rupture process of Apr. 20, 2013, Lushan earthquake, Sichuan, China[J].ChineseJournalofGeophysics, 56（4）: 1412--1417 （in Chinese）.

武艳强, 江在森, 王敏, 车时, 廖华, 李强, 李鹏, 杨永林, 向和平, 邵志刚, 王武星, 魏文薪, 刘晓霞. 2013. GPS监测的芦山7.0级地震前应变积累及同震位移场初步结果[J]. 科学通报, 58（20）: 1910--1916.

Wu Y Q, Jiang Z S, Wang M, Che S, Liao H, Li Q, Li P, Yang Y L, Xiang H P, Shao Z G, Wang W X, Wei W X, Liu X X. 2013. Preliminary results of the co-seismic displacement and pre-seismic strain accumulation of the LushanMS7.0 earthquake reflected by the GPS surveying[J].ChineseScienceBulletin, 58（20）: 1910--1916 （in Chinese）.

谢祖军, 金笔凯, 郑勇, 葛粲, 熊熊, 熊诚, 许厚泽. 2013. 近远震波形反演2013年芦山地震震源参数[J]. 中国科学: 地球科学, 43（6）: 1010--1019.

Xie Z J, Jin B K, Zheng Y, Ge C, Xiong X, Xiong C, Hsu H T. 2013. Source parameters inversion of the 2013 Lushan earthquake by combining teleseismic waveforms and local seismograms[J].ScientiaSinicaTerrae, 43（6）: 1010--1019 （in Chinese）.

徐锡伟, 闻学泽, 韩竹军, 陈桂华, 李传友, 郑文俊, 张世民, 任治坤, 许冲, 谭锡斌, 魏占玉, 王明明, 任俊杰, 何仲, 梁明剑. 2013. 四川芦山7.0级强震: 一次典型的盲逆断层型地震[J]. 科学通报, 58（20）: 1887--1893.

Xu X W, Wen X Z, Han Z J, Chen G H, Li C Y, Zheng W J, Zhang S M, Ren Z K, Xu C, Tan X B, Wei Z Y, Wang M M, Ren J J, He Z, Liang M J. 2013. LushanMS7.0 earthquake: A blind reserve-fault earthquake[J].ChineseScienceBulletin, 58（20）: 1887--1893 （in Chinese）.

药晓东, 章文波, 于湘伟. 2015. 2008年汶川8.0级大地震近场强地面运动的模拟[J]. 地球物理学报, 58（3）: 886--903.

Yao X D, Zhang W B, Yu X W. 2015. Simulation of near-field strong ground motion caused by the 2008MS8.0 Wenchuan earthquake[J].ChineseJournalofGeophysics, 58（3）: 886--903 （in Chinese）.

张冬丽, 黄蓓, 张献兵, 徐锡伟, 郑文俊. 2013. 基于有限断层模型的芦山“4·20”7.0级强烈地震强地面运动特征[J]. 地震地质, 35（2）: 423--435.

Zhang D L, Huang B, Zhang X B, Xu X W, Zheng W J. 2013. Strong ground motion distribution and simulation based on finite fault model of Lushan 7.0 earthquake on April 20, 2013[J].SeismologyandGeology, 35（2）: 423--435 （in Chinese）.

张海明. 2006. 复杂断层系统动力学破裂的理论研究和地表影响下的超剪切破裂问题的初步研究[D]. 北京: 北京大学地球科学与空间学院： 1--5.

Zhang H M. 2006.TheoreticalStudyonDynamicsRupturesonComplexFaultSystemsandPreliminaryStudyonSupershearRupturesUndertheEffectofGround[D]. Beijing: School of Earth and Space Sciences, Peking University: 1--5 （in Chinese）.

张勇, 许力生, 陈运泰. 2013. 芦山4·20地震破裂过程及其致灾特征初步分析[J]. 地球物理学报, 56（4）: 1408--1411.

Zhang Y, Xu L S, Chen Y T. 2013. Rupture process of the Lushan 4·20 earthquake and preliminary analysis on the disaster causing mechanism[J].ChineseJournalofGeophysics, 56（4）: 1408--1411 （in Chinese）.

张有兵, 章文波. 2010. 用经验格林函数法模拟2008年日本岩手—宫城地震的强地面运动[J]. 地震学报, 32（3）: 320--331.

Zhang Y B, Zhang W B. 2010. Strong ground motion simulation of the 2008 Iwate-Miyagi, Japan, earthquake using empirical Green’s function method[J].ActaSeismologicaSinica, 32（3）: 320--331 （in Chinese）.

赵翠萍, 周连庆, 陈章立. 2013. 2013年四川芦山MS7.0级地震震源破裂过程及其构造意义[J]. 科学通报, 58（20）: 1894--1900.

Zhao C P, Zhou L Q, Chen Z L. 2013. Source rupture process of LushanMS7.0 earthquake, Sichuan, China and its tectonic implication[J].ChineseScienceBulletin, 58（20）: 1894--1900 （in Chinese）.

中国地震台网中心. 2013. 四川省雅安市芦山县7.0级地震[EB/OL]. [2015-06-10]. http:∥news.ceic.ac.cn/CC20130420080246.html.

China Earthquake Networks Center. 2013.MS7.0 earthquake occurred in Lushan, Ya’an city, Sichuan Province[EB/OL]. [2015-06-10]. http:∥news.ceic.ac.cn/CC20130420080246.html （in Chinese）.

Aki K, Richards P G. 1980.QuantitativeSeismology:TheoryandMethods[M]. San Francisco: W H Freeman and Company: 63--113.

Boore D M. 1983. Stochastic simulation of high-frequency ground motions based on seismological model of the radiated spectra[J].BullSeismolSocAm, 73（6A）: 1865--1894.

Bouchon M. 1981. A simple method to calculate Green’s functions for elastic layered media[J].BullSeismolSocAm, 74（4）: 959--971.

Brune J R. 1970. Tectonic stress and the spectra of seismic shear waves from earthquakes[J].JGeophysRes, 75（26）: 4997--5009.

Brune J R. 1971. Correction to “Tectonic stress and the spectra of seismic shear waves from earthquakes”[J].JGeophysRes, 76（20）: 5002.

Carroll D L. 2001. FORTRAN genetic algorithm （GA） driver[EB/OL]. [2015-06-10]. http:∥www.cuaerospace.com/Technology/GeneticAlgorithm/GADriverFreeVersion.aspx.

Chen X F. 1995. Seismogram synthesis for multi-layered media with irregular interfaces by global reflection/transmission matrices method: Ⅱ. Applications for 2D SH case[J].BullSeismolSocAm, 85（4）: 1094--1106.

Chen X F. 1996. Seismogram synthesis for multi-layered media with irregular interfaces by global reflection/transmission matrices method: Ⅲ. Theory for P-SV case[J].BullSeismolSocAm, 86（2）: 389--405.

Dan K, Watanabe T, Tanaka T, Sato R. 1990. Stability of earthquake ground motion synthesized by using different small-event records as empirical Green’s functions[J].BullSeismolSocAm, 80（6A）: 1433--1455.

Dziewonski A M, Chou T A, Woodhouse J H. 1981. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity[J].JGeophysRes, 86（B4）: 2825--2852.

Ekström G, Nettles M, Dziewonski A M. 2012. The global CMT project 2004—2010: Centroid-moment tensors for 13017 earthquakes[J].PhysEarthPlanetInter, 200: 1--9.

Eringen A, Suhubi E. 1975.Elastodynamics，VolumeⅡ:LinerTheory[M]. New York: Academic Press, Inc: 717--834.

GCMT. 2013. Global CMT catalog[EB/OL]. [2015-06-10]. http:∥www.globalcmt.org/cgi-bin/globalcmt-cgi-bin/CMT4/form?itype=ymd&yr=2013&mo=4&day=20&otype=ymd&oyr=2013&omo=4&oday=21&jyr=1976&jday=1&ojyr=1976&ojday=1&nday=1&lmw=0&umw=10&lms=0&ums=10&lmb=0&umb=10&llat=-90&ulat=90&llon=-180&ulon=180&lhd=0&uhd=1000<s=-9999&uts=9999&lpe1=0&upe1=90&lpe2=0&upe2=90&list=0.

Hartzell S H. 1978. Earthquake aftershocks as Green’s functions[J].GeophysResLett, 5（1）: 1--4.

Irikura K. 1983. Semi-empirical estimation of strong ground motions during large earthquakes[J].BullDisasPrevResInst, 33（298）: 63--104.

Irikura K, Kamae K. 1994. Estimation of strong ground motion in broad-frequency band based on a seismic source scaling model and an empirical Green’s function technique[J].AnnGeophys, 37（6）: 25--47.

Irikura, K, Miyake H. 2011. Recipe for predicting strong ground motion from crustal earthquake scenarios[J].PureApplGeophys, 168（1/2）: 85--104.

Joyner W B, Boore D M. 1986. On simulating large earthquakes by Green’s function addition of smaller earthquakes[C]∥EarthquakeSourceMechanics. Washington: American Geophysical Union: 269--274.

Kanamori H. 1979. A semi-empirical approach to prediction of long-period ground motions from great earthquakes[J].BullSeismolSocAm, 69（6）: 1645--1670.

Kennett B L N. 1980.Seismic waves in stratified halfspace: Ⅱ. Theoretical seismograms[J].GeophysJInt, 61（1）: 1--10.

Motazedian D, Atkinson G M. 2005. Stochastic finite-fault modeling based on a dynamic corner frequency[J].BullSeismolSocAm, 95（3）: 955--1010.

Ruiz S, Madariaga R. 2013. Kinematic and dynamic inversion of the 2008 northern Iwate earthquake[J].BullSeismolSocAm, 103（2A）: 694--708.

Somerville P, Irikura K, Graves R, Sawada S, Wald D, Abrahamson N, Iwasaki Y, Kagawa T, Smith N, Kowada A. 1999. Characterizing crustal earthquake slip models for the prediction of strong ground motion[J].SeismolResLett, 70（1）: 59--80.

USGS. 2013.M6.6: 56 km WSW of Linqiong, China[EB/OL]. [2015-06-10]. http:∥earthquake.usgs.gov/earthquakes/eventpage/usb000gcdd#general_summary.

Zhang W B, Iwata T, Kojiro K. 2010. Dynamic simulation of the 1999 Chi-Chi, Taiwan, earthquake[J].JGeophysRes, 115（B4）: B04305.

Strong ground motion simulation for the 2013MS7.0 Lushan, China, earthquake

（CollegeofEarthScience,UniversityofChineseAcademyofSciences,Beijing100049,China）

The near source strong ground motions of the 2013MS7.0 Lushan, China, earthquake were simulated using empirical Green’s function （EGF） method. At first, we estimated the amount and location of strong motion gene-ration areas （SMGAs） based on the characteristics of both slip distributions from far-field seismic inversion and the envelopes of recorded acceleration from the main shock, and determined the amount of subfaults on SMGAs referring to the scaling law of asperity areaversusseismic moment introduced by Somervilleetal. Then, we implemented the genetic algorithm searching for the optimized value of above two and other source parameters. Based on the source models, we synthetized the waveforms for the 30 selected stations near the source region. The comparison of the synthetic waveforms with the observed records indicated that they agreed very well with each other, especially for the part of high-frequency larger than 1 Hz. We found that there were two obvious SMGAs on the fault, which take the position that the asperities from far-field seismic inversion take. The combined SMGAs we obtained were smaller than those predicted by extension of the scaling law by Somervilleetal.

strong ground motion; LushanMS7.0 earthquake; empirical Green’s function method; source parameter; waveform comparison

10.11939/jass.2015.04.007.

国家自然科学基金项目（41274068）和中国科学院、 国家外国专家局创新团队国际合作伙伴计划（KZZD-EW-TZ-19）联合资助.

2014-09-13收到初稿， 2015-03-10决定采用修改稿.

e-mail: wenbo@ucas.ac.cn

4.007

P315.01

A

药晓东， 章文波. 2015. 2013年四川芦山MS7.0地震强地面运动模拟. 地震学报, 37（4）: 599--616.

Yao X D, Zhang W B. 2015. Strong ground motion simulation for the 2013MS7.0 Lushan, China, earthquake.ActaSeismologicaSinica, 37（4）: 599--616.

doi:10.11939/jass.2015.04.007.