基于压缩感知的图像重构GUI系统

吕 军，陈 烁，李秀梅

（杭州师范大学信息科学与工程学院，浙江 杭州311121）

0 引言

传统采样中，依据Nyquist采样定理，采样频率不能低于信号最高频率的两倍.随着人们对信息需求量的增加，携带信息的信号带宽越来越宽，以此为基础的信号处理框架对采样速率、传输速度和存储空间的要求也越来越高.

压缩感知［1-3］通过远低于Nyquist采样率的方式对稀疏的或可压缩的信号进行采样，同时能以高概率精确恢复出原信号.该理论突破了Nyquist采样定理的限制，在信息论、图像处理、医疗成像、模式识别等很多领域受到广泛关注［4］.

压缩感知把自然信号经过变换基转化为稀疏信号，经过测量矩阵获得测量值，在重构算法下重建原始信号.即当信号在某个变换域上是稀疏的或可压缩的，就可以用一个与变换基不相关的测量矩阵将变换所得的高维信号投影到一个低维空间上，然后利用信号的稀疏先验信息，通过一定的线性或非线性的重构算法，从这些少量的投影中精确或近似精确地重构出原始信号.

文章利用Matlab构建了基于压缩感知的图像重构GUI系统，采用两种稀疏变换基（即小波变换基和离散余弦变换基）、四种测量矩阵（即高斯矩阵、贝努利矩阵、哈达玛矩阵和托普利兹矩阵）、两种重构算法（即正交匹配追踪算法和压缩采样匹配追踪算法）的不同组合对图像进行重构，并利用峰值信噪比PSNR作为指标，分析比较各种组合的重建性能.

1 图像的采样和重构的过程简介

压缩感知理论［2-3］主要包括三个部分：信号的稀疏表示，测量编码和重构算法.

1.1 信号的稀疏表示

当一个信号只有少量的元素是非零的，则该信号是稀疏的.但现实生活中，很多信号不是稀疏的，需要将其进行稀疏表示.信号的稀疏表示是将信号投影到变换基上，使投影后的变换系数绝大部分是很小或接近于零，从而满足稀疏性.常用的变换基有离散余弦变换基和小波变换基［3，5］.

根据调和分析理论［6-7］，一个长度为N的一维离散时间信号f，可以表示为一组标准正交基的线性组合

其中，Ψ＝［Ψ1｜Ψ2｜…｜ΨN］是N×N的变换基，N×1的列向量x是f在Ψ变换基上的变换向量，x可等价表示信号f.如果x中只有K个元素是非零的，那么就称x是K稀疏的.

1.2 测量编码

已知某一个测量矩阵Φ∈R M×N（M≪N）以及某未知信号f在该矩阵下的线性测量值y∈R M×1，即［8］

其中f是原始信号，x是f的稀疏表示，Θ＝ΦΨ称为M×N的信息算子，y是稀疏信号x关于Θ的测量值，如图1所示.坎迪斯等人指出，若要精确地重构出K稀疏信号x，测量的次数M必须满足M＝O（Kln（N）），测量矩阵Θ和变换基Ψ必须满足约束等距性条件.

图1 利用测量矩阵对信号进行压缩采样示意图Fig.1 Schematic diagram of using measurement matrix to sample the signal with compressive sensing

目前常用的测量矩阵主要分成随机矩阵和确定性矩阵［5］，随机矩阵主要有高斯矩阵、贝努利矩阵等，确定性矩阵主要有哈达玛矩阵、托普利兹矩阵等.两类测量矩阵各有优缺点：随机矩阵重建性能较好，但不易于硬件实现；确定性矩阵因为其占用的存储空间少，易于硬件实现，是未来测量矩阵的主要研究方向，普遍来说确定性矩阵的重建精度没有随机矩阵高.

1.3 重构算法

利用重构算法求解最小L0范数优化问题：

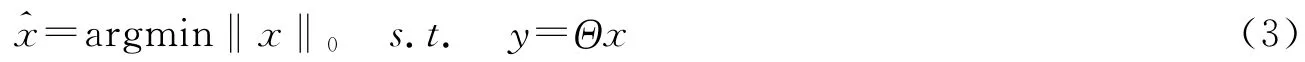
得到稀疏信号x的精确或近似重构，进而重构原始信号.最小L0范数优化问题是N-P hard问题，其主要近似求解方法有凸松弛法如基追踪算法等，和贪婪追踪算法如匹配追踪算法等［6-8］.本文主要介绍正交匹配追踪算法和压缩采样匹配追踪算法.

1.3.1 正交匹配追踪算法

匹配追踪算法是一种贪婪迭代算法，其基本思路如下：在每一次的迭代过程中从过完备原子库（测量矩阵）中选择与信号最匹配的原子来构建稀疏逼近，并且求出信号表示残差，然后再继续选择与信号残差最为匹配的原子，经过一定次数的迭代，信号可以由一些原子线性表示.由于信号在已选定原子（测量矩阵的列向量）集合上投影的非正交性使每次迭代的结果可能是次最优的，为获得收敛可能需要较多次数的迭代.正交匹配追踪算法（OMP算法）基本上克服这个问题而且继承了MP算法中的原子选择准则，通过递归地对已选择原子集合进行正交化保证迭代的最优性，减少了迭代次数.对K稀疏N维离散时间信号x，用一个M×N的高斯矩阵测量时，只需M＝O（Kln（N））.

匹配追踪算法通过求余量r与测量矩阵Φ中各个原子之间内积的绝对值，来计算相关系数u：

并采用最小二乘法进行信号逼近以及余量更新：

OMP算法的具体步骤如下：

①初始余量r0＝Y，迭代次数n＝1，索引值集合Λ＝∅，J＝∅；

②计算相关系数u，并将u中最大值对应的索引值存入J中；

③更新支撑集ΦΛ，其中ΦΛ∪J0；

④应用式（6）得到，同时用式（7）对余量进行更新；

⑤若‖rnew-r‖≥ε2，令r＝rnew，n＝n＋1转步骤②；否则，停止迭代.

1.3.2 压缩采样匹配追踪算法

OMP算法保证了每次迭代的最优性，减少了迭代的次数.但在每次迭代中仅选取一个原子来更新原子集合，这样必然会付出巨大的重建时间代价.因此出现了许多改进的匹配追踪算法，如压缩采样匹配追踪算法（CoSa MP算法），在重建时间和重建质量之间取得一个较好的平衡，保证重建质量的同时提高重建效率.

OMP算法每次只选择一个与余量相关的原子，从原子的选择方式上看实现了单个原子的精确选择.而引入回溯思想的压缩采样匹配追踪（CoSa MP）算法是从原子库中选择多个较相关的原子同时剔除部分原子，从而提高算法效率.CoSa MP算法保证了候选集合最多不会超过3K个原子，每次迭代支撑集拥有2K个原子，同时剔除的原子数目最多不超过K个.CoSaMP算法具体算法如下：

①初始余量r0＝Y，估计信号稀疏度为K，迭代次数n＝1，索引值集合Λ＝∅，J＝∅；

②用式（5）计算相关系数u，并从u中寻找2K个最大值对应的索引值存入J中；

③Λ∪J，应用式（6）得到＾Z，取前K个最大元素对应的原子放入支撑集ΦΛ；

④应用式（6）得到＾X，同时用式（7）对余量进行更新；

⑤若｜Λ｜≥2K，则停止迭代；否则令r＝rnew，n＝n＋1转步骤②.

CoSa MP算法每次迭代中都要同时选中多个原子，而且最终用于重建的支撑集大小是确定的，这就需要在迭代过程中不断选中原子的同时剔除一部分以前选中的原子.那么这种方式能否保证每轮迭代中至少选中一个最终用于信号重建的原子而不会被剔除，这是一个值得质疑的问题.研究证明即便剔除了己经选定的部分原子依然可以保证留下的原子是最优的从而精确重建信号［8］.

2 基于Matlab图像的压缩感知实现系统设计

MATLAB 是由Math Works公司开发的高级技术计算语言和交互式环境，广泛应用于算法开发、数据可视化、数据分析以及数值计算等领域.Matlab中图形用户界面GUI由窗口、光标、按键、菜单和文本等对象（Object）构成，可以通过编程控制各个控件之间协调工作.

本文将在Matlab开发环境下，完成基于压缩感知的图像重构GUI可视化系统，包括界面设计和算法程序设计.利用该GUI可视化系统，用户只需选择所需处理的图像，并选择相应的变换基、重构的域、测量矩阵、重构算法，即可以完成图像重构，并得到相应重构图像的峰值信噪比.

2.1 系统框图及说明

系统的框架如图2所示：

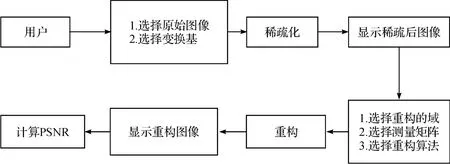
图2 系统框架图Fig.2 The system diagram

系统对应的GUI界面如图3：

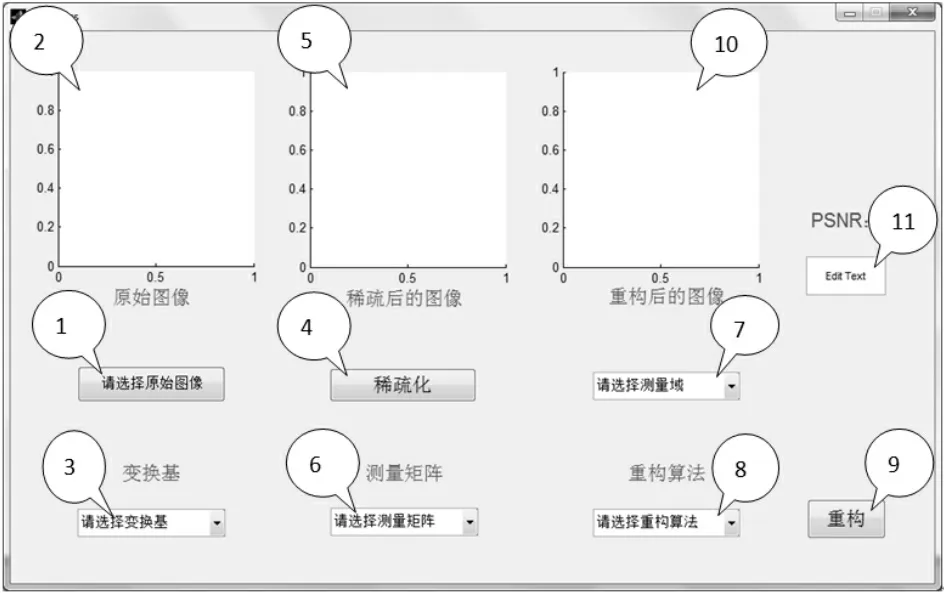
图3 系统GUI界面Fig.3 The GUI of the system

2.2 图像重构GUI系统演示

为了评价图像重构的性能，采用峰值信噪比PSNR 作为评价标准，其定义式为：

需要说明的是，采用测量矩阵对图像的系数进行采样时，可以在空间域中进行采样即针对空间的图像进行采样，也可以在变换域即经过变换基变换后的小波变换域或DCT 变换域进行采样.

下面以变换基选择小波变换基、测量矩阵选择高斯随机矩阵、重构算法选择正交匹配追踪算法OMP为例，在小波变换变换域中利用测量矩阵对样本点进行测量，进而完成图像重构.如图4所示，点击“选择原始图像”按钮，选择lena.jpg图像并显示在原始图像框中，选择“变换基”下拉菜单中的小波变换基，点击“稀疏化”按钮，显示稀疏化后的图像，再选择“选择重构域”下拉菜单中的“变换域”，选择“高斯随机矩阵”，再选择“正交匹配追踪算法”，点击“重构”按钮，完成图像的重构并显示，并在PSNR 显示框中显示计算的PSNR值.图5则显示了变换基选择小波变换基、测量矩阵选择哈达玛矩阵、重构算法选择压缩采样匹配追踪算法CoSa MP时在变换域上进行测量后所获得的重构图像GUI系统.

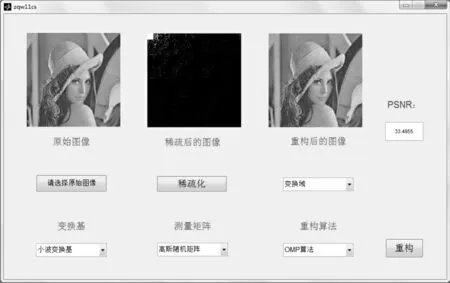
图4 利用小波变换基、高斯随机矩阵、正交匹配追踪算法OMP的图像重构结果Fig.4 The image reconstruction result with wavelet transform basis，Gaussian random matrix and OMP algorithm

图5 利用小波变换基、哈达玛矩阵、压缩采样匹配追踪算法CoSa MP的图像重构结果Fig.5 The image reconstruction result with wavelet transform basis，Hadamard matrix and CoSaMP algorithm

同样，利用该系统可以针对图像实现在小波变换基和离散余弦变换基下的稀疏化，再在空间域或者变换域上选择不同的观测矩阵和不同的重构算法实现图像的重构演示.各种不同组合情况下所得到的实验结果如表1-表4所示，其中表1为采用随机矩阵时在变换域中进行测量的重构效果，表2为采用随机矩阵时在空间域中进行测量的重构效果.从表1和表2中可以看出：在小波变换基和离散余弦变换基下，OMP重构算法的性能都优于CoSa MP重构算法的性能；当采用同一重构算法时，采用高斯随机矩阵和贝努利矩阵作为测量矩阵可以得到相近的图像重构性能；当采用同一重构算法和测量矩阵时，在变换域进行测量和在空间域进行测量，可以得到相近的图像重构性能；在其他条件相同的情况下，基于小波变换基的图像重构效果要优于在离散余弦变换基的重构效果.

其中表3为采用确定矩阵时在变换域中进行测量的重构效果，表4为采用确定矩阵时在空间域中进行测量的重构效果.从表3和表4中可以看出：当采用确定矩阵时，在小波变换基和离散余弦变换基下，在变换域进行测量的重构效果都要好于在空间域中进行测量的重构效果，原因在于利用确定矩阵从空间域进行测量时无法保证所选样本的随机性，当有些非零的系数没有被测量到时，对最终的重构效果影响比较大；在小波变换基下，在变换域进行测量时，采用托普利兹矩阵得到的重构效果要略好于采用哈达玛矩阵的效果.此外，图像经过变换基后得到的变换域稀疏，有时并不是理想的稀疏，需要进行加阈值处理，得到稀疏系数，然后再进行重构.

对比表1，表2以及表3，表4还可以看出，在相同的变换基下，采用确定矩阵在变换域上进行测量时，采用COSAMP算法重构的效果比随机矩阵好.在其它条件下，随机矩阵测量得到的重构效果普遍好于确定矩阵测量得到的重构效果.

需要说明的是，本论文中图表是以lena.jpg图像为例进行分析的，当采用不同图像时，图表结果可能会有细微区别.

表1 采用随机矩阵在变换域中进行测量的重构效果Tab.1 The reconstruction performance with random matrices in the transform domain

表2 采用随机矩阵在空间域中进行测量的重构效果Tab.2 The reconstruction performance with random matrices in the spatial domain

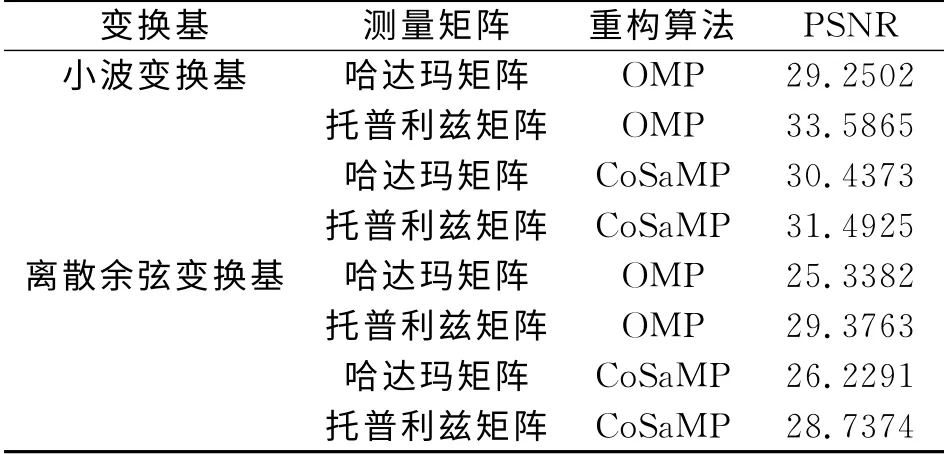
表3 采用确定矩阵在变换域中进行测量的重构效果Tab.3 The reconstruction performance with deterministic matrices in the transform domain

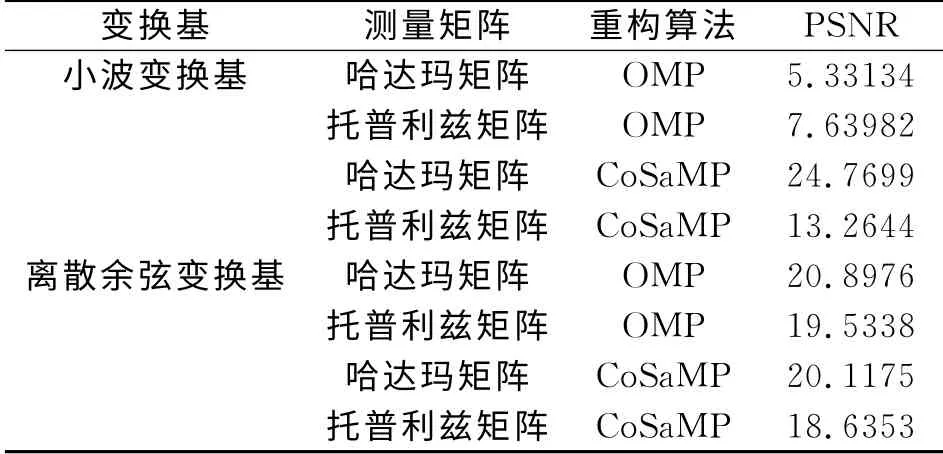
表4 采用确定矩阵在空间域中进行测量的重构效果Tab.4 The reconstruction performance with deterministic matrices in the spatial domain

3 结论

本文利用Matlab设计了基于压缩感知的图像重构GUI可视化系统，针对不同的变换基、不同的观测矩阵和不同重构算法下重构效果进行直观对比.该GUI系统作为压缩感知的实现平台，能够直观分析图像在不同条件下基于压缩感知方法进行重构的效果以及更好地理解压缩感知的过程.从结果分析可以看出，利用随机矩阵进行测量得到的重构效果要好于利用确定矩阵进行测量得到的重构效果；利用确定矩阵在空间域上进行测量所得到的重构效果较差，不能完成较好的图像重构；基于小波变换基，利用随机矩阵在变换域上进行测量，并利用OMP算法进行重构的效果最好.鉴于随机矩阵不易于硬件实现，为了便于硬件实现且保证较好的图像重构性能，可以利用确定矩阵，基于小波变换基在变换域上利用OMP算法进行图像重构.

［1］Candes E，Romberg J，Tao T.Robust uncertainty principles：Exact signal reconstruction from highly incomplete frequency information［J］.IEEE Transaction on Information Theory，2006，52（2）：489-509.

［2］邵文泽，韦志辉.压缩感知基本理论：回顾与展望［J］.中国图像图形学报，2010，17（1）：1-12.

［3］尹宏鹏，刘兆栋，柴毅，等.压缩感知综述［J］.自动化学报，2013，28（10）：1441-1445.

［4］侯金曼，何宁，吕科.基于压缩感知的图像快速重建方法［J］.计算机工程，2011，37（19）：215-217.

［5］焦李成，杨淑媛，刘芳，等.压缩感知回顾与展望［J］.电子学报，2011，39（7）：1651-1658.

［6］Baraniuk R G.Compressive Sensing［J］.IEEE Signal Processing Magazine，2007，24（4）：118-121.

［7］Emamnuel J，Candes E，Michael B W.An Introduction to Compressive Sampling［J］.IEEE Signal Processing Magazine，2008，25（2）：21-30.

［8］赵玉朗.压缩传感在信号采集系统中的应用研究［D］.天津：南开大学，2010.