异常空心光束在梯度折射率介质中的传输特性

沈 琦，王奎龙

（杭州师范大学理学院，浙江 杭州310036）

0 引言

由于折射率的横向变化对光束将产生波导效应以及类透镜效应，非均匀折射率介质在光通信、光传感技术和光纤熔接等领域具有广阔的应用前景［1-4］.在非均匀折射率介质中，梯度折射率介质的特性及其应用得到了广泛的研究.高斯光束、余弦高斯光束、平顶光束、可控空心光束及洛伦兹-高斯光束在梯度折射率介质中的传输已得到了研究.近年来，一类被称为空心光束的中心光强为零的暗中空心光束，由于在原子光学、自由光通信、二元光学、中性原子的激光操控和导向等方面的广泛应用而受到人们的广泛关注［5-8］.在理论和实验上，有多种不同的模型和方法可用来描述和产生空心光束，如拉盖尔-高斯模、贝塞耳-高斯光束、高阶马丢光束等.2005年，Wu等在实验中发现了一种新颖的椭圆对称的异常空心光束［9］.异常空心光束与传统空心光束最大不同是其中心带有椭圆形的实心核.随后Cai提出了描述该光束的理论模型，把异常空心光束看作像散高斯模型和像散圆环模型的叠加［10］.Cai提出模型后，异常空心光束的各种传输特性得到了较为深入的研究［11-19］，但是异常空心光束在梯度折射率中的传输特性研究还未见报道.本文利用广义惠更斯-菲涅耳衍射（Collins）积分方法，推导出异常空心光束在梯度折射率介质中的传输解析表达式，并研究了异常空心光束在梯度折射率介质中及穿过介质后的传输特性.

1 异常空心光束在梯度折射率径向分布介质中的传输公式

在直角坐标系中，z轴为光束传播方向.在初始平面（z＝0）处，异常空心光束的电场分布可以描述为：

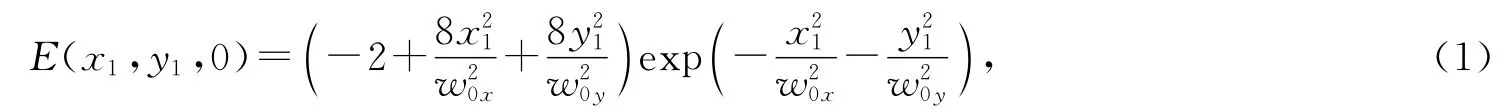
式中，w0x和w0y分别表示像散高斯光束在x和y方向的束腰宽度.

在近轴条件下，异常空心光束通过一阶ABCD光学系统后出射场的分布可由直角坐标下的Collins积分公式得到

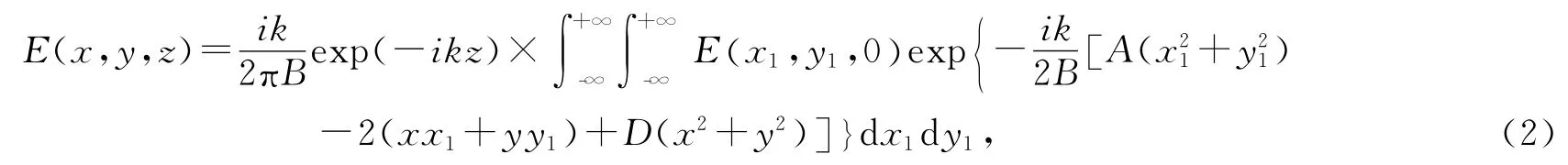
其中k＝2π／λ，λ为波长，A、B、C、D为一阶光学系统变换矩阵元.

把式（1）代入式（2），并使用下面的积分公式

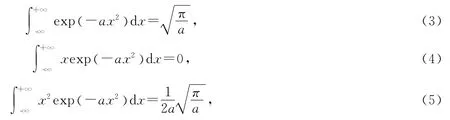
经过复杂积分运算，可得到异常空心光束经过一阶ABCD光学系统后出射场分布的表达式

假设异常空心光束通过梯度折射率径向分布的介质，其光路图和梯度折射率在径向分布情况如图1所示.

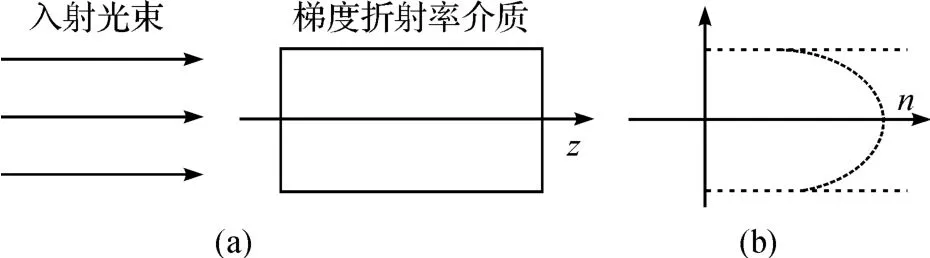
图1 异常空心光束在梯度折射率介质中的传输示意图Fig.1 Scheme of anomalous hollow beam propagation in gradient-index medium

梯度折射率径向分布介质的折射率可表示为

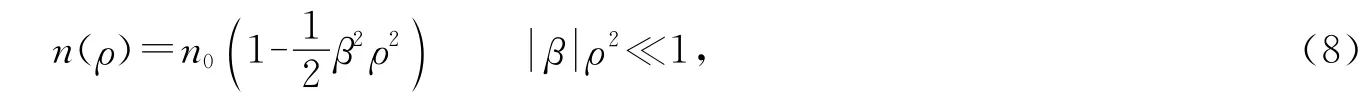
式中，n0为介质轴上的折射率，β为梯度折射率系数.梯度折射率介质中从源平面到观察平面z之间的光学系统传输矩阵可表示为

将式（9）代入式（6），可得异常空心光束在梯度径向分布的梯度折射率介质中的传输表达式

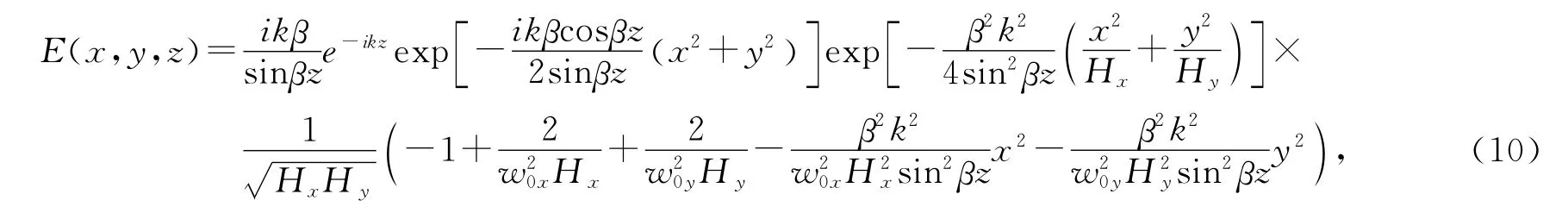
由I＝E（x，y，z）E＊（x，y，z），可得异常空心光束在梯度折射率介质中的光强分布

其中

当x＝y＝0时，由式（12）可得到异常空心光束在梯度折射率介质中的轴上光强分布为：

由式（23）可知，轴上光强分布呈周期性变化，相应的空间周期为π／β，周期由梯度折射率系数决定，而与其它因素无关，而轴上光强最大值位置为

异常空心光束在观察平面z上二阶矩定义下的有效光束宽度为［20］

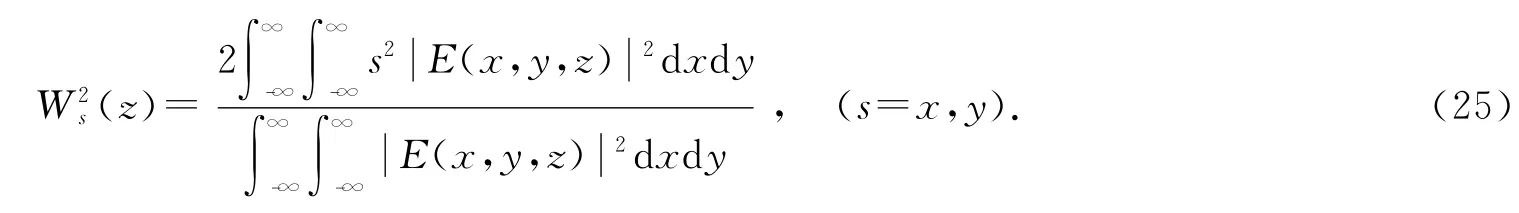
把式（10）代入式（25），通过积分可得异常空心光束在z平面上的有效光束宽度为

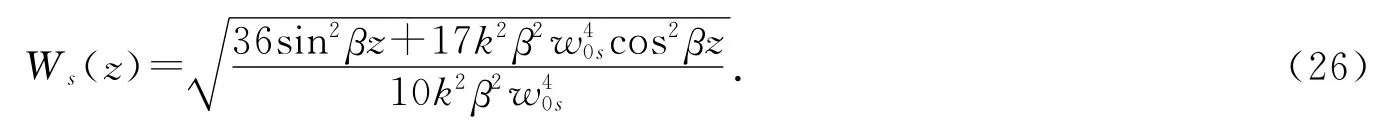
2 数值计算和分析

利用以上推导出的公式（12），（23），（26）进行数值计算，获得了异常心光束在梯度折射率介质中及介质后的传输特性，在以下的计算中，取λ＝632.8 nm，w0x＝2 mm，w0y＝1 mm.在图2中给出了异常空心光束在梯度折射率中传输时，轴上归一化光强随着传输距离的变化.从图2中可以看出，轴上光强分布呈周期性变化，轴上光强分布周期由Sin2（βz）决定，即βz＝0.5π＋nπ（n＝0，1，2，…）时，轴上光强达到最大值.在轴上光强最大值两侧，轴上光强从最大值快速下降，但下降的快慢与β值有关，β值越大，轴上光强下降得越快.图3所示为当β＝0.5mm-1时，在不同传输距离处的横向归一化光强的三维分布和等高分布图.从图3可以看出，在两个相邻的轴上光强最大值空间范围内，随着传输距离的变化，光束横向分布剖面形状将发生变化，光束横向分布范围先逐渐增大，再逐渐减小，而中心光强先逐渐减小再逐渐增大，同时，椭圆对称的异常空心光束的对称性也发生变化，并随着传输距离的变化，椭圆光束的x和y方向的长短轴会发生交换，其光束形状在一个周期内的变化过程类似于自由空间的传输变化，但变化速度远快于自由空间的传输，并且具有周期变化的特性.

图2 梯度折射率系数取不同值时轴上归一化光强随传输距离的变化Fig.2 Normalized intensity on axis changes with propagation distance for different gradient-index parameters

图3 不同传输距离处横向归一化光强分布图（β＝0.5 mm-1）Fig.3 Normalized intensity distributions with different propagation distances（β＝0.5 mm-1）

图4给出了在z＝πmm 处，当梯度折射率系数取不同值时，横向归一化光强的三维分布和等高分布图.从图4可以看出，在同一传输距离处，当梯度折射率系数取不同值时，光束的分布形状将发生类似于改变传输距离的变化情况，即会发生周期性的变化.当z＝πmm，β从0.1增加到0.9时，光束的横向分布范围先逐渐变小，再逐渐增大，光束的形状也发生变化，光束形状的变化周期为β＝0.5＋n（n＝0，1，2，…）.

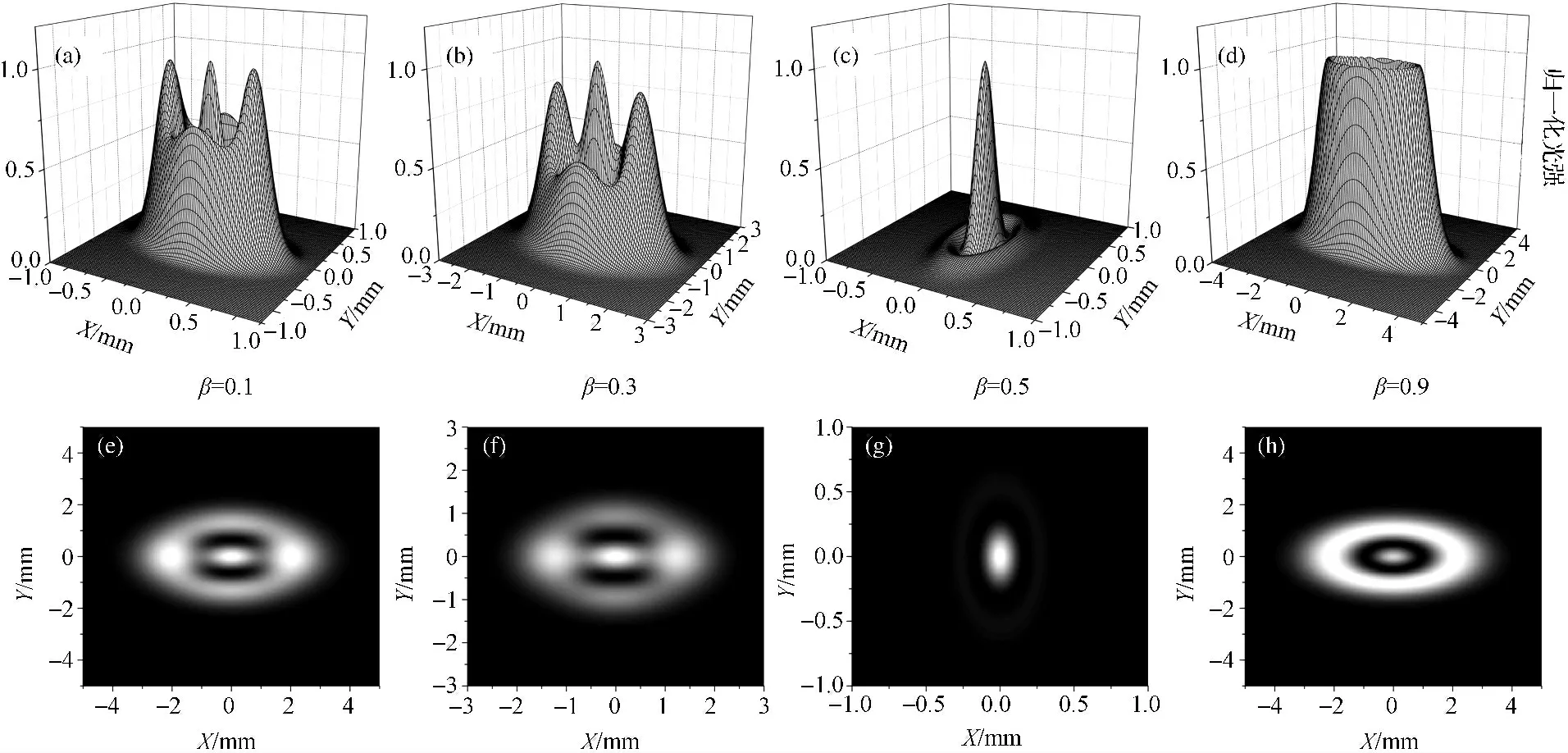
图4 不同梯度折射率时横向归一化光强分布（z＝πmm）Fig.4 Normalized intensity distribution with different gradient-index parameters（z＝πmm）

如果式（9）中的矩阵元变为A′＝A＋z0C，B′＝B＋z0D，C′＝C和D′＝D，则可以研究异常空心光束通过梯度折射后在自由空间的传输特性，其中A、B、C和D为式（9）中矩阵元值，z0为梯度折射率后自由空间的传输距离.通过数值模拟发现，通过梯度折射率介质后的传输特性与文献［10］中描述的类似，光束横向光强的归一化分布与介质的厚度，β参数，以及自由空间的传输距离有关，实际中可以通过改变介质的厚度与β参数来调控自由空间某一传输面上的光束分布.由于篇幅所限，图5仅给出了当光束通过厚度为z＝πmm，而β值不同的梯度折射率介质后，距离介质z0＝1 m 处的横向归一化光强分布，从图5中可以看出，当光束通过不同β值的梯度折射率介质后，在介质后自由空间1 m 处可以获得不同的光束形状和光强分布.

图5 梯度折射率介质后自由空间的横向归一化光强分布（z＝πmm，z0＝1m）Fig.5 Normalized intensity distribution in free space after passing through the gradient-index medium（z＝πmm，z0＝1m）

在图6中给出了，有效光束宽度随着传输距离的变化图，图中给出了当β分别取0.5和1时，x方向和y方向有效光束宽度随传输距离的变化.从图6中可以看出，x和y方向的有效束宽变化规律是一样的，都呈周期性的变化，其变化空间周期为π／β，在一个周期内，其中前半个周期有效束宽从最大值逐渐减小到零，后半个周期从零逐渐增大到最大值.从图6（a）和图6（b）比较可以看出，当增大梯度折射率系数时，有效束宽变化范围得到压缩.

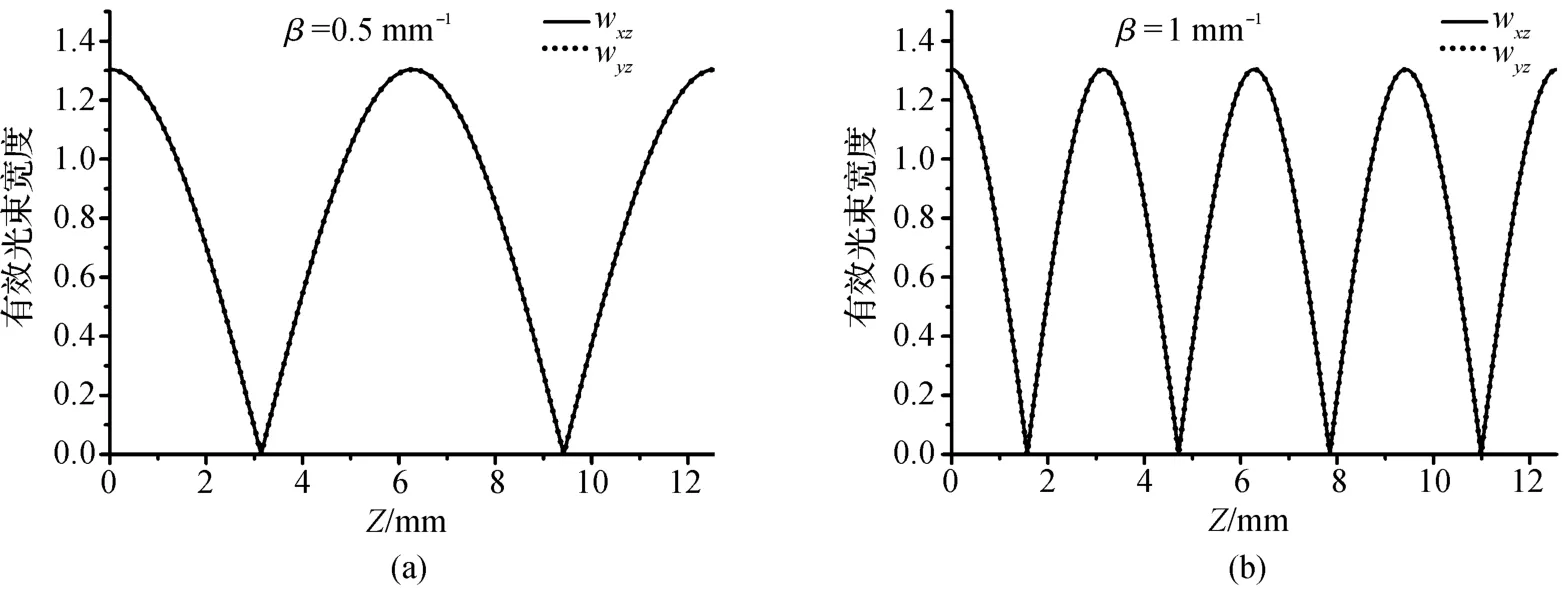
图6 梯度折射率系数取不同值时光束宽度随传输距离的变化Fig.6 Beam width changes with propagation distance for different gradient-index parameters

3 结论

本文根据柯林斯积分公式导出了异常空心光束在梯度折射率介质中传输的解析公式，并给出了梯度折射率介质中观察平面上二阶矩定义下的光束宽度变化表达式.通过数值计算分析了异常空心光束在梯度折射率介质中及穿过介质后的传输规律.计算结果表明，在梯度折射率介质中，异常空心光束的轴上光强分布和有效光束宽度都呈周期性变化，折射率系数越大，轴上光强变化速率越快.异常空心光束在梯度折射率介质中的横向光强分布受折射率影响很大，当轴向传输距离或折射率系数变化时，光束的横向光强分布呈周期性的变化，而穿过介质后在自由空间的传输受介质和传输距离的影响.本文的研究结果对异常空心光束在梯度折射率介质中及穿过介质后传输的光强和光束形状控制提供了有意义的参考，可以通过改变传输距离和梯度折射率系数来调整光束的强度和形状，对光束形状有特殊要求场合及光束整形具有潜在的应用价值.

［1］Sobert J H，Kimberly-clark C，Neenah W I，etal.Web inspection using gradient-indexed optics［J］.IEEE，2005，41（6）：295-299.

［2］Ballav M，Chowdhury A R.A generlized nonlinear Schöodinger equation and optical soliton in a gradient index cylindrical media［J］.Chaos，Solitons ＆Fractals，2007，31（4）：794-803.

［3］Yablon A D，Bise R T.Low-loss high-srengh microstructured fiber fusion splices using GRIN fiber lense［J］.IEEE，2005，17（1）：118-120.

［4］Siegman A E.Lasers［M］.Calicornia：University Science Book，1986：586-589.

［5］Yin J P，Gao W J，Zhu Y F.etal.Generation of dark hollow beams and their applications in laser cooling of atoms and all optical-type bose-einstein condensation［J］.Chinese physics，2002，11（11）：1157.

［6］Kuga T，Torii Y，Shiokawa N，etal.Novel optical trap of atoms with a doughnut beam［J］.Phys Rev Lett，1997，78（25）：4713-4716.

［7］Ito H，Nakata T，Sakaki K，etal.Laser spectroscopy of atoms guided by evanescent waves in micron-sized hollow optical fibers［J］.Phys Rev Lett，1996，76（24）：4500-4503.

［8］Yin J P，Zhu Y F，Jhe W，etal.Atom guiding and cooling in a dark hollow laser beam［J］.Phys Rev A，1998，58（1）：509-513.

［9］Wu Y K，Li J，Wu J.Anomalous hollow electron beams in a storage ring［J］.Phys Rev Lett，2005，94（13）：134802.

［10］Cai Y J.Model for an anomalous hollow beam and its paraxial propagation［J］.Opt Lett，2007，32（21）：3179-3181.

［11］Wang K L，Zhao C L，Xu B J.Propagation of anomalous hollow beam through a misaligned first-order optical system［J］.Opt Laser Technol，2010，42（8）：1218-1222.

［12］Wang K L，Zhao C L.Fractional Fourier transform for an anomalous hollow beam［J］.J Opt Soc Am A，2009，26（12）：2571-2576.

［13］Wang，K L，Zhao C L.Analytical solution for an anomalous hollow beam in a fractional Fourier transforming optical system with a hard aperture［J］.Opt Laser Technol，2012，44（5）：1232-1239.

［14］Wang K L，Zhao C L.Propagation properties of a radial phased-locked partially coherent anomalous hollow beam array in turbulent atmosphere［J］.Opt Laser Technol，2014，57：44-51.

［15］Wang K L，Zhao C L.Nonparaxial propagation of a vectorial apertured off-axis anomalous hollow beam［J］.Opt Commun，2015，334：280-286.

［16］Cai Y J，Eyyubo？lu H T，Baykal Y.Propagation properties of anomalous hollow beams in a turbulent atmosphere［J］.Opt Commun，2008，281（21）：5291-5297.

［17］Cai Y J，Wang F.Partially coherent anomalous hollow beam and its paraxial propagation［J］.Phys Lett A，2008，372（25）：4654-4660.

［18］王奎龙.异常空心光束通过环形光阑的传输特性［J］.杭州师范大学学报：自然科学版，2010，9（6）：468-472.

［19］王奎龙，异常空心光束通过硬边光阑失调光学系统的传输［J］.杭州师范大学学报：自然科学版，2014，13（1）：63-67.

［20］Carter W H.Spot size and divergence for Hermite Gaussian beams of any order［J］.Applied optics，1980，19（7）：1027-1029.