基于欧拉指数方法的活化计算程序开发及应用
韩文静,陈义学,张竞宇,彭 奕
(1.华北电力大学 核科学与工程学院,北京 102206;2.国家核电技术有限公司 北京软件技术中心,北京 100029)
核反应堆运行中会产生大量中子,这些中子对结构部件、冷却回路中的腐蚀产物有很强的活化作用,所形成的活化产物是核反应堆运行和检修人员职业照射的主要来源,因此材料的中子活化计算对于核反应堆屏蔽设计、辐射防护具有重要意义。
燃料元件包壳材料是核反应堆的核心材料之一,燃料元件的使用寿命和安全可靠性与包壳材料的性能密切相关[1]。包壳材料是核反应堆安全的第一道屏障,主要用于包容裂变产物、阻止裂变产物外泄,同时为燃料和冷却剂提供隔离屏障,避免燃料与冷却剂发生反应。包壳材料应综合考虑中子吸收截面、抗辐照损伤能力、抗腐蚀性能、强度、塑性及蠕变性能等方面进行选取。锆合金由于具有中子吸收截面低、抗腐蚀性能和力学性能优良等被广泛用作燃料元件包壳以及其他堆内部件的结构材料。随着核反应堆向高燃耗和长循环燃料周期方向的发展,对燃料元件包壳材料的性能不断提出更高的要求[2]。为适应这些要求,各国在第二代低锡Zr-4合金的基础上研究开发新型锆合金,包括已得到工程应用的ZIRLO、M5 和E635,以及我国研制的具有应用前景的Zr-Sn-Nb系列的N18新锆合金。
本文主要基于欧拉指数方法自主开发核反应堆材料的中子活化计算程序EuACT,计算Zr-4、ZIRLO、M5和N18等4种主要燃料元件包壳材料在不同辐照历史下的放射性比活度以及衰变余热随停堆时间的变化,并与欧洲先进活化程序FISPACT 的计算结果进行对比。
1 理论模型
1.1 活化模型
活化问题主要研究在核反应堆堆芯区域的材料活化。当材料处于强中子场环境,会带来诸如材料活化、辐照损伤等问题,这些问题大部分都直接或间接与中子有关,本文着重关注中子对材料的活化计算。活化计算的关键是活化材料的核子密度随辐照历史的变化,进而求得相应的比活度变化和衰变余热变化情况。对于材料中的任一核素,都可建立核素的核子密度随时间变化的方程,即:
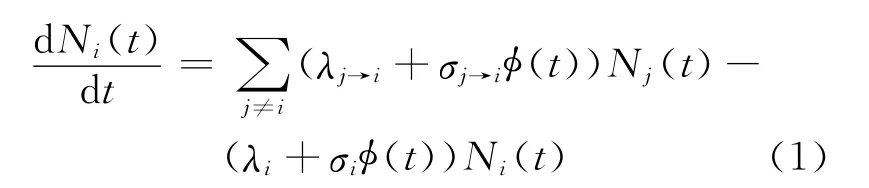
其中:Ni为第i种核素的核子密度,m-3;λj→i为第j种核素衰变为第i种核素的衰变分支比;λi为第i种核素的衰变常量,s-1;σi为第i种核素的微观反应截面,cm2;σj→i为第j 种核素活化为第i种核素的微观反应截面,cm2;φ为中子注量率,cm-2·s-1。
通常,求解活化方程的方法分为解析方法和数值方法两类。解析方法整体计算精度较高,但需对核素的反应链进行线性化处理,在线性化过程中不可避免会引入截断误差,且当核素数量、反应类型较多时,将核素的反应链线性化处理的过程较复杂。数值方法不需对核素的反应链进行提前处理,大幅降低了研究人员的工作量,且在时间步选取恰当的情况下,可接近解析方法的计算精度,所以本文选取数值方法进行计算。常用的数值方法包括欧拉指数方法、龙格-库塔法、矩阵指数法、帕德近似法[3]、切比雪夫有理近似方法[4]等。
1.2 欧拉指数方法
欧拉指数方法是基于有限差分的数值方法,在欧拉方法的基础上对时间项进行指数形式的展开,以增加欧拉方法的求解稳定性,如式(2)所示。欧拉指数方法已在材料活化计算领域得到应用,实践表明其具有较高的计算精度和计算速度[5],因此本文选取该方法求解活化方程。
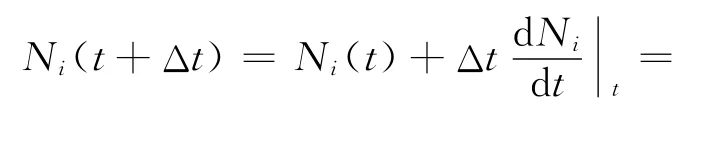

其中:t为当前计算的活化时间;Δt为单步计算步长;Λi=λi+σiφ。
欧拉指数方法在对时间项进行指数形式的展开时,需将时间步长与最大特征值的倒数相关联,因此,需考虑最大特征值的限制,这在物理上意味着所计算的核素必须具有足够大的半衰期。其他的短寿命核素则被认为处于平衡状态,可用式(3)来近似求解短寿命核素的核子密度。
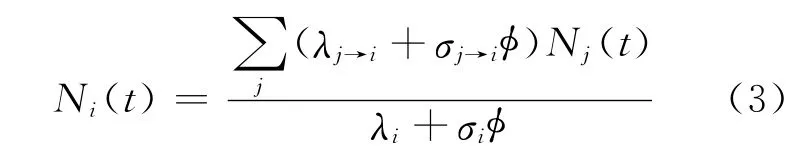
1.3 活化计算程序开发
EuACT 程序在开发过程中,除了采用欧拉指数方法求解活化方程,还使用了欧洲先进活化程序FISPACT-2007配套的数据库EAF-2007。该数据库包括了活化计算所需的全部核数据,即中子诱发反应的截面、氘核诱发反应的截面、质子诱发反应的截面以及衰变数据等。EuACT 程序结构如图1所示。
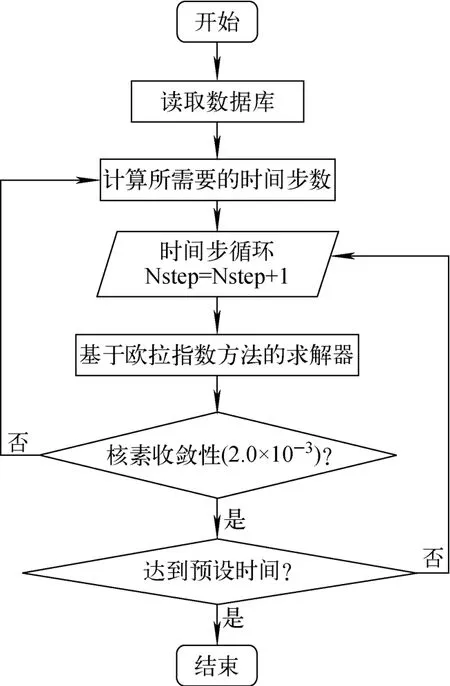
图1 EuACT 程序结构Fig.1 Structure of EuACT code
程序首先对核素进行核子密度计算,其次检验所有核素的收敛性,程序中默认设置收敛精度为2.0×10-3。如果有核素未收敛,则将时间步长数目加倍,重复上述步骤,直至达到预设的精度。为保证计算效率,程序会设置最大循环的时间步数(step),如果当前循环步数(Nstep)达到最大循环的时间步数仍未达到预设的计算精度,则强制进行计算。
2 计算结果分析
在燃料元件包壳材料的选取标准中,除对其氢化特性、腐蚀特性、蠕变特性以及辐照性能等提出要求外,包壳材料及其杂质成分的活化水平分析在反应堆设计与评价中是非常必要的[2]。本文选取常用于包壳材料的4种锆合金进行活化计算,其元素成分列于表1。

表1 4种包壳材料的元素组成Table 1 Elements in four kinds of cladding materials
2.1 比活度
图2为不同辐照历史下Zr-4比活度随停堆时间的变化。可见,EuACT 程序与FISPACT 程序的计算结果吻合较好。在3种辐照历史下,Zr-4比活度随停堆时间的变化趋势基本一致,区别在于辐照时间增加后,比活度也略有增加。其余3种包壳材料的计算结果也呈现出相似的规律。
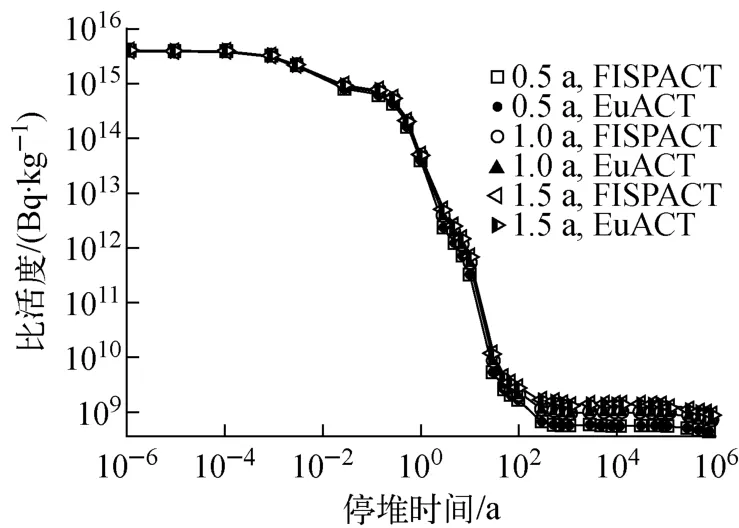
图2 Zr-4包壳材料的比活度Fig.2 Specific activity of cladding material Zr-4
图3为4种包壳材料辐照1.5a后比活度随停堆时间的变化。可见,Zr-4、ZIRLO、M5、N18等4 种包壳材料在停堆初期比活度约为1015Bq/kg,变化较平缓,在停堆200d后,比活度下降1 个量级。Zr-4 比活度在停堆初期主要受核素95Nb、95Zr影响,60Co、125Sb和121Sn分别在后续不同时间段内占主导地位。停堆1a后,Zr-4比活度开始快速下降,明显低于其余3种包壳材料,这种优势将一直保持到停堆100a左右。在停堆104a后,其余3种材料的比活度才会下降到与Zr-4相同量级。由此可知,选用Zr-4作为包壳材料在降低比活度方面有较明显的优势。
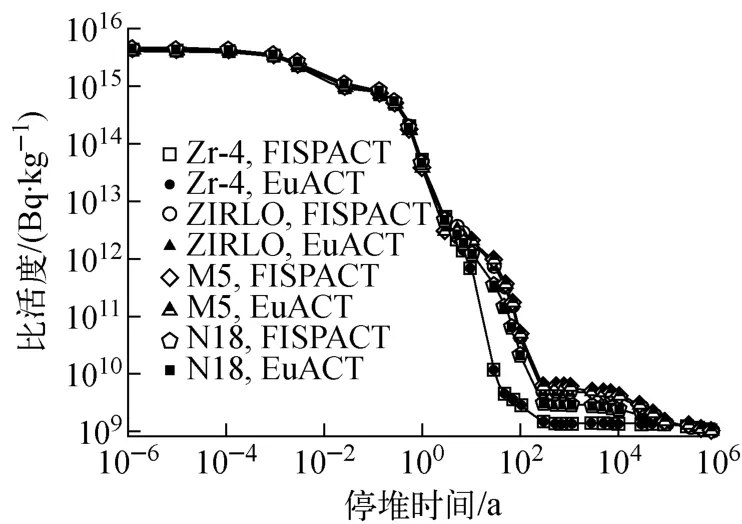
图3 4种包壳材料辐照1.5a后的比活度Fig.3 Specific activity of four kinds of cladding materials after 1.5years of irradiation
2.2 余热

图4 Zr-4包壳材料余热Fig.4 Decay heat of cladding material Zr-4
图4为Zr-4在不同辐照历史下反应余热随停堆时间的变化。可见,EuACT 程序与FISPACT 程序的计算结果吻合较好。在3种辐照历史下,Zr-4余热随停堆时间的变化趋势基本一致。其余3种包壳材料的计算结果也呈现出相似的规律。
图5为4种包壳材料辐照1.5a后其余热随停堆时间的变化。4种包壳材料在停堆初期余热约为0.60~0.75kW/kg,变化较平缓,此后余热开始迅速下降,从开始停堆到停堆1a左右,余热主要由核素95Nb 和95Zr产生,在 停堆1~10a期间,95Nb和95Zr快速衰变,不再是产生余热的主要核素,而核素125Sb对余热的贡献则越来越大。在停堆10a后,影响Zr-4余热的核素主要是125Sb(T1/2=2.75a),其余3种包壳材料因含有94Nb(T1/2=2.0×104a),所以余热下降缓慢。在停堆105a后,其余3种包壳材料的余热才会下降到与Zr-4相同量级。由此可知,选用Zr-4作为包壳材料在降低余热方面有较明显的优势。
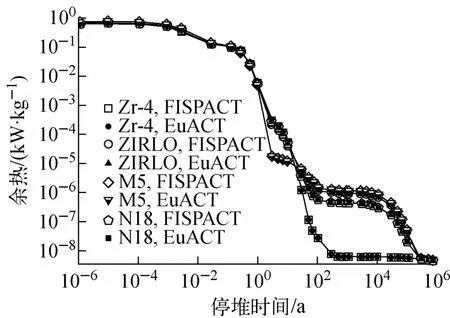
图5 4种材料辐照1.5a后的余热随停堆时间的变化Fig.5 Decay heat of four kinds of cladding materials after 1.5years of irradiation
3 结论
本文基于欧拉指数方法和EAF数据库,自主开发了活化计算程序EuACT,计算了Zr-4、ZIRLO、M5 和N18 等4 种 主 要 包 壳 材 料 在0.5、1.0和1.5a辐照历史下放射性比活度以及衰变余热随停堆时间的变化,并与欧洲先进活化程序FISPACT 的计算结果进行了对比,无论是从具体数值还是从变化趋势上,两程序计算结果吻合都非常好,初步验证了EuACT程序的可用性,后续还将采用更多例题对Eu-ACT 程序进行验证。此外,通过对4种包壳材料的活化计算结果进行对比可发现,无论在比活度还是余热方面,传统材料Zr-4都具有较为明显的优势,在短期内还无法被其他新型材料取代。当然,根据包壳材料的评价标准,还需对停堆剂量率、抗腐蚀性以及吸氢脆化等方面进行综合考虑和选择,以满足高燃耗和长循环燃料周期的要求。
[1] 邱军,赵文金.3 种锆合金的高温氧化行为[J].金属学报,2011,47(9):1 216-1 220.QIU Jun,ZHAO Wenjin.High temperature oxidation behaviour of three zirconium alloys[J].Acta Metallurgica Sinica,2011,47(9):1 216-1 220(in Chinese).
[2] 韩静茹,陈义学,袁龙军,等.C276镍基合金中子辐照活化计算分析[J].华北电力大学学报,2012,39(6):105-108.HAN Jingru,CHEN Yixue,YUAN Longjun,et al. Neutron irradiation activation calculation analysis of the C276nickel alloy[J].Journal of North China Electric Power University,2012,39(6):105-108(in Chinese).
[3] Nuclear Engineering Fundamentals.Handbook of nuclear engineering[M].USA:Springer Science Business Media,2010.
[4] PUSA M,LEPPANEN J.Solving linear systems with sparse Gaussian elimination in the Chebyshev rational approximation method[J].Nuclear Science and Engineering,2013,175:250-258.
[5] FORREST R A.FISPACT-2007:User manual[M].UK:EURATOM/UKAEA Fusion Association,Culham Science Centre,2007.

