含有控制时滞的多输入离散系统的变结构控制*
邓 臻,陈红燕,高存臣
(1.青岛工学院基础教育学院,山东 青岛 266300;2.中国海洋大学数学科学学院,山东 青岛 266100)
含有控制时滞的多输入离散系统的变结构控制*
邓 臻1,陈红燕1,高存臣2
(1.青岛工学院基础教育学院,山东 青岛 266300;2.中国海洋大学数学科学学院,山东 青岛 266100)
给出了多输入离散系统的基于时变衰减幂次趋近律的滑模变结构控制方法,并通过时滞变换将结果推广到含有控制时滞的情形。首先选取具有适当增益矩阵的线性切换函数以保证系统在切换面上的理想准滑模运动方程的极点可任意配置。其次基于时变衰减幂次趋近律设计了准滑模控制器,该控制器能够保证两类离散系统的运动轨迹在有限时间内到达准滑模带,然后要么直接转入理想准滑模,要么在准滑模带中以指数幂速率快速趋于理想准滑模,并使系统的运动轨迹能够渐近趋于状态空间的原点,而不再是原点附近某邻域中出现稳定抖振。最后的仿真结果进一步表明了这种方法的有效性。
离散系统;变结构控制;多输入;时滞;抖振

时滞的存在使离散系统的分析与综合问题变得更加复杂和困难,时滞往往是系统不稳定和性能变差的根源[10-11]。相应地,时滞离散系统的变结构控制也是现实需要解决的难题。虽然可以通过扩维技术将时滞离散系统转化为无时滞系统,但对时滞较大和/或维数较高的系统,扩维后其系统维数将按几何规律增加,而且对测量和/或控制时滞的离散系统,扩维后状态反馈控制律一般是物理不可实现的[12-14]。
本文首先将时变衰减幂次趋近律推广到了多输入离散系统,然后进一步研究了含有控制时滞的多输入离散系统的变结构控制问题。首先,可适当选取增益矩阵使系统在线性切换面上的理想准滑模运动方程可任意配置极点,其次,设计的时变衰减幂次趋近律能够保证两类离散系统的运动轨迹在有限时间内到达系统的准滑模带,并以指数幂次趋于切换面,从而最终趋于原点,而不再是原点附近的小的抖振。仿真结果表明了本文方法的有效性和优越性。
1 多输入离散系统
考虑多输入离散系统
(1)
其中:x(k)∈Rn;u(k)∈Rm分别是状态向量和控制输入向量,常数矩阵A∈Rn×n,B∈Rn×m。假设矩阵B列满秩,且(AB)完全可控。
不失一般性,假设
(2)
其中:B1∈R(n-m)×m;B2∈Rm×m,则可选取可逆线性变换将系统(1)化为简约形式[3],故不妨假设系统(1)已经是如下简约型
(3)
其中:x1(k)∈Rn-m;x2(k)∈Rm。
取线性切换函数
s(k)=Cx(k)=C1x1(k)+C2x2(k)
(4)
其中:C1∈Rm×(n-m);C2∈Rm×m为待定增益矩阵,且det(C2)≠0。
从s(k)=0中解出x2(k)代入式(3)即得理想准滑模的运动方程
(5)
由于(AB)完全可控,故(A11A12)完全可控[3],可以选择适当的增益矩阵C=[C1C2]使理想准滑模具有任意配置的极点集。下面还需要设计滑模控制器,一方面保证系统(1)对任意的初始状态其解序列能在有限时间内到达准滑模带,另一方面保证准滑模带(或切换带)的宽度足够小,且使非理想准滑模稳定。为下文需要,在此引入2个引理。
引理1[9]对于文献[8]提出的衰减幂次趋近律
(6)
其中:0 (2)任意给定初始值s(0)≠0,有 (3)sgn(s(k+1))=sgn(s(k))当且仅当 引理2[9]对于单输入离散系统,文献[9]提出了时变衰减幂次趋近律 (7) 其中:0 由引理1和2知,衰减幂次趋近律(6)并不能保证切换函数s(k)趋于切换面,其极限状态是出现稳态抖振,稳态抖振的范围是[-Δ,Δ],其中Δ=[εT/(2-qT)]1/1-a,而时变衰减幂次趋近律(7)则保证了抖振的振幅Δ以指数幂次趋于零。 针对多输入离散系统(1)与(4),提出如下的时变衰减幂次趋近律 (8) 或如下分量形式 (9) 其中常数T是采样周期,0 q=diag(q1,q1,…,qm), ε=diag(ε1,ε1,…,εm), 将时变衰减幂次趋近律(8)代入系统(1)或(3),可得如下2种形式的滑模变结构控制器(两者等价) (10) 或 (11) 将控制律(11)代回系统(3)即得滑模趋近过程的运动差分方程 (12) 注意该方程在切换面S0:s(k)=0是没有定义的。实际上,切换带内的非理想准滑模运动控制方程也是(12),但必须要求方程的定义范围是切换带 (13) 或彼此的交集区域。 由于方程(12)并不直观,取可逆线性变换 (14) 则运动方程(12)可化成如下形式[3] (15) 这正是所期待的结果形式。 对于运动差分方程(15),由引理2知,状态s(k)将于有限时间内到达切换带,并以指数幂次趋于切换面S0。而若取s(k)=0,则式(15)中的第一式即为理想准滑模的运动方程,它具有任意配置的极点集。因此,易得如下结论。 引理3 多输入离散系统(1)在线性切换函数(4)和时变衰减幂次趋近律(8)作用下,系统状态将于有限时间内到达准滑模带,并在其内以指数幂次趋于切换面(也即理想准滑模)。如果理想准滑模具有任意配置的极点集,那么系统状态将最终收敛于原点,从而消除了系统的稳态抖振。 注1 由于文献[1-3]中的离散指数趋近律和文献[8]的衰减幂次趋近律,s(k)都存在稳态抖振,因此其设计的滑模控制器只能保证系统状态稳定到原点附近某邻域Ω0内的小稳态抖振而非原点本身,其中邻域大小是 (16) 注2 可取a(k)=1-e-pk(p>0)或a(k)=1-1/k,显然前者要优于后者,当然也可以选取其他形式。 考虑多输入多控制时滞离散系统 (17) (18) 下面设计系统(17)的准滑模变结构控制器。 首先作如下时滞变换 (19) 则系统(17)的第一式变为 y1(k+1)= (20) 然后分别引入第q步时滞变换 yq(k)= (21) 一系列变换推导后得 (22) 仍取线性滑动模切换函数 s(k)=Cym(k) (23) (24) 类似的方法可以得到如下定理。 定理 多输入离散系统(17)在线性切换函数(23)和时变衰减幂次趋近律(8)作用下,系统状态将于有限时间内到达准滑动模态带,并在其内以指数幂次趋于切换面(也即理想准滑模)。如果理想准滑模具有任意配置的极点集,那么系统状态将最终收敛于原点,从而消除了系统的稳态抖振。 考虑如下多输入离散系统状态方程 x(k+1)=Ax(k)+B1u(k-2) (25) 引入时滞变换(19)式,则方程(25)变成 (26) 图1(a) 本文方法的状态轨线 图1(b) 文献[8]方法的状态轨线 图1(c) 文献[2]方法的状态轨线 图2(a) 本文方法的切换函数 图2(b) 文献[8]方法的切换函数 图2(c) 文献[2]方法的切换函数 由图1~2可以看出,文献[2]和[8]两种方法都存在稳态抖振。根据给定的算例参数可知,文献[2]方法下切换带s(k)的稳态抖振的范围是[-0.5 0.5],文献[8]方法下切换带s(k)的稳态抖振的范围是[-0.25 0.25],文献[8]改进了文献[2]的趋近律,使稳态抖振有所减小,但并没有消除稳态抖振。而本文方法下并不存在稳态抖振,抖振快速衰减并最终趋于零。因此,仿真结果表明本文方法是优越的。 本文基于时变衰减幂次趋近律,研究了多输入离散系统的变结构控制策略,通过时滞变换,将结果进一步推广到了含有控制时滞的情形。时变衰减幂次趋近律导出的滑模控制器能够保证系统状态最终收敛到原点,而不再是原点邻域中的某个稳态抖振。仿真结果表明了本文方法是有效的。本文方法还可以进一步推广到其他形式的离散系统,如离散广义系统等,具体结果尚待进一步研究。 [1]GaoWB,WangYF,HomaifAA.Discrete-timevariablestruc-turecontrolsystem[J].IEEETransactiononIndustrialElectronics, 1995, 42(2): 117-122. [2] 高为炳. 离散时间系统的变结构控制 [J]. 自动化学报, 1995, 21(2): 154-161. [3] 高为炳. 变结构控制理论与设计方法 [M]. 北京: 科学出版社, 1996, 278-300. [4]BartoszewiczA.Discrete-timequasi-sliding-modecontrolstrategies[J].IEEETransactionsonIndustrialElectronics, 1998, 45(4): 633-637. [5] 翟长连, 吴智铭. 一种离散时间系统的变结构控制方法 [J]. 上海交通大学学报, 2000, 34(5): 719-722. [6] 张益波, 张井岗, 陈志梅. 一种新的离散时间系统的变结构控制方法 [J]. 系统仿真学报, 2002, 14(11): 1524-1527. [7] 姚琼荟, 宋立忠, 温洪. 离散变结构系统的比例-等速-变速控制 [J]. 控制与决策, 2000, 15(3): 329-332. [8]XiaoYH,ZhouJL,GeZY,etal.Thereachinglawforvariablestructurecontrolofdiscretetimesystembasedonattenuatingcontrol[J].ControlTheoryandApplications, 2002, 19(3): 450-452. [9] 任启峰, 高存臣, 王品. 基于衰减控制的离散时间系统的变结构控制 [J]. 系统仿真学报, 2008, 20(4): 1056-1059. [10] 张新政, 邓则名, 高存臣. 滞后离散线性定常系统的准滑模变结构控制 [J]. 自动化学报, 2002, 28(4): 625-630. [11] 高存臣, 刘云龙, 李云艳. 不确定离散变结构控制系统的趋近律方法 [J]. 控制理论与应用, 2009, 26(7): 781-785. [12] 唐功友, 吕杉杉, 董瑞. 具有控制时滞的离散系统的无抖振滑模控制 [J]. 控制理论与应用, 2008, 25(6): 1045-1048. [13] 郑锋, 程勉, 高为炳. 控制存在时滞的系统的变结构控制 [J]. 控制与决策, 1993, 8(2): 95-100. [14] 李文林. 多输入离散时滞系统的保性能变结构控制 [J]. 系统仿真学报, 2008, 20(18): 4932-4936. 责任编辑 陈呈超 Variable Structure Control for Multi-Input Discrete Systems with Time-Delay in Control DENG Zhen1, CHEN Hong-Yan1, GAO Cun-Chen2 (1. School of General Education, Qingdao University of Technology, Qingdao 266300, China; 2. College of Mathematical Sciences, Ocean University of China, Qingdao 266100, China) The design method of variable structure control for multi-input discrete systems based on the time-varying attenuating power reaching law is proposed. This method is also extended to discrete systems with time-delay in control by a time-delay sate transform. Firstly, the gain matrix of linear switching function is chosen properly in order to assure that the poles of ideal quasi-sliding mode equation in quasi-switching manifold can be designed arbitrarily. Secondly, the quasi-sliding mode controller based on the time-varying attenuating power reaching law can ensure that the state trajectory of multi-input discrete systems with/without time-delay in control reaches a small neighborhood of quasi-switching manifold, and then the trajectory either arrives at the quasi-switching manifold in a next step or converges to the quasi-switching manifold quickly in a power exponential rate, the system state trajectory is guaranteed to converge into the origin of state space, not a stable chatting any more. Fainally a numerical simulation results demonstrate the proposed method is feasible and effective. discrete system; variable structure control; multi-input; time-delay; chattering 国家自然科学基金项目(60974025);青岛工学院2014年董事长基金项目(2014JY002)资助 2013-06-20; 2014-10-10 邓 臻(1977-),女,讲师。E-mail: dzh_52@163.com TP273 A 1672-5174(2015)04-130-05 10.16441/j.cnki.hdxb.20130269

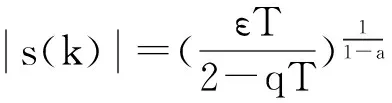
2 含控制时滞的多输入离散系统


3 仿真实例
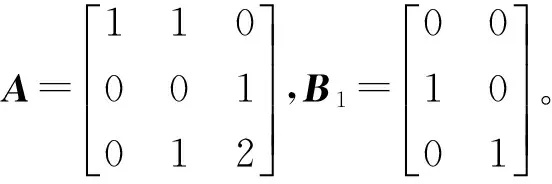



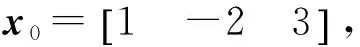






4 结语

