具有不同焊接孔的梁柱焊接节点非线性分析

陈雨

(同济大学建筑工程系，上海200092)

为了形成连续的梁上下翼缘对接焊缝，梁柱焊接节点通常需要在梁腹板进行切角(焊接孔)。然而，1994年美国Northridge地震和1995年日本Kobe地震出现大量梁柱焊接节点破坏事故，震害调查结果表明，部分梁柱焊接节点破坏发生在焊接孔处。一般认为，焊接孔处的破坏是由于焊接孔和梁翼缘相接处应力集中和焊接热影响使钢材韧性降低造成的。Nakashima等［1］对日本常用的梁柱焊接节点进行了试验研究，研究结果表明不同的焊接孔构造对节点延性影响较大，并提出了较为有利的焊接孔构造;El－Tawil［2］有限元分析结果表明，增加焊接孔的尺寸易于导致焊接孔与翼缘相接处延性断裂;Stojadinovic等［3］对十个梁柱焊接节点进行低周反复加载试验，发现几乎所有的试件破坏发生在焊接孔与梁翼缘相接处;Ricles等［4］对采用九种不同焊接孔的梁柱焊接节点进行了非线性有限元分析，得出较为合理的焊接孔构造，并进行了试验验证，该焊接孔被美国FEMA所采用。为了评估不同的焊接孔对节点延性的影响，本文分别选取中国建筑抗震设计规范推荐的焊接孔，Nakashima推荐的焊接孔和Ricles推荐的焊接孔，进行循环荷载作用下的非线性分析。

1 与本文有关的几个力学参数

延性断裂是结构钢在单调荷载作用下破坏的主要模式，细观力学认为钢材的延性断裂主要是由于金属中的微空洞引起的，金属材料在拉应力的作用下，引起微孔洞的形核和增长，最后微孔洞的结合形成宏观裂纹，材料发生破坏。Kanvinde等［5］提出了预测结构钢延性断裂的 VGI(Void Growth Index)模型和 SMCS(the Stress Modified Critical Strain)模型。

其中R是微孔洞当前时刻的直径;R0是初始时刻微孔洞的直径;σe是MISES等效应力，σm平均应力或静水压力称之为三轴比;ε是等效

P塑性应变，又称之为Mises塑性应变;dεP是增量形式的等效塑性应变，由下式定义:

当计算得到的满足下式时，即认为材料发生破坏。

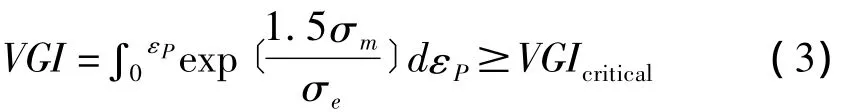
在单调比例加载且变形较小的情况下，可以认为三轴比在加载过程中保持不变，且与等效塑性应变保持独立，可以得到SMCS模型:

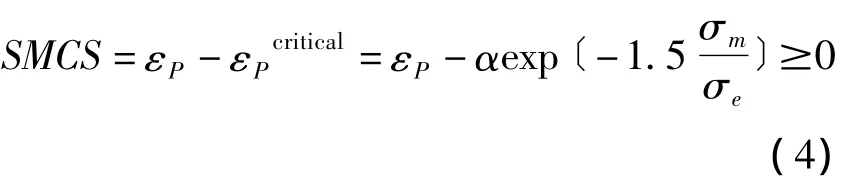
其中VGIcritical和α为材料韧性参数，通过带圆弧槽口的拉杆试验结合有限元分析确定。

虽然VGI模型和SMCS模型可以较准确地预测结构钢的延性断裂，但是应用该模型需要把有限元模型的单元尺寸设定为0.1 mm的量级，由于目前的计算机性能有限，应用该模型分析实际的大型结构构件仍然非常困难。

根据(4)式，本文定义断裂指数RI(Rupture Index):

可见，在一定的加载条件下，断裂指数越大的构件越接近延性断裂 ，在位移控制的单调荷载作用下所能够达到的最大位移越小，延性越差，因此可以应用断裂指数RI来评估结构或构件的相对延性。

本文应用断裂指数RI和等效塑性应变来评估具有不同焊接孔的节点在单调荷载作用下的延性。同时，本文应用纵向塑性应变时程曲线和累积塑性应变来评估节点在循环荷载作用下的延性，Kanvinde等认为累积塑性应变显著降低了材料的韧性参数。

2 有限元模型的校核

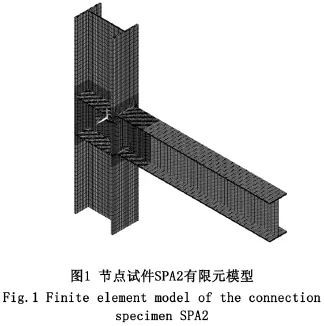
本文有限元模型选取文献［6］中梁柱焊接节点试件，试件梁截面为 H400200812，柱截面为H4503001216，钢材为Q235钢。本文有限元模型包括梁上下翼缘对接焊缝，梁腹板角焊缝和焊接孔等细节，有限元模型选取SOLID185单元，钢材和焊缝金属的弹性模量均取200 GPa，泊松比0.3，钢材的屈服强度取300 MPa，焊缝金属的屈服强度取370 MPa，有限元模型如图1所示。通过采用大位移小应变分析来考虑几何非线性的影响。加载等级采用与试验相同的加载等级，试验得到的荷载－位移曲线与计算得到的荷载－位移曲线如图2、图3所示。可见，计算曲线与试验曲线相近，证明了有限元模型的可靠性。

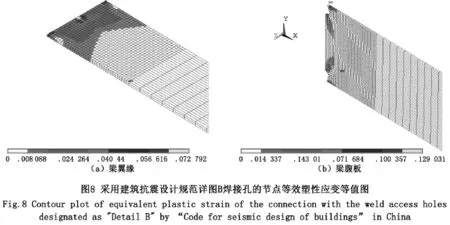
本文应用通用有限元软件ANSYS，采用等幅加载，加载位移幅为±45 mm(约3倍的节点屈服位移)，进行循环荷载作用下的几何非线性和材料非线性分析，共循环7周。其中第一荷载步视为单调荷载，读取第一荷载步的分析结果，以判断不同构造的焊接孔附近抵抗延性断裂的性能。应用循环荷载作用下的分析结果，从而判断不同构造的焊接孔抵抗低周疲劳破坏的性能。在单调荷载作用下，采用中国建筑抗震设计规范推荐的焊接孔有限元模型MISES塑性应变等值图如图7和图8所示。可见，采用中国建筑抗震设计规范推荐的焊接孔根部等效塑性应变较大。

3 有限元分析

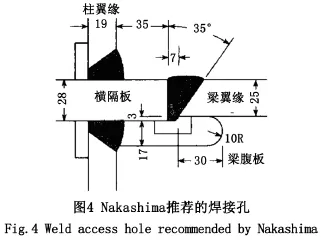
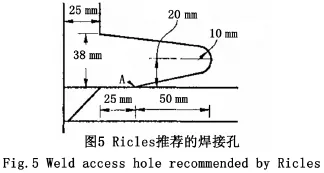
为了分析比较不同的焊接孔所造成的应力集中程度，本文焊接孔分别选取Nakashima焊接孔(图4所示)、Ricles焊接孔(图5所示)和中国建筑抗震设计规范推荐的焊接孔(图6所示)。

读取第一荷载步梁受拉翼缘焊接孔根部应力集中区的分析结果，包括等效塑性应变、静水压力和MISES等效应力，计算各焊接孔根部附近的最大等效塑性应变，最大三轴比和最大断裂指数RI，分别列于图9～图11。可见，采用中国建筑抗震设计规范推荐的焊接孔详图A和详图B根部应力集中区均产生较大的等效塑性应变。根据图8(a)可以判断，详图B焊接孔根部所产生的应力集中区恰位于对接焊缝处的热影响区，热影响区通常具有相对最低的断裂韧性，易导致节点在该应力集中区首先发生破坏。清华大学熊俊对9个节点试件进行了低周反复加载试验，其中8个节点试件破坏首先在该焊接孔根部应力集中区，所有节点试件均表现较差的延性，本文的分析结果很好地解释了这一破坏现象。

Nakashima推荐的焊接孔和Ricles推荐的焊接孔具有较大的三轴比，其中Nakashima推荐的焊接孔具有较大的断裂指数，抵抗延性断裂的性能较差，Ricles推荐的焊接孔和中国建筑抗震设计规范推荐的焊接孔具有相近的断裂指数。

读取最后荷载步的分析结果，得出各焊接孔根部附近最大的累积塑性应变如图12所示。中国建筑抗震设计规范推荐的焊接孔具有相对较大的累积塑性应变，而Ricles推荐的焊接孔的焊接孔根部应力集中区所产生的累积塑性应变最小，具有相对较好的抵抗低周疲劳破坏的性能。Nakashima推荐的焊接孔根部同样产生较大的应力集中，也同样具有较大的累积塑性应变，且具有相对最高的断裂指数，因此本文认为也不宜采用。

4 既有试验验证

清华大学熊俊［7］对9个T形单侧节点进行了试验研究，所有试件的焊接孔均分别采用中国建筑抗震设计规范推荐的焊接孔详图A和详图B，钢材材质为Q345。所有试件破坏均首先发生在焊接孔附近的应力集中区，其中8个试件首先破坏在焊接孔详图B根部附近的应力集中区，然后焊接孔详图A应力集中区也开始开裂;另一个试件首先在焊接孔详图A处开裂，然后焊接孔详图B处也开始出现裂纹，所有节点试件均表现较差的延性。

日本的Rahiminia［8］对14个节点试件进行了反复加载试验研究，其中12个试件均采用日本常用的焊接孔(类似于中国建筑抗震设计规范推荐的焊接孔详图A)，2个试件采用图4所示焊接孔。所有试件均首先破坏在焊接孔处。

Ricles［4］对11个采用图2所示焊接孔的梁柱焊接节点进行低周反复加载试验，其中6个试件为T形单侧节点，5个试件为十字形节点。所有试件均没有在焊接孔处发生破坏。

Nakashima［1］对6 个采用日本常用焊接孔(相近于中国建筑抗震设计规范焊接孔详图A)的试件和4个采用图4所示焊接孔的梁柱焊接节点进行了动力加载和准静态加载试验，其中采用图4所示焊接孔的4个试件在焊接孔处均没有出现破坏，且与采用其它构造形式的焊接孔相比，4个试件具有较好的延性;而6个采用日本常用焊接孔的试件在试验中出现起始于焊接孔处的裂纹。

以上试验结果证明了本文有限元分析的正确性。

5 结论

有限元分析证明:不同的焊接孔的外形和尺寸对节点延性具有重要的影响，容易导致节点在焊接孔根部应力集中区提前破坏，从而显著影响节点延性。

不同构造的焊接孔根部所产生的应力集中程度不同，从而对节点延性具有不同的影响。本文的分析结果证明了中国建筑抗震规范推荐的焊接孔在应力集中区产生的塑性应变稍大，而Nakashima推荐的焊接孔也同样具有较高的应力集中，不宜采用。

美国Ricles推荐的焊接孔根部应力集中程度相对较小。需要指出的是，Ricles推荐的焊接孔在焊接孔与梁翼缘相接处具有较高的三轴比，其值约为1.42，但该处等效塑性应变较小，仅为0.038。损伤力学认为高三轴比使材料变脆，对单调荷载作用下的延性断裂极为不利。

［1］MASAYOSHI NAKASHIMA，KEIICHIRO SUITA，KIYOTAKA MORISAKO.Test of welded beam －column subassemblies.I:Global behavior［J］.Journal of Structure Engineering，1998，124(11):1236 －1244.

［2］SHERIF EL TAWIL，TAMEKA MIKESELL，SASHI K，et al.Effect of local details and yield ratio on behavior of fully restrained steel connections［J］.Journal of Structural Engineering，1999，125(1):79 －87.

［3］STOJADINOVIC B，GOEL S C，LEE K，et al.Parametric tests on steel moment connections［J］.Journal of Structural Engineering，2000，126(1):40 －49.

［4］CHANGSHI MAO，JAMES RICLES，LE WU LU，et al.Effect of local details on ductility of welded moment connections［J］.Journal of Structural Engineering，2001，127(9):1036－1044.

［5］KANVINDE A M，DEIERLEIN G G.Void growth model and stress modified critical strain model to predict ductile fracture in structural steels［J］.Journal of Structure Engineering，2006，132(2):1907 －1918.

［6］茹继平.梁腹板开圆孔节点及钢框架抗震性能的实验研究［D］.北京:北京交通大学，2005.

［7］熊俊.强震作用下钢框架焊接节点损伤性能和计算模型研究［D］.北京:清华大学，2011.

［8］FARAMARZ RAHIMINIA.Effects of joints panel shear deformation on elasto－plastic behavior of steel beam－to－ column connections［D］.Kobe:Kobe University，2013.