徐州市城市生活垃圾产生量预测分析

董 兵，刘汉湖，李 凯，杨泰宇

（1.中国矿业大学环境与测绘学院，江苏 徐州 221116；2.江苏省资源环境信息工程重点实验室（中国矿业大学），江苏 徐州 221116）

城市生活垃圾产生量预测方法一般可分为2类：一类是定性预测法，主要依靠调查研究与经验判断；另一类是定量预测法，依据统计数据，建立数学模型，这类预测由于有较强的理论基础支撑，一般准确性较好，应用较广。常用的数学模型有灰色预测模型、多元回归模型、逐步回归模型、时间序列分析法等［1］。笔者选取徐州市为研究对象，通过对徐州市的城市生活垃圾进行调查分析，以徐州市1999—2008年的数据（城市生活垃圾产生量、常住人口数量、GDP、人均可支配收入、固定投资）为基础，通过Matlab软件建立灰色预测模型和多元线性回归模型，对徐州市未来城市生活垃圾产生量进行预测，为类似的城市提供类比参考依据。

1 预测指标与基础数据

1.1 徐州市城市生活垃圾产生量概况

依据徐州市统计年鉴，徐州市1999—2008年城市生活垃圾产生量及增长率如表1所示。

徐州市城市生活垃圾产生量总体上呈逐年增长趋势，个别年份出现下降现象，这也是经济发展、居民生活水平提高的侧面表现。但城市生活垃圾的年增长率总体呈下降趋势，这正是人们环境健康意识提高、环境管理体系改善的体现。综合来讲，就是城市扩建和经济发展在提高居民生活质量的同时，给城市生活垃圾的清运带来了巨大的压力，而城市生活垃圾的处理不当又会对居民的健康产生极大危害，所以城市生活垃圾的产生量以及处理情况愈来愈受到人们的关注和重视。

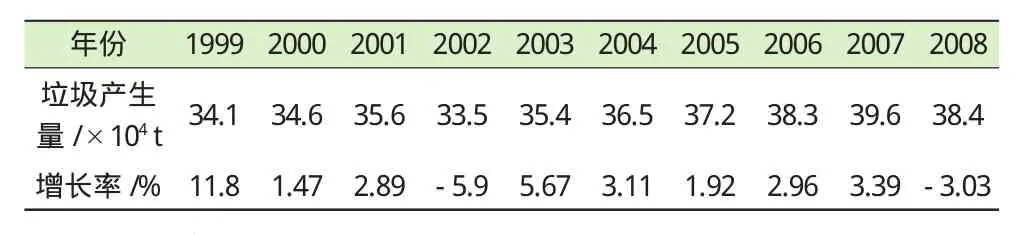
表1 1999—2008年徐州市城市生活垃圾产生量

1.2 影响因素分析

城市生活垃圾产生量的影响因素众多，但主要表现为以下3个方面：人口、社会经济发展水平和居民生活水平［2-3］，同时考虑到历年数据的完整性，以及数据的可获取性，选取了人口、GDP、人均可支配收入以及固定投资等4个因素作为城市生活垃圾产生量的影响因素。1999—2008年徐州市城市生活垃圾影响因素统计见表2。

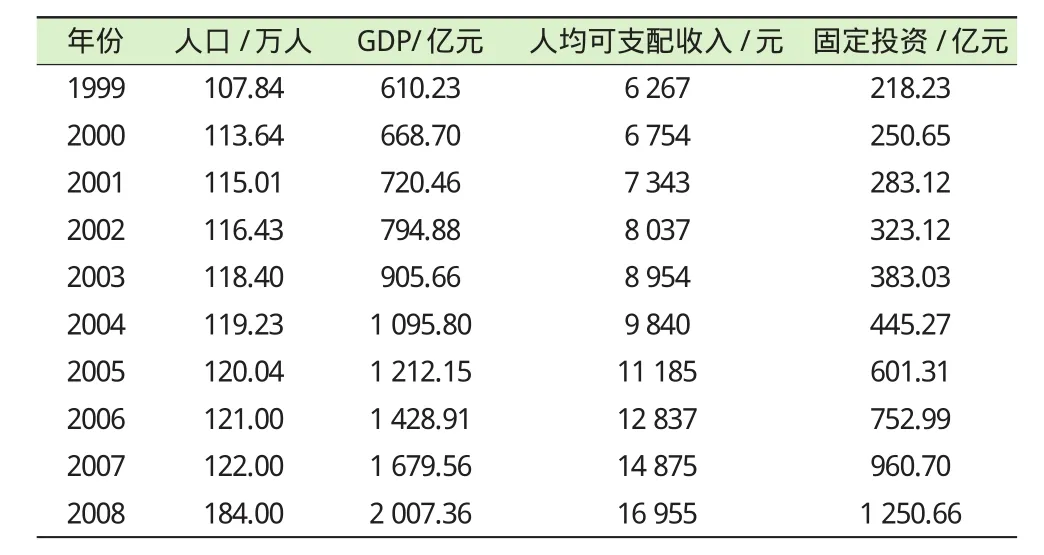
表2 徐州市城市生活垃圾产生量的影响因素

2 灰色GM（1,1） 预测

城市垃圾系统既有已知信息，也有未知信息，它是本征性灰色系统，符合灰色理论的建模条件［4-5］。因此选择灰色预测法中灰色时间序列预测模型来预测城市生活垃圾产生量。

城市生活垃圾产生量预测步骤如下。

第1步：级比检验。

建立垃圾产生量数据时间序列如下：

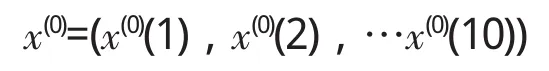
计算级比h(k)=x(0)(k-1)/x(0)(k)

经过级比判断，x(0)可使用GM（1，1） 建模。

第2步：建立GM（1，1） 模型。

通过对原始数据（表1） 进行累加及构造数据矩阵B和数据向量Y，建立模型，并通过Matlab软件求得相关参数a=-0.017 7，u=33.132 7，进而解得预测模型：

各年度的拟合值见表3。

表3 1999—2008年拟合数据及精度检验

将分析模型的预测结果与原始值进行对比，计算得出相对误差均在5%的范围内，且平均相对误差为1.69%，证明该模型的预测比较合理。可以用来对徐州市未来的城市生活垃圾产生量进行预测，特别适用于很多因素不确定的情况。徐州市2009—2018年城市生活垃圾产生量预测值见表4。

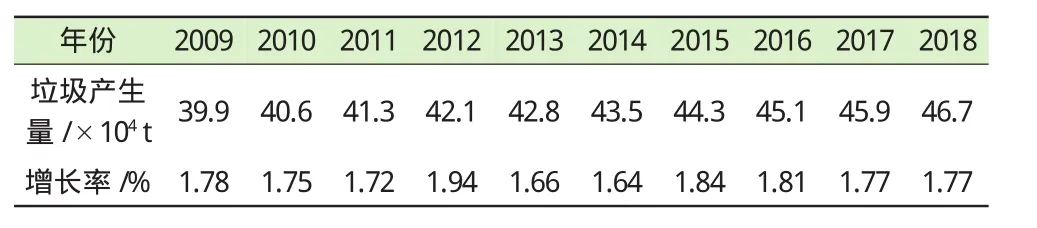
表4 2009—2018年徐州市城市生活垃圾产生量预测结果

由于上述预测是依据现有数据和目前管理现状所提出的，如果加强管理、采取相关措施或是与生活垃圾产生量相关的社会、自然、经济等因素发生大的波动，上述预测数据的可信度将会大幅降低。所以在此基础上，考虑城市生活垃圾产生量的一些主要影响因素，搜集相关数据，运用多元线性回归模型对徐州市城市生活垃圾产生量进行预测。

3 多元线性回归方法

应用多元线性回归分析法能够较综合地、全面地反映出生活垃圾产生量与各内在因素之间的关系，进而能够较准确地预测出生活垃圾的产生量［6］。

3.1 模型的建立

多元线性回归预测模型的建立是在上述影响因子确定后，选取1999—2008年的各因变量与自变量的已有数据（表1～2），代入到四元线性回归方程中，根据最小二乘法原理，用Matlab拟合估计得到回归系数，进而求得四元线性回归方程参数的标准方程。通过对方程进行参数检验以及实证分析，确定该预测模型是否适用，若适用，则建立预测模型［7-8］。方程的回归系数如表5所示。

表5 回归方程的系数及置信区间

由Matlab软件进行线性回归分析，可知方程的估计参数系数a均在95%置信区间内，由此得到多元线性回归方程：

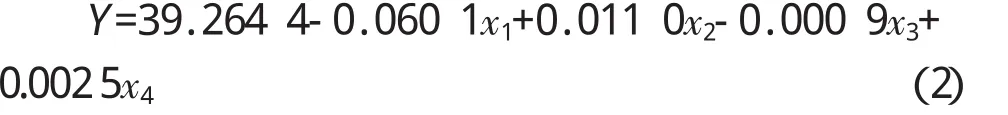
检验回归模型的相关参数见表6。

表6 回归方程的相关参数

相关系数R2=0.919 1表明自变量与因变量之间呈高度正相关；F＝14.204 1＞F0.05（4,5） =5.19；概率P=0.0061＜0.05，可知该回归模型成立。

通过残差分析得出，除第4个数据外其余数据的残差离零点均较近，且残差的置信区间均包含零点，这也说明了回归模型能较好地拟合原始数据，而第4个数据可视为异常点。

3.2 模型的检验

以徐州市1999—2008年的数据为训练样本，2009—2010年的数据作为测试样本检验预测模型的可靠性和准确性。结果如表7所示。

表7 1999—2010年徐州市城市生活垃圾产生量预测结果

将分析模型的预测结果与检验指标进行对比，训练样本与测试样本的相对误差均在5%的范围内，且平均相对误差为1.52%，证明该模型的预测比较合理，可以用来对徐州市未来的城市生活垃圾产生量进行预测。

3.3 徐州市生活垃圾产生量的预测

3.3.1 各影响因素的取值方法

按照年增长率1.13%计算未来几年徐州市区常住人口数，根据徐州市“十二五”规划可知固定投资按年均增长率为13.8%，因此固定投资按年增长率13.8%进行预测，徐州市GDP和人均可支配收入拟采用直线拟合和指数拟合2种方式，结果见表8，R2越接近1，表明拟合效果越好，因此采用指数拟合的方式进行预测。

表8 人均可支配收入和GDP的拟合公式

3.3.2 产生量预测

在对生活垃圾产生量的4个主要影响因素作出预测的基础上，利用公式（2） 对徐州市2009—2018年的城市生活垃圾产生量进行了预测。得出2009—2018年徐州市生活垃圾产生量分别为：4.15×105、3.86×105、4.06×105、4.12×105、4.20×105、4.30×105、4.42×105、4.56×105、4.61×105、4.73×105t。

4 结论

在分析了徐州市1999—2008年城市生活垃圾产生量与主要影响因素的基础上，建立了GM（1,1）模型和多元线性回归模型，得到以下主要结论。

1）建立了徐州市城市生活垃圾灰色预测GM（1,1） 模型，模型为

2)考虑人口、GDP、人均可支配收入以及固定投资4个因素，建立了预测徐州市生活垃圾产生量的多元线性回归模型：Y=39.2644-0.0601x1+0.0110x2-0.000 9x3+0.002 5x4。

通过检验，自变量与因变量的相关系数R2=0.919 1，自变量与因变量之间相关性较好，说明了该多元线性回归模型具有实用价值。

3）通过对2种预测方法的预测结果（表4、表7）进行比较分析，得出2种模型的预测结果相近，没有出现较大的偏差，这也说明了1999—2010年徐州市与城市生活垃圾相关联的社会、自然以及经济因素并未发生大的波动；但2011—2018年2种模型的垃圾产生量预测值出现了些许的偏差，多元线性回归模型的预测值稍高于GM（1,1）模型的预测值，比较而言多元线性回归模型更精确些，由于2种模型的偏差不是很大，所以在特殊（某些影响因素数据缺失）情况下，也可以使用灰色GM（1,1）预测法对徐州市的生活垃圾产生量做粗略预测。

4）总体观察，可以发现虽然整体上徐州市城市生活垃圾产生量呈逐年增长趋势，但其增长趋势趋缓。

［1］姚颖悟.我国城市垃圾处理现状与分析［J］.环境保护科学，2004，30（2）：37-39.

［2］向盛斌.城市居民生活垃圾影响因素分析及产量预测［J］.环境卫生工程，1998，6（1）：7-12.

［3］梁广生.北京市2002—2007年城市生活垃圾产量预测分析［J］.环境科学研究，2003，16（5）：48-51.

［4］Chen H W，Chang N B.Prediction analysis or solid waste generation basedd on grey fuzzy dynamic modeling［J］.Resour Conserv Recycl，2000，29：1-18.

［5］邓聚龙.灰理论基础［M］.武汉：华中科技大学出版社，2002.

［6］旦增，彭鹏，谭均，等.多元线性回归模型在拉萨市区城市生活垃圾产量预测中的应用［J］.西藏科技，2013（8）：40-42.

［7］宣明.数学建模与数学实验［M］.杭州：浙江大学出版社，2010.

［8］何正风.MATLAB在数学方面的应用［M］.北京：清华大学出版社，2005.